ga

Find minimum of function using genetic algorithm

collapse all in page

Syntax

x = ga(fun,nvars)

x = ga(fun,nvars,A,b)

x = ga(fun,nvars,A,b,Aeq,beq)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,options)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,intcon)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,intcon,options)

x = ga(problem)

[x,fval]
= ga(___)

[x,fval,exitflag,output]
= ga(___)

[x,fval,exitflag,output,population,scores]
= ga(___)

Description

x = ga(fun,nvars) finds a local unconstrained minimum, x, to the objective function, fun. nvars is the dimension (number of design variables) of fun.

Note

Passing Extra Parameters explains how to pass extra parameters to the objective function and nonlinear constraint functions, if necessary.

example

x = ga(fun,nvars,A,b) finds a local minimum x to fun, subject to the linear inequalities A*x ≤ b. ga evaluates the matrix product A*x as if x is transposed (A*x').

example

x = ga(fun,nvars,A,b,Aeq,beq) finds a local minimum x to fun, subject to the linear equalities Aeq*x = beq and A*x ≤ b. (Set A=[] and b=[] if no linear inequalities exist.) ga evaluates the matrix product Aeq*x as if x is transposed (Aeq*x').

example

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub) defines a set of lower and upper bounds on the design variables, x, so that a solution is found in the range lb ≤ x ≤ ub. (Set Aeq=[] and beq=[] if no linear equalities exist.)

example

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon) subjects the minimization to the constraints defined in nonlcon. The function nonlcon accepts x and returns vectors C and Ceq, representing the nonlinear inequalities and equalities respectively. ga minimizes the fun such that C(x) ≤ 0 and Ceq(x) = 0. (Set lb=[] and ub=[] if no bounds exist.)

example

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,options) minimizes with the default optimization parameters replaced by values in options. (Set nonlcon=[] if no nonlinear constraints exist.) Create options using optimoptions.

example

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,intcon) or x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,intcon,options) requires that the variables listed in intcon take integer values.

Note

When there are integer constraints, ga does not accept nonlinear equality constraints, only nonlinear inequality constraints.

example

x = ga(problem) finds the minimum for problem, a structure described in problem.

[x,fval] = ga(___), for any previous input arguments, also returns fval, the value of the fitness function at x.

example

[x,fval,exitflag,output] = ga(___) also returns exitflag, an integer identifying the reason the algorithm terminated, and output, a structure that contains output from each generation and other information about the performance of the algorithm.

example

[x,fval,exitflag,output,population,scores] = ga(___) also returns a matrix population, whose rows are the final population, and a vector scores, the scores of the final population.

example

Examples

collapse all

Optimize a Nonsmooth Function Using `ga`

Open Live Script

The ps_example.m file is included when you run this example. Plot the function.

xi = linspace(-6,2,300);
yi = linspace(-4,4,300);
[X,Y] = meshgrid(xi,yi);
Z = ps_example([X(:),Y(:)]);
Z = reshape(Z,size(X));
surf(X,Y,Z,'MeshStyle','none')
colormap 'jet'
view(-26,43)
xlabel('x(1)')
ylabel('x(2)')
title('ps\_example(x)')

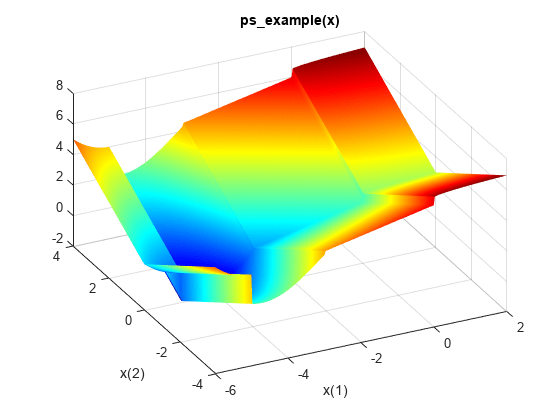
Figure contains an axes object. The axes object with title ps_example(x), xlabel x(1), ylabel x(2) contains an object of type surface.

Find the minimum of this function using ga.

rng default % For reproducibility
x = ga(@ps_example,2)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

x = 1×2

   -4.6793   -0.0860

Minimize a Nonsmooth Function with Linear Constraints

Open Live Script

Use the genetic algorithm to minimize the ps_example function on the region x(1) + x(2) >= 1 and x(2) <= 5 + x(1). This function is included when you run this example.

First, convert the two inequality constraints to the matrix form A*x <= b. In other words, get the x variables on the left-hand side of the inequality, and make both inequalities less than or equal:

-x(1) -x(2) <= -1

-x(1) + x(2) <= 5

A = [-1,-1;
    -1,1];
b = [-1;5];

Solve the constrained problem using ga.

rng default % For reproducibility
fun = @ps_example;
x = ga(fun,2,A,b)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

x = 1×2

    0.9990    0.0000

The constraints are satisfied to within the default value of the constraint tolerance, 1e-3. To see this, compute A*x' - b, which should have negative components.

disp(A*x' - b)

    0.0010
   -5.9990

Minimize a Nonsmooth Function with Linear Equality and Inequality Constraints

Open Live Script

Use the genetic algorithm to minimize the ps_example function on the region x(1) + x(2) >= 1 and x(2) == 5 + x(1). This function is included when you run this example.

First, convert the two constraints to the matrix form A*x <= b and Aeq*x = beq. In other words, get the x variables on the left-hand side of the expressions, and make the inequality into less than or equal form:

-x(1) -x(2) <= -1

-x(1) + x(2) == 5

A = [-1 -1];
b = -1;
Aeq = [-1 1];
beq = 5;

Solve the constrained problem using ga.

rng default % For reproducibility
fun = @ps_example;
x = ga(fun,2,A,b,Aeq,beq)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

x = 1×2

   -2.0005    2.9995

Check that the constraints are satisfied to within the default value of ConstraintTolerance, 1e-3.

disp(A*x' - b)

   1.0000e-03

disp(Aeq*x' - beq)

   8.5897e-09

Optimize with Linear Constraints and Bounds

Open Live Script

Use the genetic algorithm to minimize the ps_example function on the region x(1) + x(2) >= 1 and x(2) == 5 + x(1). The ps_example function is included when you run this example. In addition, set bounds 1 <= x(1) <= 6 and -3 <= x(2) <= 8.

First, convert the two linear constraints to the matrix form A*x <= b and Aeq*x = beq. In other words, get the x variables on the left-hand side of the expressions, and make the inequality into less than or equal form:

-x(1) -x(2) <= -1

-x(1) + x(2) == 5

A = [-1 -1];
b = -1;
Aeq = [-1 1];
beq = 5;

Set bounds lb and ub.

lb = [1 -3];
ub = [6 8];

Solve the constrained problem using ga.

rng default % For reproducibility
fun = @ps_example;
x = ga(fun,2,A,b,Aeq,beq,lb,ub)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

x = 1×2

    1.0000    6.0000

Check that the linear constraints are satisfied to within the default value of ConstraintTolerance, 1e-3.

disp(A*x' - b)

   -6.0000

disp(Aeq*x' - beq)

  -7.9765e-08

Optimize with Nonlinear Constraints Using `ga`

Open Live Script

Use the genetic algorithm to minimize the ps_example function on the region $2 x_{1}^{2} + x_{2}^{2} \leq 3$ and $(x_{1} + 1)^{2} = (x_{2} / 2)^{4}$ . The ps_example function is included when you run this example.

To do so, use the function ellipsecons.m that returns the inequality constraint in the first output, c, and the equality constraint in the second output, ceq. The ellipsecons function is included when you run this example. Examine the ellipsecons code.

type ellipsecons

function [c,ceq] = ellipsecons(x)

c = 2*x(1)^2 + x(2)^2 - 3;
ceq = (x(1)+1)^2 - (x(2)/2)^4;

Include a function handle to ellipsecons as the nonlcon argument.

nonlcon = @ellipsecons;
fun = @ps_example;
rng default % For reproducibility
x = ga(fun,2,[],[],[],[],[],[],nonlcon)

Optimization finished: average change in the fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.

x = 1×2

   -0.9766    0.0362

Check that the nonlinear constraints are satisfied at x. The constraints are satisfied when c ≤ 0 and ceq = 0 to within the default value of ConstraintTolerance, 1e-3.

[c,ceq] = nonlcon(x)

c = 
-1.0911

ceq = 
5.4645e-04

Minimize with Nondefault Options

Open Live Script

Use the genetic algorithm to minimize the ps_example function on the region x(1) + x(2) >= 1 and x(2) == 5 + x(1) using a constraint tolerance that is smaller than the default. The ps_example function is included when you run this example.

-x(1) -x(2) <= -1

-x(1) + x(2) == 5

A = [-1 -1];
b = -1;
Aeq = [-1 1];
beq = 5;

To obtain a more accurate solution, set a constraint tolerance of 1e-6. And to monitor the solver progress, set a plot function.

options = optimoptions('ga','ConstraintTolerance',1e-6,'PlotFcn', @gaplotbestf);

Solve the minimization problem.

rng default % For reproducibility
fun = @ps_example;
x = ga(fun,2,A,b,Aeq,beq,[],[],[],options)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

Figure Genetic Algorithm contains an axes object. The axes object with title Best: 4 Mean: 4, xlabel Generation, ylabel Fitness value contains 2 objects of type scatter. These objects represent Best fitness, Mean fitness.

x = 1×2

   -2.0000    3.0000

Check that the linear constraints are satisfied to within 1e-6.

disp(A*x' - b)

   9.9809e-07

disp(Aeq*x' - beq)

  -7.3589e-08

Minimize a Nonlinear Function with Integer Constraints

Open Live Script

Use the genetic algorithm to minimize the ps_example function subject to the constraint that x(1) is an integer. This function is included when you run this example.

intcon = 1;
rng default % For reproducibility
fun = @ps_example;
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = [];
x = ga(fun,2,A,b,Aeq,beq,lb,ub,nonlcon,intcon)

ga stopped because the average change in the penalty function value is less than options.FunctionTolerance and 
the constraint violation is less than options.ConstraintTolerance.

x = 1×2

   -5.0000   -0.0834

Obtain the Solution and Function Value

Open Live Script

Use the genetic algorithm to minimize an integer-constrained nonlinear problem. Obtain both the location of the minimum and the minimum function value. The objective function, ps_example, is included when you run this example.

intcon = 1;
rng default % For reproducibility
fun = @ps_example;
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = [];
[x,fval] = ga(fun,2,A,b,Aeq,beq,lb,ub,nonlcon,intcon)

ga stopped because the average change in the penalty function value is less than options.FunctionTolerance and 
the constraint violation is less than options.ConstraintTolerance.

x = 1×2

   -5.0000   -0.0834

fval = 
-1.8344

Compare this result to the solution of the problem with no constraints.

[x,fval] = ga(fun,2)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

x = 1×2

   -4.6906   -0.0078

fval = 
-1.9918

Obtain Diagnostic Information

Open Live Script

Use the genetic algorithm to minimize the ps_example function constrained to have x(1) integer-valued. The ps_example function is included when you run this example. To understand the reason the solver stopped and how ga searched for a minimum, obtain the exitflag and output results. Also, plot the minimum observed objective function value as the solver progresses.

intcon = 1;
rng default % For reproducibility
fun = @ps_example;
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = [];
options = optimoptions('ga','PlotFcn', @gaplotbestf);
[x,fval,exitflag,output] = ga(fun,2,A,b,Aeq,beq,lb,ub,nonlcon,intcon,options)

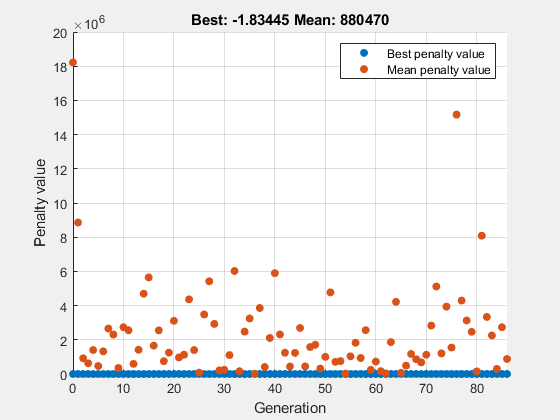
Figure Genetic Algorithm contains an axes object. The axes object with title Best: -1.83445 Mean: 880470, xlabel Generation, ylabel Penalty value contains 2 objects of type scatter. These objects represent Best penalty value, Mean penalty value.

ga stopped because the average change in the penalty function value is less than options.FunctionTolerance and 
the constraint violation is less than options.ConstraintTolerance.

x = 1×2

   -5.0000   -0.0834

fval = 
-1.8344

exitflag = 
1

output = struct with fields:
      problemtype: 'integerconstraints'
         rngstate: [1x1 struct]
      generations: 86
        funccount: 3311
          message: 'ga stopped because the average change in the penalty function value is less than options.FunctionTolerance and ...'
    maxconstraint: 0
       hybridflag: []

Obtain Final Population and Scores

Open Live Script

Use the genetic algorithm to minimize the ps_example function constrained to have x(1) integer-valued. The ps_example function is included when you run this example. Obtain all outputs, including the final population and vector of scores.

intcon = 1;
rng default % For reproducibility
fun = @ps_example;
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = [];
[x,fval,exitflag,output,population,scores] = ga(fun,2,A,b,Aeq,beq,lb,ub,nonlcon,intcon);

ga stopped because the average change in the penalty function value is less than options.FunctionTolerance and 
the constraint violation is less than options.ConstraintTolerance.

Examine the first 10 members of the final population and their corresponding scores. Notice that x(1) is integer-valued for all these population members. The integer ga algorithm generates only integer-feasible populations.

disp(population(1:10,:))

   1.0e+03 *

   -0.0050   -0.0001
   -0.0050   -0.0001
   -1.6420    0.0027
   -1.5070    0.0010
   -0.4540    0.0104
   -0.2530   -0.0011
   -0.1210   -0.0003
   -0.1040    0.1314
   -0.0140   -0.0010
    0.0160   -0.0002

disp(scores(1:10))

Input Arguments

collapse all

`fun` — Objective function
function handle | function name

Objective function, specified as a function handle or function name. Write the objective function to accept a row vector of length nvars and return a scalar value.

When the 'UseVectorized' option is true, write fun to accept a pop-by-nvars matrix, where pop is the current population size. In this case, fun returns a vector the same length as pop containing the fitness function values. Ensure that fun does not assume any particular size for pop, since ga can pass a single member of a population even in a vectorized calculation.

Example: fun = @(x)(x-[4,2]).^2

Data Types: char | function_handle | string

`nvars` — Number of variables
positive integer

Number of variables, specified as a positive integer. The solver passes row vectors of length nvars to fun.

Example: 4

Data Types: double

`A` — Linear inequality constraints
real matrix

Linear inequality constraints, specified as a real matrix. A is an M-by-nvars matrix, where M is the number of inequalities.

A encodes the M linear inequalities

A*x <= b,

where x is the column vector of nvars variables x(:), and b is a column vector with M elements.

For example, to specify

x₁ + 2x₂ ≤ 10
3x₁ + 4x₂ ≤ 20
5x₁ + 6x₂ ≤ 30,

give these constraints:

A = [1,2;3,4;5,6];
b = [10;20;30];

Example: To specify that the control variables sum to 1 or less, give the constraints A = ones(1,N) and b = 1.

Data Types: double

`b` — Linear inequality constraints
real vector

Linear inequality constraints, specified as a real vector. b is an M-element vector related to the A matrix. If you pass b as a row vector, solvers internally convert b to the column vector b(:).

b encodes the M linear inequalities

A*x <= b,

where x is the column vector of N variables x(:), and A is a matrix of size M-by-N.

For example, to specify

x₁ + 2x₂ ≤ 10
3x₁ + 4x₂ ≤ 20
5x₁ + 6x₂ ≤ 30,

give these constraints:

A = [1,2;3,4;5,6];
b = [10;20;30];

Example: To specify that the control variables sum to 1 or less, give the constraints A = ones(1,N) and b = 1.

Data Types: double

`Aeq` — Linear equality constraints
real matrix

Linear equality constraints, specified as a real matrix. Aeq is an Me-by-nvars matrix, where Me is the number of equalities.

Aeq encodes the Me linear equalities

Aeq*x = beq,

where x is the column vector of N variables x(:), and beq is a column vector with Me elements.

For example, to specify

x₁ + 2x₂ + 3x₃ = 10
2x₁ + 4x₂ + x₃ = 20,

give these constraints:

Aeq = [1,2,3;2,4,1];
beq = [10;20];

Example: To specify that the control variables sum to 1, give the constraints Aeq = ones(1,N) and beq = 1.

Data Types: double

`beq` — Linear equality constraints
real vector

Linear equality constraints, specified as a real vector. beq is an Me-element vector related to the Aeq matrix. If you pass beq as a row vector, solvers internally convert beq to the column vector beq(:).

beq encodes the Me linear equalities

Aeq*x = beq,

where x is the column vector of N variables x(:), and Aeq is a matrix of size Meq-by-N.

For example, to specify

x₁ + 2x₂ + 3x₃ = 10
2x₁ + 4x₂ + x₃ = 20,

give these constraints:

Aeq = [1,2,3;2,4,1];
beq = [10;20];

Example: To specify that the control variables sum to 1, give the constraints Aeq = ones(1,N) and beq = 1.

Data Types: double

`lb` — Lower bounds
`[]` (default) | real vector or array

Lower bounds, specified as a real vector or array of doubles. lb represents the lower bounds element-wise in lb ≤ x ≤ ub.

Internally, ga converts an array lb to the vector lb(:).

Example: lb = [0;-Inf;4] means x(1) ≥ 0, x(3) ≥ 4.

Data Types: double

`ub` — Upper bounds
`[]` (default) | real vector or array

Upper bounds, specified as a real vector or array of doubles. ub represents the upper bounds element-wise in lb ≤ x ≤ ub.

Internally, ga converts an array ub to the vector ub(:).

Example: ub = [Inf;4;10] means x(2) ≤ 4, x(3) ≤ 10.

Data Types: double

`nonlcon` — Nonlinear constraints
function handle | function name

Nonlinear constraints, specified as a function handle or function name. nonlcon is a function that accepts a vector or array x and returns two arrays, c(x) and ceq(x).

c(x) is the array of nonlinear inequality constraints at x. ga attempts to satisfy
c(x) <= 0
for all entries of c.
ceq(x) is the array of nonlinear equality constraints at x. ga attempts to satisfy
ceq(x) = 0
for all entries of ceq.

For example,

x = ga(@myfun,4,A,b,Aeq,beq,lb,ub,@mycon)

where mycon is a MATLAB^® function such as

function [c,ceq] = mycon(x)
c = ...     % Compute nonlinear inequalities at x.
ceq = ...   % Compute nonlinear equalities at x.

For more information, see Nonlinear Constraints.

To learn how to use vectorized constraints, see Vectorized Constraints.

Note

ga does not enforce nonlinear constraints to be satisfied when the PopulationType option is set to 'bitString' or 'custom'.

If intcon is not empty, the second output of nonlcon (ceq) must be an empty entry ([]).

For information on how ga uses nonlcon, see Nonlinear Constraint Solver Algorithms for Genetic Algorithm.

Data Types: char | function_handle | string

`options` — Optimization options
output of `optimoptions` | structure

Optimization options, specified as the output of optimoptions or a structure.

optimoptions hides the options listed in italics. See Options that optimoptions Hides.

Values in {} denote the default value.
{}* represents the default when there are linear constraints, and for MutationFcn also when there are bounds.
I* indicates default for integer constraints, or indicates special considerations for integer constraints.
NM indicates that the option does not apply to gamultiobj.

Options for ga and gamultiobj

Option	Description	Values
`ConstraintTolerance`	Determines the feasibility with respect to nonlinear constraints. Also, `max(sqrt(eps),ConstraintTolerance)` determines feasibility with respect to linear constraints. For an options structure, use `TolCon`.	Nonnegative scalar \| `{1e-3}`
`CreationFcn`	Function that creates the initial population. Specify as a name of a built-in creation function or a function handle. See Population Options.	`{'gacreationuniform'}` \| `{'gacreationlinearfeasible'}` \| `'gacreationnonlinearfeasible'` \| `{'gacreationuniformint'}`I for `ga` \| `{'gacreationsobol'}`I* for `gamultiobj` \| Custom creation function
`CrossoverFcn`	Function that the algorithm uses to create crossover children. Specify as a name of a built-in crossover function or a function handle. See Crossover Options.	`{'crossoverscattered'}` for `ga`, `{'crossoverintermediate'}` for `gamultiobj` \| `{'crossoverlaplace'}`I \| `'crossoverheuristic'` \| `'crossoversinglepoint'` \| `'crossovertwopoint'` \| `'crossoverarithmetic'` \| Custom crossover function
`CrossoverFraction`	The fraction of the population at the next generation, not including elite children, that the crossover function creates.	Nonnegative scalar \| `{0.8}`
`Display`	Level of display.	`'off'` \| `'iter'` \| `'diagnose'` \| `{'final'}`
`DistanceMeasureFcn`	Function that computes the distance measure of individuals. Specify as a name of a built-in distance measure function or a function handle. The value applies to the decision variable or design space (genotype) or to function space (phenotype). The default `'distancecrowding'` is in function space (phenotype). For `gamultiobj` only. See Multiobjective Options. For an options structure, use a function handle, not a name.	`{'distancecrowding'}` means the same as `{@distancecrowding,'phenotype'}` \| `{@distancecrowding,'genotype'}` \| Custom distance function
`EliteCount`	NM Positive integer specifying how many individuals in the current generation are guaranteed to survive to the next generation. Not used in `gamultiobj`.	Nonnegative integer \| `{ceil(0.05PopulationSize)}` \| `{0.05(default PopulationSize)}` for mixed-integer problems
`FitnessLimit`	NM If the fitness function attains the value of `FitnessLimit`, the algorithm halts.	Scalar \| `{-Inf}`
`FitnessScalingFcn`	Function that scales the values of the fitness function. Specify as a name of a built-in scaling function or a function handle. Option unavailable for `gamultiobj`.	`{'fitscalingrank'}` \| `'fitscalingshiftlinear'` \| `'fitscalingprop'` \| `'fitscalingtop'` \| Custom fitness scaling function
`FunctionTolerance`	The algorithm stops if the average relative change in the best fitness function value over `MaxStallGenerations` generations is less than or equal to `FunctionTolerance`. If `StallTest` is `'geometricWeighted'`, then the algorithm stops if the weighted average relative change is less than or equal to `FunctionTolerance`. For `gamultiobj`, the algorithm stops when the geometric average of the relative change in value of the spread over `options.MaxStallGenerations` generations is less than `options.FunctionTolerance`, and the final spread is less than the mean spread over the past `options.MaxStallGenerations` generations. See gamultiobj Algorithm. For an options structure, use `TolFun`.	Nonnegative scalar \| `{1e-6}` for `ga`, `{1e-4}` for `gamultiobj`
`HybridFcn`	I* Function that continues the optimization after `ga` terminates. Specify as a name or a function handle. Alternatively, a cell array specifying the hybrid function and its options. See ga Hybrid Function. For `gamultiobj`, the only hybrid function is `@fgoalattain`. See gamultiobj Hybrid Function. When the problem has integer constraints, you cannot use a hybrid function. See When to Use a Hybrid Function.	Function name or handle \| `'fminsearch' \| 'patternsearch' \| 'fminunc' \| 'fmincon' \| {[]}` or 1-by-2 cell array \| `{@solver, hybridoptions}`, where `solver = fminsearch`, `patternsearch`, `fminunc`, or `fmincon` `{[]}`
InitialPenalty	NM I* Initial value of the penalty parameter	Positive scalar \| `{10}`
`InitialPopulationMatrix`	Initial population used to seed the genetic algorithm. Has up to `PopulationSize` rows and `N` columns, where `N` is the number of variables. You can pass a partial population, meaning one with fewer than `PopulationSize` rows. In that case, the genetic algorithm uses `CreationFcn` to generate the remaining population members. See Population Options. For an options structure, use `InitialPopulation`.	Matrix \| `{[]}`
`InitialPopulationRange`	Matrix or vector specifying the range of the individuals in the initial population. Applies to `gacreationuniform` creation function. `ga` shifts and scales the default initial range to match any finite bounds. For an options structure, use `PopInitRange`.	Matrix or vector \| `{[-10;10]}` for unbounded components, `{[-1e4+1;1e4+1]}` for unbounded components of integer-constrained problems, `{[lb;ub]}` for bounded components, with the default range modified to match one-sided bounds
`InitialScoresMatrix`	Initial scores used to determine fitness. Has up to `PopulationSize` rows and `Nf` columns, where `Nf` is the number of fitness functions (`1` for `ga`, greater than `1` for `gamultiobj`). You can pass a partial scores matrix, meaning one with fewer than `PopulationSize` rows. In that case, the solver fills in the scores when it evaluates the fitness functions. For an options structure, use `InitialScores`.	Column vector for single objective \| matrix for multiobjective \| `{[]}`
`MaxGenerations`	Maximum number of iterations before the algorithm halts. For an options structure, use `Generations`.	Nonnegative integer \|`{100numberOfVariables}` for `ga`, `{200numberOfVariables}` for `gamultiobj`
`MaxStallGenerations`	The algorithm stops if the average relative change in the best fitness function value over `MaxStallGenerations` generations is less than or equal to `FunctionTolerance`. If `StallTest` is `'geometricWeighted'`, then the algorithm stops if the weighted average relative change is less than or equal to `FunctionTolerance`. For `gamultiobj`, the algorithm stops when the geometric average of the relative change in value of the spread over `options.MaxStallGenerations` generations is less than `options.FunctionTolerance`, and the final spread is less than the mean spread over the past `options.MaxStallGenerations` generations. See gamultiobj Algorithm. For an options structure, use `StallGenLimit`.	Nonnegative integer \| `{50}` for `ga`, `{100}` for `gamultiobj`
`MaxStallTime`	NM The algorithm stops if there is no improvement in the objective function for `MaxStallTime` seconds, as measured by `tic` and `toc`. For an options structure, use `StallTimeLimit`.	Positive scalar `\| {Inf}`
`MaxTime`	The algorithm stops after running for `MaxTime` seconds, as measured by `tic` and `toc`. This limit is enforced after each iteration, so `ga` can exceed the limit when an iteration takes substantial time. For an options structure, use `TimeLimit`.	Nonnegative scalar \| `{Inf}`
MigrationDirection	Direction of migration. See Migration Options.	`'both'` \| `{'forward'}`
MigrationFraction	Scalar from 0 through 1 specifying the fraction of individuals in each subpopulation that migrates to a different subpopulation. See Migration Options.	Scalar \| `{0.2}`
MigrationInterval	Positive integer specifying the number of generations that take place between migrations of individuals between subpopulations. See Migration Options.	Positive integer \| `{20}`
`MutationFcn`	Function that produces mutation children. Specify as a name of a built-in mutation function or a function handle. See Mutation Options.	`{'mutationgaussian'}` for `ga` without constraints \| `{'mutationadaptfeasible'}` for `gamultiobj` and for `ga` with constraints \| `{'mutationpower'}`I \| `'mutationpositivebasis'` \| `'mutationuniform'` \| Custom mutation function
`NonlinearConstraintAlgorithm`	Nonlinear constraint algorithm. See Nonlinear Constraint Solver Algorithms for Genetic Algorithm. Option unchangeable for `gamultiobj`. For an options structure, use `NonlinConAlgorithm`.	`{'auglag'}` for `ga`, `{'penalty'}` for `gamultiobj`
`OutputFcn`	Functions that `ga` calls at each iteration. Specify as a function handle or a cell array of function handles. See Output Function Options. For an options structure, use `OutputFcns`.	Function handle or cell array of function handles \| `{[]}`
`ParetoFraction`	Scalar from 0 through 1 specifying the fraction of individuals to keep on the first Pareto front while the solver selects individuals from higher fronts, for `gamultiobj` only. See Multiobjective Options.	Scalar \| `{0.35}`
PenaltyFactor	NM I* Penalty update parameter.	Positive scalar \| `{100}`
`PlotFcn`	Function that plots data computed by the algorithm. Specify as a name of a built-in plot function, a function handle, or a cell array of built-in names or function handles. See Plot Options. For an options structure, use `PlotFcns`.	`ga` or `gamultiobj`: `{[]} \| 'gaplotdistance' \| 'gaplotgenealogy' \| 'gaplotselection' \| 'gaplotscorediversity' \|'gaplotscores' \| 'gaplotstopping' \| 'gaplotmaxconstr' \|`Custom plot function `ga` only: `'gaplotbestf' \| 'gaplotbestindiv' \| 'gaplotexpectation' \| 'gaplotrange'` `gamultiobj` only: `'gaplotpareto' \| 'gaplotparetodistance' \| 'gaplotrankhist' \| 'gaplotspread'`
PlotInterval	Positive integer specifying the number of generations between consecutive calls to the plot functions.	Positive integer \| `{1}`
`PopulationSize`	Size of the population.	Positive integer \| `{50}` when `numberOfVariables <= 5`, `{200}` otherwise \| `{min(max(10*nvars,40),100)}` for mixed-integer problems
`PopulationType`	Data type of the population. Must be `'doubleVector'` for mixed-integer problems.	`'bitstring'` \| `'custom'` \| `{'doubleVector'}` `ga` ignores all constraints when `PopulationType` is set to `'bitString'` or `'custom'`. See Population Options.
`SelectionFcn`	Function that selects parents of crossover and mutation children. Specify as a name of a built-in selection function or a function handle. `gamultiobj` uses only `'selectiontournament'`.	`{'selectionstochunif'}` for `ga`, `{'selectiontournament'}` for `gamultiobj` \| `'selectionremainder'` \| `'selectionuniform'` \| `'selectionroulette'` \| Custom selection function
StallTest	NM Stopping test type.	`'geometricWeighted'` \| `{'averageChange'}`
`UseParallel`	Compute fitness and nonlinear constraint functions in parallel. See Vectorize and Parallel Options (User Function Evaluation) and How to Use Parallel Processing in Global Optimization Toolbox.	`true` \| `{false}`
`UseVectorized`	Specifies whether functions are vectorized. See Vectorize and Parallel Options (User Function Evaluation) and Vectorize the Fitness Function. For an options structure, use `Vectorized` with the values `'on'` or `'off'`.	`true` \| `{false}`

Example: optimoptions('ga','PlotFcn',@gaplotbestf)

`intcon` — Integer variables
vector of positive integers

Integer variables, specified as a vector of positive integers taking values from 1 to nvars. Each value in intcon represents an x component that is integer-valued.

Note

When intcon is nonempty, nonlcon must return empty for ceq. For more information on integer programming, see Mixed Integer ga Optimization.

Example: To specify that the even entries in x are integer-valued, set intcon to 2:2:nvars

Data Types: double

`problem` — Problem description
structure

Problem description, specified as a structure containing these fields.

`fitnessfcn`	Fitness functions
`nvars`	Number of design variables
`Aineq`	`A` matrix for linear inequality constraints
`Bineq`	`b` vector for linear inequality constraints
`Aeq`	`Aeq` matrix for linear equality constraints
`Beq`	`beq` vector for linear equality constraints
`lb`	Lower bound on `x`
`ub`	Upper bound on `x`
`nonlcon`	Nonlinear constraint functions
`intcon`	Indices of integer variables
`rngstate`	Field to reset the state of the random number generator
`solver`	`'ga'`
`options`	Options created using `optimoptions` or an options structure

You must specify the fields fitnessfcn, nvars, and options. The remainder are optional for ga.

Data Types: struct

Output Arguments

collapse all

`x` — Solution
real vector

Solution, returned as a real vector. x is the best point that ga located during its iterations.

`fval` — Objective function value at the solution
real number

Objective function value at the solution, returned as a real number. Generally, fval = fun(x).

`exitflag` — Reason `ga` stopped
integer

Reason that ga stopped, returned as an integer.

Exit Flag	Meaning
`1`	Without nonlinear constraints — Average cumulative change in value of the fitness function over `MaxStallGenerations` generations is less than `FunctionTolerance`, and the constraint violation is less than `ConstraintTolerance`.
`1`	With nonlinear constraints — Magnitude of the complementarity measure (see Complementarity Measure) is less than `sqrt(ConstraintTolerance)`, the subproblem is solved using a tolerance less than `FunctionTolerance`, and the constraint violation is less than `ConstraintTolerance`.
`3`	Value of the fitness function did not change in `MaxStallGenerations` generations and the constraint violation is less than `ConstraintTolerance`.
`4`	Magnitude of step smaller than machine precision and the constraint violation is less than `ConstraintTolerance`.
`5`	Minimum fitness limit `FitnessLimit` reached and the constraint violation is less than `ConstraintTolerance`.
`0`	Maximum number of generations `MaxGenerations` exceeded.
`-1`	Optimization terminated by an output function or plot function.
`-2`	No feasible point found.
`-4`	Stall time limit `MaxStallTime` exceeded.
`-5`	Time limit `MaxTime` exceeded.

When there are integer constraints, ga uses the penalty fitness value instead of the fitness value for stopping criteria.

`output` — Information about the optimization process
structure

Information about the optimization process, returned as a structure with these fields:

problemtype — Problem type, one of:
- 'unconstrained'
- 'boundconstraints'
- 'linearconstraints'
- 'nonlinearconstr'
- 'integerconstraints'
rngstate — State of the MATLAB random number generator, just before the algorithm started. You can use the values in rngstate to reproduce the output of ga. See Reproduce Results.
generations — Number of generations computed.
funccount — Number of evaluations of the fitness function.
message — Reason the algorithm terminated.
maxconstraint — Maximum constraint violation, if any.
hybridflag — Exit flag from the hybrid function. Relates to the HybridFcn options. Not applicable to gamultiobj.

`population` — Final population
matrix

Final population, returned as a PopulationSize-by-nvars matrix. The rows of population are the individuals.

`scores` — Final scores
column vector

Final scores, returned as a column vector.

For non-integer problems, the final scores are the fitness function values of the rows of population.
For integer problems, the final scores are the penalty fitness values of the population members. See Integer ga Algorithm.

More About

collapse all

Complementarity Measure

In the Augmented Lagrangian nonlinear constraint solver, the complementarity measure is the norm of the vector whose elements are c_iλ_i, where c_i is the nonlinear inequality constraint violation, and λ_i is the corresponding Lagrange multiplier. See Augmented Lagrangian Genetic Algorithm.

Tips

To write a function with additional parameters to the independent variables that can be called by ga, see Passing Extra Parameters.
For problems that use the population type Double Vector (the default), ga does not accept functions whose inputs are of type complex. To solve problems involving complex data, write your functions so that they accept real vectors, by separating the real and imaginary parts.

Algorithms

For a description of the genetic algorithm, see How the Genetic Algorithm Works.

For a description of the mixed integer programming algorithm, see Integer ga Algorithm.

For a description of the nonlinear constraint algorithms, see Nonlinear Constraint Solver Algorithms for Genetic Algorithm.

Alternative Functionality

App

The Optimize Live Editor task provides a visual interface for ga.

References

[1] Goldberg, David E., Genetic Algorithms in Search, Optimization & Machine Learning, Addison-Wesley, 1989.

[2] A. R. Conn, N. I. M. Gould, and Ph. L. Toint. “A Globally Convergent Augmented Lagrangian Algorithm for Optimization with General Constraints and Simple Bounds”, SIAM Journal on Numerical Analysis, Volume 28, Number 2, pages 545–572, 1991.

[3] A. R. Conn, N. I. M. Gould, and Ph. L. Toint. “A Globally Convergent Augmented Lagrangian Barrier Algorithm for Optimization with General Inequality Constraints and Simple Bounds”, Mathematics of Computation, Volume 66, Number 217, pages 261–288, 1997.

Extended Capabilities

Automatic Parallel Support
Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.

To run in parallel, set the 'UseParallel' option to true.

options = optimoptions('solvername','UseParallel',true)

For more information, see How to Use Parallel Processing in Global Optimization Toolbox.

Version History

Introduced before R2006a

expand all

R2019b: `ga` Performs Fewer Fitness Function Evaluations

When the fitness function is deterministic, ga does not reevaluate the fitness function on elite (current best) individuals. You can control this behavior by accessing the new state.EvalElites field and modifying it in a custom output function or custom plot function. Similarly, when the initial population has duplicate members, ga evaluates each unique member only once. You can control this behavior in a custom output function or custom plot function by accessing and modifying the new state.HaveDuplicates field. For details, see Custom Output Function for Genetic Algorithm or Custom Plot Function.

For details about the two new fields, see The State Structure.

ga

Syntax

Description

Examples

Optimize a Nonsmooth Function Using ga

Minimize a Nonsmooth Function with Linear Constraints

Minimize a Nonsmooth Function with Linear Equality and Inequality Constraints

Optimize with Linear Constraints and Bounds

Optimize with Nonlinear Constraints Using ga

Minimize with Nondefault Options

Minimize a Nonlinear Function with Integer Constraints

Obtain the Solution and Function Value

Obtain Diagnostic Information

Obtain Final Population and Scores

Input Arguments

fun — Objective function function handle | function name

nvars — Number of variables positive integer

A — Linear inequality constraints real matrix

b — Linear inequality constraints real vector

Aeq — Linear equality constraints real matrix

beq — Linear equality constraints real vector

lb — Lower bounds [] (default) | real vector or array

ub — Upper bounds [] (default) | real vector or array

nonlcon — Nonlinear constraints function handle | function name

options — Optimization options output of optimoptions | structure

intcon — Integer variables vector of positive integers

problem — Problem description structure

Output Arguments

x — Solution real vector

fval — Objective function value at the solution real number

exitflag — Reason ga stopped integer

output — Information about the optimization process structure

population — Final population matrix

scores — Final scores column vector

More About

Complementarity Measure

Tips

Algorithms

Alternative Functionality

App

References

Extended Capabilities

Automatic Parallel Support Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.

Version History

R2019b: ga Performs Fewer Fitness Function Evaluations

See Also

Topics

Optimize a Nonsmooth Function Using `ga`

Optimize with Nonlinear Constraints Using `ga`

`fun` — Objective function
function handle | function name

`nvars` — Number of variables
positive integer

`A` — Linear inequality constraints
real matrix

`b` — Linear inequality constraints
real vector

`Aeq` — Linear equality constraints
real matrix

`beq` — Linear equality constraints
real vector

`lb` — Lower bounds
`[]` (default) | real vector or array

`ub` — Upper bounds
`[]` (default) | real vector or array

`nonlcon` — Nonlinear constraints
function handle | function name

`options` — Optimization options
output of `optimoptions` | structure

`intcon` — Integer variables
vector of positive integers

`problem` — Problem description
structure

`x` — Solution
real vector

`fval` — Objective function value at the solution
real number

`exitflag` — Reason `ga` stopped
integer

`output` — Information about the optimization process
structure

`population` — Final population
matrix

`scores` — Final scores
column vector

Automatic Parallel Support
Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.

R2019b: `ga` Performs Fewer Fitness Function Evaluations