遗传算法的工作原理
算法概述
以下概述了遗传算法的工作原理:
该算法首先创建一个随机初始种群。
然后,该算法会创建一系列新的种群。在每一步中,算法使用当前代中的个体来创建下一代种群。为了创建新的种群,算法执行以下步骤:
通过计算适应度值对当前种群的每个成员进行评分。这些值被称为原始适应度分数。
缩放原始适应度分数以将其转换为更可用的值范围。这些缩放值被称为期望值。
根据期望选择成员,称为父代。
当前种群中一些适应度较低的个体被选为精英。这些精英个体被传递给下一个种群。
父代产生子代。子代的产生要么通过对单个父代进行随机改变 -变异- 要么通过组合一对父代的向量条目 -交叉。
用子代取代当前的种群来形成下一代。
当满足其中一个停止条件时,算法停止。请参阅 算法的停止条件。
该算法针对线性和整数约束采取了修改的步骤。请参阅 整数和线性约束。
该算法针对非线性约束进行了进一步的修改。请参阅 遗传算法算法的非线性约束求解算法。
初始种群
该算法首先创建一个随机初始种群,如下图所示。
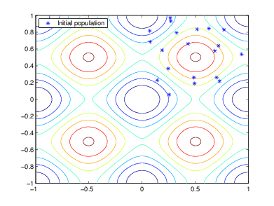
在这个例子中,初始种群包含 20 个体。注意初始种群中的所有个体都位于图片的右上象限,即它们的坐标位于 0 到 1 之间。对于此示例,InitialPopulationRange 选项是 [0;1]。
如果您大致知道函数的最小点位于何处,则应设置 InitialPopulationRange 以使该点位于该范围的中间附近。例如,如果您认为拉斯特里金函数的最小点在点 [0 0] 附近,那么您可以将 InitialPopulationRange 设置为 [-1;1]。然而,正如这个例子所示,即使 InitialPopulationRange 的选择不是最优的,遗传算法也可以找到最小值。
创建下一代
在每个步骤中,遗传算法都会使用当前种群来创建构成下一代的子代。该算法在当前种群中选择一组个体,称为父代,它们将自己的基因(即其向量的条目)贡献给它们的子代。该算法通常选择适应度值较好的个体作为父代。您可以在 SelectionFcn 选项中指定算法用于选择父代的函数。请参阅 选择选项。
遗传算法为代创建了三种类型的子代:
精英子代是当前代中适应最佳适应度的个体。这些个体会自动存活到下一代。
交叉子代是通过组合一对父代的向量而创建的。
突变子代是通过向单个父代引入随机改变或突变而创建的。
下面的示意图说明了这三种类型的子项。
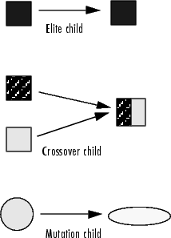
变异和交叉 解释了如何指定算法生成的每种类型的子项数量以及用于执行交叉和变异的函数。
以下部分解释了该算法如何创建交叉和变异子代。
交叉子代
该算法通过组合当前种群中的父代对来创建交叉子代。在子向量的每个坐标上,默认的交叉函数从两个父代之一的相同坐标处随机选择一个条目或基因,并将其分配给子代。对于具有线性约束的问题,默认的交叉函数子代创建父代的随机加权平均值。
突变子代
该算法通过随机更改单个父代的基因来创建变异子代。默认情况下,对于无约束问题,算法会将高斯分布的随机向量添加到父代。对于有界或线性约束的问题,子问题仍然是可行的。
下图显示了初始种群的子代,即第二代种群,并指出它们是精英、交叉子代还是变异子代。
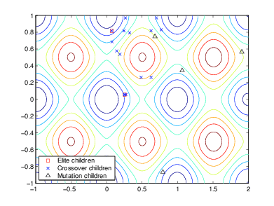
后代绘图
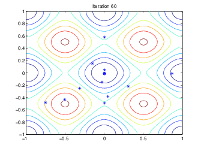
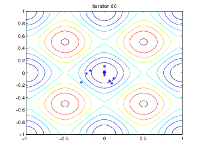
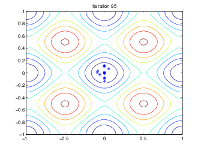
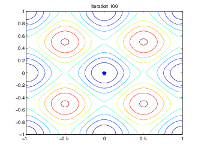
下图显示了第 60、80、95 和 100 次迭代的群体情况。
|
|
|
|
|
|
随着代数的增加,种群中个体之间的距离越来越近,趋向于最小值点 [0 0]。
算法的停止条件
遗传算法使用以下选项来确定何时停止。通过运行 opts = optimoptions('ga') 查看每个选项的默认值。
MaxGenerations- 当代数达到MaxGenerations时,算法停止。MaxTime- 算法运行等于MaxTime的秒数后停止。FitnessLimit- 当当前种群中最佳点的适应度函数值小于或等于FitnessLimit时,算法停止。MaxStallGenerations- 当MaxStallGenerations上的适应度函数值的平均相对变化小于Function tolerance时,算法停止。MaxStallTime- 如果在等于MaxStallTime的秒数时间间隔内目标函数没有任何改善,则算法停止。FunctionTolerance- 算法运行直到适应度函数值在MaxStallGenerations上的平均相对变化小于Function tolerance。ConstraintTolerance-ConstraintTolerance不用作停止条件。它用于确定非线性约束的可行性。另外,max(sqrt(eps),ConstraintTolerance)确定在线性约束下的可行性。
一旦满足其中任何一个条件,算法就会停止。
选择
选择函数根据适应度缩放函数的缩放值来选择下一代父母。缩放的适应度值称为期望值。一个个体可以被多次选为父代,在这种情况下,它会将其基因贡献给多个子代。默认选择选项 @selectionstochunif 布置一条线,其中每个父代对应一段长度与其缩放值成比例的线。该算法以相同大小的步长沿着线移动。在每个步骤中,算法都会从其所在的部分分配一个父代。
更确定的选择选项是 @selectionremainder,它执行两个步骤:
第一步,该函数根据每个个体的缩放值的整数部分确定性地选择父代。例如,如果某个个体的缩放值为 2.3,则该函数会两次选择该个体作为父代。
在第二步中,选择函数使用缩放值的小数部分来选择其他父代,就像随机均匀选择一样。该函数分段布置一条线,其长度与个体缩放值的小数部分成比例,并以相等的步长沿着该线移动来选择父代。
请注意,如果缩放值的小数部分都等于 0(如使用
Top缩放出现的情况),则选择是完全确定的。
有关详细信息和更多选择选项,请参阅 选择选项。
重现选项
重现选项控制遗传算法如何创建代。选项包括
EliteCount当前一代中适应度值最佳且保证能存活到下一代的个体数量。这些个体被称为精英子代。当
EliteCount至少为 1 时,最佳适应度值只能从一代到下一代减少。这正是您想要发生的结果,因为遗传算法最小化了适应度函数。将EliteCount设置为较高的值会导致最适合的个体占据主导种群,从而降低搜索的效率。CrossoverFraction- 下一代中除精英子代以外,通过交叉产生的个体比例。变异和交叉 中的主题“设置交叉分数”描述了CrossoverFraction的值如何影响遗传算法的性能。
由于精英个体已经被评估,因此ga 不会在重现过程中重新评估精英个体的适应度函数。这种行为假设个体的适应度函数不是随机的,而是一个确定性函数。要改变此行为,请使用输出函数。请参阅 状态结构体 中的 EvalElites。
变异和交叉
遗传算法使用当前一代的个体来创建构成下一代的子代。除了精英子代(对应于当前代中适应最佳适应度的个体)之外,该算法还创建
通过从当前代中的一对个体中选择向量条目或基因来交叉子代,并将它们组合成一个子代
通过对当前代中的单个个体应用随机变化来创建子代,从而实现子代突变
这两个过程对于遗传算法来说都至关重要。交叉使算法能够从不同的个体中提取最佳基因,并将它们重新组合成潜在的优良后代。变异增加了种群的多样性,从而增加了算法产生具有更好适应度值的个体的可能性。
请参阅创建下一代 了解遗传算法如何应用变异和交叉的示例。
您可以指定算法创建的每种类型的子代的数量,如下所示:
EliteCount指定精英子代的数量。CrossoverFraction指定除精英子代之外的交叉子代占种群的比例。
例如,如果 PopulationSize 为 20,EliteCount 为 2,CrossoverFraction 为 0.8,则下一代中每种类型子代的数量如下:
有两个精英子代。
除了精英子代之外还有 18 个个体,因此算法将 0.8*18 = 14.4 四舍五入为 14 以获得交叉子代的数量。
其余四个体,除了精英子代外,都是变异子代。
整数和线性约束
当问题具有整数或线性约束(包括边界)时,算法会修改种群的进化。
当问题同时具有整数和线性约束时,软件会修改所有生成的个体,使其根据这些约束变得可行。您可以使用任何创建、变异或交叉函数,并且整个种群在整数和线性约束方面仍然可行。
当问题仅有线性约束时,软件不会修改个体以使其符合这些约束的可行。您必须使用创建、变异和交叉函数来保持相对于线性约束的可行性。否则,种群将变得不可行,结果也将不可行。默认运算符保持线性可行性:
gacreationlinearfeasible或gacreationnonlinearfeasible用于创建,mutationadaptfeasible用于变异,crossoverintermediate用于交叉。
整数和线性可行性的内部算法与 surrogateopt 的内部算法类似。当问题具有整数和线性约束时,算法首先创建线性可行点。然后,该算法尝试通过使用启发式方法将线性可行点四舍五入为整数来满足整数约束,该启发式方法试图保持点的线性可行。当此过程无法获取足够的可行点来构建种群时,算法将调用 intlinprog 来尝试查找更多符合边界、线性约束和整数约束的可行点。
之后,当变异或交叉产生新的种群成员时,算法通过采取类似的步骤确保新成员是整数且线性可行的。如果有必要,每个新成员都会被修改,以尽可能接近其原始值,同时满足整数和线性约束和边界。