多目标遗传算法选项的影响
这个例子展示了多目标遗传算法选项的一些效果。您可以使用 gamultiobj 函数创建和更改 optimoptions 的选项。
为 gamultiobj 设置问题
gamultiobj 使用遗传算法为多个目标函数找到局部帕累托前沿。对于此示例,使用 gamultiobj 获取 MATLAB® 文件 kur_multiobjective.m 中描述的两个目标函数的帕累托前沿。该文件表示一个实值函数,由两个目标组成,每个目标有三个决策变量。还对决策变量施加边界约束 -5 <= x(i) <= 5, i = 1,2,3。
type kur_multiobjective.mfunction y = kur_multiobjective(x) %KUR_MULTIOBJECTIVE Objective function for a multiobjective problem. % The Pareto-optimal set for this two-objective problem is nonconvex as % well as disconnected. The function KUR_MULTIOBJECTIVE computes two % objectives and returns a vector y of size 2-by-1. % % Reference: Kalyanmoy Deb, "Multi-Objective Optimization using % Evolutionary Algorithms", John Wiley & Sons ISBN 047187339 % Copyright 2007 The MathWorks, Inc. % Initialize for two objectives y = zeros(2,1); % Compute first objective for i = 1:2 y(1) = y(1) - 10*exp(-0.2*sqrt(x(i)^2 + x(i+1)^2)); end % Compute second objective for i = 1:3 y(2) = y(2) + abs(x(i))^0.8 + 5*sin(x(i)^3); end
为了观察求解器的进度,使用绘图函数 @gaplotpareto 绘制每代的帕累托前沿。使用 optimoptions 函数在选项中指定此绘图函数。
FitnessFunction = @kur_multiobjective; % Function handle to the fitness function numberOfVariables = 3; % Number of decision variables lb = [-5 -5 -5]; % Lower bound ub = [5 5 5]; % Upper bound A = []; % No linear inequality constraints b = []; % No linear inequality constraints Aeq = []; % No linear equality constraints beq = []; % No linear equality constraints options = optimoptions(@gamultiobj,'PlotFcn',@gaplotpareto);
运行 gamultiobj 求解器并显示在帕累托前沿找到的解的数量和代数。
[x,Fval,exitFlag,Output] = gamultiobj(FitnessFunction,numberOfVariables,A, ...
b,Aeq,beq,lb,ub,options);gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.
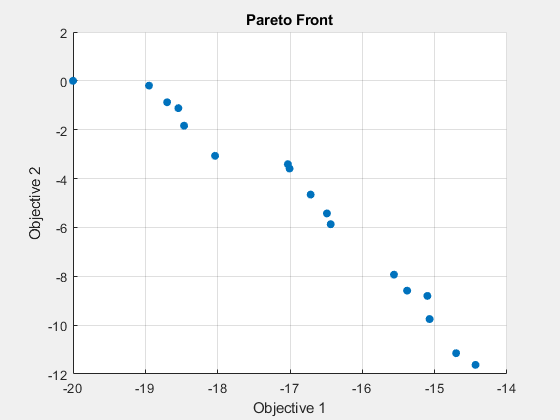
fprintf('The number of points on the Pareto front was: %d\n', size(x,1));The number of points on the Pareto front was: 18
fprintf('The number of generations was : %d\n', Output.generations);The number of generations was : 317
帕累托图显示了两个相互竞争的目标。对于这个问题,已知帕累托前沿是不连续的。来自 gamultiobj 的解即使断开连接也能捕获帕累托前沿。请注意,当您运行此示例时,您的结果可能与显示的结果不同,因为 gamultiobj 使用随机数生成器。
精英多目标遗传算法
多目标遗传算法(gamultiobj)使用一组适用于种群的运算符来对种群进行操作。种群是设计空间中的一组点。初始种群默认是随机生成的。使用非支配等级和当前一代个体的距离测量来计算下一代种群。
使用相对适应度为每个个体分配一个非支配排名。如果“p”在至少一个目标上严格优于“q”,并且“p”在所有目标中都不差于“q”,则目标“p”优于“q”(“p”的排名低于“q”)。这与说“q”受“p”支配或“p”不劣于“q”是一样的。如果两个个体 'p' 和 'q' 都不占优势,则认为它们具有相同的排名。个体的距离度量用于比较具有相同排名的个体。它衡量一个个体与具有相同排名的其他个体之间的距离。
多目标 GA 函数 gamultiobj 使用受控精英遗传算法(NSGA-II [1] 的变体)。精英遗传算法总是青睐具有更好适应度值(排名)的个体,而受控精英算法也会青睐那些可以帮助增加种群多样性的个体,即使它们具有较低的适应度值。保持种群的多样性对于收敛到最优帕累托前沿非常重要。这是通过随着算法的进展控制种群中的精英成员来实现的。两个选项“ParetoFraction”和“DistanceFcn”用于控制精英主义。帕累托分数选项限制了帕累托前沿(精英成员)上的个体数量,而距离函数通过偏爱前沿上相对较远的个体来帮助保持前沿的多样性。
指定多目标 GA 选项
我们可以选择工具箱中提供的默认距离测量函数 distancecrowding,或者编写我们自己的函数来计算个体的距离测量。工具箱中的拥挤距离测量函数采用可选参量来计算函数空间(表型)或设计空间(基因型)中的距离。如果选择 'genotype',那么帕累托前沿的多样性就基于设计空间。默认选择是 'phenotype',在这种情况下,多样性基于函数空间。这里我们选择 'genotype' 作为距离函数。我们将直接修改参数 DistanceMeasureFcn 的值。
options.DistanceMeasureFcn = {@distancecrowding,'genotype'};帕累托分数的默认值为 0.35,即,求解器将尝试将当前种群中位于帕累托前沿的个体数量限制为种群规模的 35%。这里我们将帕累托分数设置为 0.5。
options = optimoptions(options,'ParetoFraction',0.5);运行 gamultiobj 求解器并显示在帕累托前沿找到的解的数量和解的平均距离测量。
[x,Fval,exitFlag,Output] = gamultiobj(FitnessFunction,numberOfVariables,A, ...
b,Aeq,beq,lb,ub,options);gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.

fprintf('The number of points on the Pareto front was: %d\n', size(x,1));The number of points on the Pareto front was: 25
fprintf('The average distance measure of the solutions on the Pareto front was: %g\n', Output.averagedistance);The average distance measure of the solutions on the Pareto front was: 0.051005
fprintf('The spread measure of the Pareto front was: %g\n', Output.spread);The spread measure of the Pareto front was: 0.181192
较小的平均距离测量表明帕累托前沿上的解分布均匀。然而,如果帕累托前沿断开,那么距离测量将无法指示解的真实分布。
修改停止标准
gamultiobj 使用三个不同的标准来确定何时停止求解器。当满足任何一个停止条件时,求解器就会停止。当达到最大代数时,它会停止;默认情况下,这个数字是 '200*numberOfVariables'。如果 gamultiobj 代(默认值为 100)中帕累托前沿的扩展平均变化小于 MaxStallGenerations 中指定的容差,options.FunctionTolerance 也会停止。第三个标准是最大时间限制(以秒为单位)(默认为 Inf)。这里我们修改了停止条件,将 FunctionTolerance 从 1e-4 更改为 1e-3,并将 MaxStallGenerations 增加到 150。
options = optimoptions(options,'FunctionTolerance',1e-3,'MaxStallGenerations',150);
运行 gamultiobj 求解器并显示在帕累托前沿找到的解的数量和代数。
[x,Fval,exitFlag,Output] = gamultiobj(FitnessFunction,numberOfVariables,A, ...
b,Aeq,beq,lb,ub,options);gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.
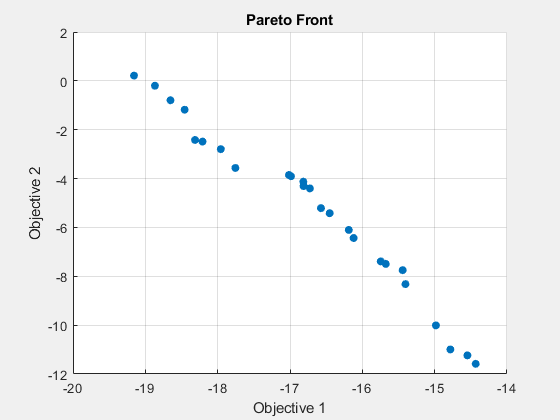
fprintf('The number of points on the Pareto front was: %d\n', size(x,1));The number of points on the Pareto front was: 25
fprintf('The number of generations was : %d\n', Output.generations);The number of generations was : 152
多目标遗传算法混合函数
我们将使用混合方案为我们的多目标问题寻找最优帕累托前沿。gamultiobj 可以相对较快地到达最优帕累托前沿附近的区域,但可能需要多次函数计算才能实现收敛。一种常用的技术是运行 gamultiobj 少数几代以接近最佳前沿。然后,将 gamultiobj 的解用作另一个优化求解器的初始点,该求解器对于局部搜索来说更快、更高效。我们使用 fgoalattain 作为与 gamultiobj 的混合求解器。fgoalattain 解决目标实现问题,这是最小化多目标优化问题的一种公式。
多目标函数 gamultiobj 中的混合函数与单目标函数 GA 略有不同。在单目标 GA 中,混合函数从 GA 返回的最佳点开始。然而,在 gamultiobj 中,混合求解器将从 gamultiobj 返回的帕累托前沿上的所有点开始。混合求解器返回的新个体与现有种群相结合,得到新的帕累托前沿。查看 fgoalattain 函数的语法可能对更好地理解 gamultiobj 的输出如何在内部转换为 fgoalattain 函数的输入有帮助。gamultiobj 估计帕累托前沿上每个点的伪权重(fgoalattain 所需的输入)并从帕累托前沿上的每个点开始运行混合求解器。另一个必需的输入,目标,是一个指定每个目标的目标的向量。gamultiobj 将此输入作为迄今为止找到的帕累托前沿的极值点。
这里我们运行不使用混合函数的 gamultiobj。
[x,Fval,exitFlag,Output] = gamultiobj(FitnessFunction,numberOfVariables,A, ...
b,Aeq,beq,lb,ub,options);gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.
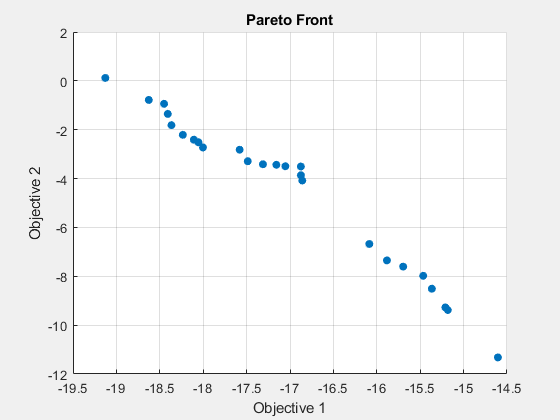
fprintf('The number of points on the Pareto front was: %d\n', size(x,1));The number of points on the Pareto front was: 25
fprintf('The average distance measure of the solutions on the Pareto front was: %g\n', Output.averagedistance);The average distance measure of the solutions on the Pareto front was: 0.0434477
fprintf('The spread measure of the Pareto front was: %g\n', Output.spread);The spread measure of the Pareto front was: 0.17833
这里我们使用 fgoalattain 作为混合函数。我们还重置了随机数生成器,以便我们可以将结果与上次运行(没有混合函数)进行比较。
options = optimoptions(options,'HybridFcn',@fgoalattain);重置随机状态(仅与上次运行进行比较)
strm = RandStream.getGlobalStream; strm.State = Output.rngstate.State;
运行具有混合函数的 GAMULTIOBJ 求解器。
[x,Fval,exitFlag,Output,Population,Score] = gamultiobj(FitnessFunction,numberOfVariables,A, ...
b,Aeq,beq,lb,ub,options);gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.
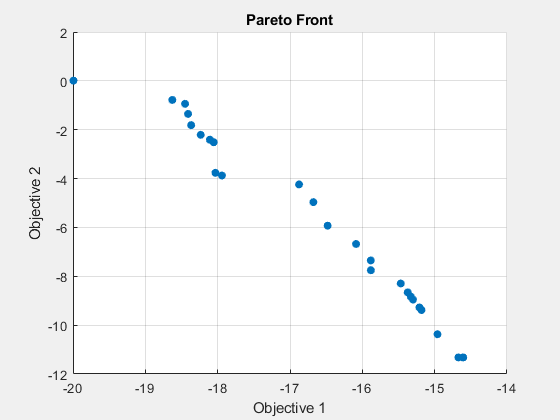
fprintf('The number of points on the Pareto front was: %d\n', size(x,1));The number of points on the Pareto front was: 25
fprintf('The average distance measure of the solutions on the Pareto front was: %g\n', Output.averagedistance);The average distance measure of the solutions on the Pareto front was: 0.127898
fprintf('The spread measure of the Pareto front was: %g\n', Output.spread);The spread measure of the Pareto front was: 0.420549
如果单独通过 gamultiobj 和使用混合函数获得的帕累托前沿接近,我们可以使用扩展和平均距离测量对它们进行比较。可以使用混合函数来改善帕累托前沿上的解的平均距离。价差是两个前沿变化的量度,当使用混合函数时,价差可能会更高。这表明锋面与没有混合函数的 gamultiobj 获得的锋面相比发生了很大变化。
可以肯定的是,使用混合函数将产生最优的帕累托前沿,但我们可能会失去解的多样性(因为 fgoalattain 不会尝试保持多样性)。这可以通过平均距离测量值的较高和前沿的扩展来表明。我们可以通过再次运行 gamultiobj 并使用上次运行中返回的最终种群来进一步改进解的平均距离测量和帕累托前沿的扩展。这里,我们应该删除混合函数。
options = optimoptions(options,'HybridFcn',[]); % No hybrid function % Provide initial population and scores options = optimoptions(options,'InitialPopulationMatrix',Population,'InitialScoresMatrix',Score); % Run the GAMULTIOBJ solver with hybrid function. [x,Fval,exitFlag,Output,Population,Score] = gamultiobj(FitnessFunction,numberOfVariables,A, ... b,Aeq,beq,lb,ub,options);
gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.
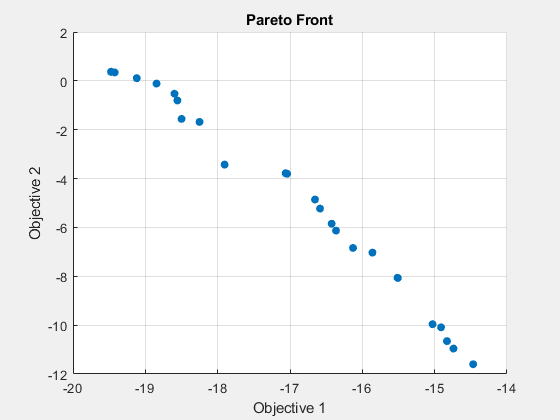
fprintf('The number of points on the Pareto front was: %d\n', size(x,1));The number of points on the Pareto front was: 25
fprintf('The average distance measure of the solutions on the Pareto front was: %g\n', Output.averagedistance);The average distance measure of the solutions on the Pareto front was: 0.0527341
fprintf('The spread measure of the Pareto front was: %g\n', Output.spread);The spread measure of the Pareto front was: 0.20726
参考资料
[1] Kalyanmoy Deb, "Multi-Objective Optimization using Evolutionary Algorithms", John Wiley & Sons ISBN 047187339.