遗传算法中的混合方案
此示例说明如何使用混合方案,使用遗传算法和另一种优化方法来优化函数。ga 可以快速到达局部最小值的邻域,但它可能需要许多函数计算才能实现收敛。为了加快解决过程,首先运行少数几代 ga 来接近最佳点。然后使用来自 ga 的解作为另一个优化求解器的起点,执行更快、更有效的局部搜索。
罗森布罗克函数
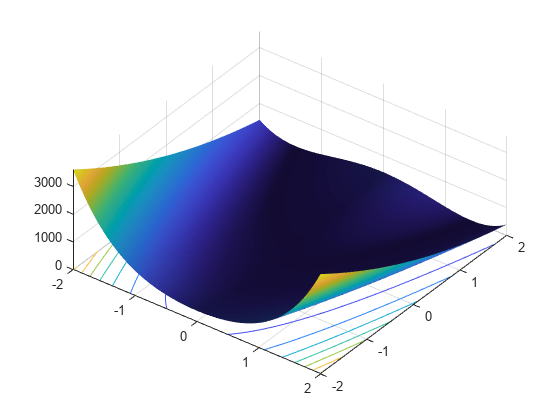
本例采用罗森布洛克函数(又称 Dejong 第二函数)作为适应度函数:
.
罗森布洛克函数在优化领域臭名昭著,因为大多数方法在尝试最小化该函数时都会表现出缓慢的收敛速度。罗森布洛克函数在点 x* = (1,1) 处具有唯一的最小值,该处它的函数值是 。
罗森布洛克函数的代码位于 dejong2fcn 文件中。
type dejong2fcn.mfunction scores = dejong2fcn(pop)
%DEJONG2FCN Compute DeJongs second function.
%This function is also known as Rosenbrock's function
% Copyright 2003-2004 The MathWorks, Inc.
scores = zeros(size(pop,1),1);
for i = 1:size(pop,1)
p = pop(i,:);
scores(i) = 100 * (p(1)^2 - p(2)) ^2 + (1 - p(1))^2;
end
在范围 –2 <= x(1) <= 2; –2 <= x(2) <=2 内绘制罗森布洛克函数。
plotobjective(@dejong2fcn,[-2 2;-2 2]);
遗传算法解
首先,单独使用 ga 来找到罗森布洛克函数的最小值。
FitnessFcn = @dejong2fcn; numberOfVariables = 2;
包括绘图函数来监控优化过程。
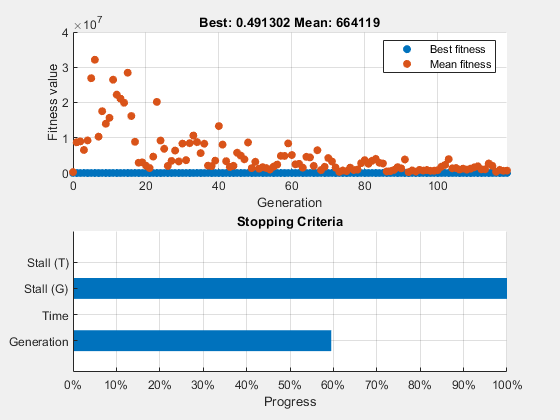
options = optimoptions(@ga,'PlotFcn',{@gaplotbestf,@gaplotstopping});设置随机数流以实现可再现性,并使用选项运行 ga。
rng default
[x,fval] = ga(FitnessFcn,numberOfVariables,[],[],[],[],[],[],[],options)ga stopped because the average change in the fitness value is less than options.FunctionTolerance.
x = 1×2
0.3454 0.1444
fval = 0.4913
使用默认的停止条件,ga 不能提供非常精确的解。您可以更改停止条件来尝试找到更准确的解,但 ga 需要多次函数计算才能接近全局最优 x* = (1,1)。
相反,使用 ga 中的混合函数选项,从 ga 停止的地方开始执行更有效的局部搜索。
添加混合函数
混合函数从 ga 停止的地方开始。混合函数选择是 fminsearch、patternsearch 或 fminunc。由于该优化示例平滑且无约束,因此使用 fminunc 作为混合函数。在指定混合函数时,提供 fminunc 和绘图选项作为附加参量。
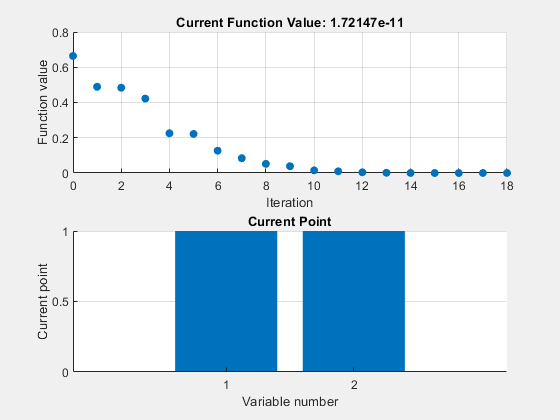
fminuncOptions = optimoptions(@fminunc,'PlotFcn',{'optimplotfval','optimplotx'}); options = optimoptions(options,'HybridFcn',{@fminunc, fminuncOptions});
再次运行 ga,并以 fminunc 作为混合函数。
[x,fval,exitflag,output] = ga(FitnessFcn,numberOfVariables,[],[],[],[],[],[],[],options)
ga stopped because the average change in the fitness value is less than options.FunctionTolerance.
Local minimum found. Optimization completed because the size of the gradient is less than the value of the optimality tolerance. <stopping criteria details>

x = 1×2
1.0000 1.0000
fval = 1.7215e-11
exitflag = 1
output = struct with fields:
problemtype: 'unconstrained'
rngstate: [1×1 struct]
generations: 51
funccount: 2534
message: 'ga stopped because the average change in the fitness value is less than options.FunctionTolerance.↵FMINUNC: Local minimum found.↵↵Optimization completed because the size of the gradient is less than↵the value of the optimality tolerance.↵↵<stopping criteria details>↵↵Optimization completed: The first-order optimality measure, 2.473362e-07, is less ↵than options.OptimalityTolerance = 1.000000e-06.↵'
maxconstraint: []
hybridflag: 1
ga 图显示了每代种群的最佳值和平均值。图表标题标识了 ga 停止时找到的最佳值。混合函数 fminunc 从 ga 找到的最佳点开始。fminunc 图显示了解 x 和 fval,它们是使用 ga 和 fminunc 一起使用的结果。在这种情况下,使用混合函数可以提高解的准确性和效率。output.hybridflag 字段显示 fminunc 以退出标志 1 停止,这表明 x 是一个真正的局部最小值。