本页采用了机器翻译。点击此处可查看最新英文版本。

使用 ga 进行全局优化与局部优化

打开实时脚本

寻找全局最小值

有时，优化的目标是找到函数的全局最小值或最大值-函数在搜索空间中的任何其他点都小于或大于该点。然而，优化算法有时会返回局部最小值-该点的函数值小于附近点，但可能大于搜索空间中远处点的函数值。遗传算法有时可以通过正确的设置来克服这一缺陷。

作为示例，考虑以下函数。

f(x)={-exp(-(x100)2)forx≤100,-exp(-1)+(x-100)(x-102)forx>100.

绘制函数。

t = -10:.1:103;
for ii = 1:length(t)
    y(ii) = two_min(t(ii));
end
plot(t,y)

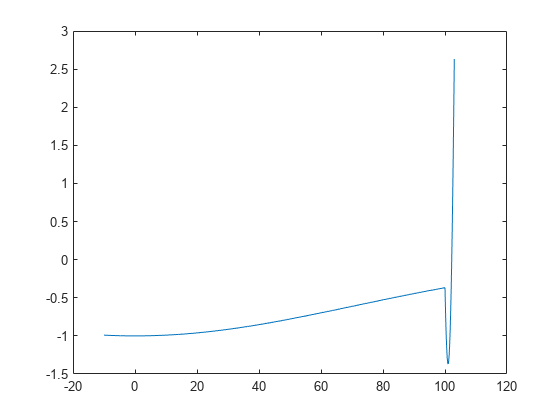
Figure contains an axes object. The axes object contains an object of type line.

该函数有两个局部极小值，一个在 x = 0，其中函数值为 -1，另一个在 x = 101，其中函数值为 –1 – 1/e。由于后者的值较小，全局最小值出现在 x = 101 处。

使用默认参数运行 ga

two_min 辅助函数的代码位于本示例的末尾。使用默认参数运行 ga 以最小化 two_min 函数。使用 gaplot1drange 辅助函数（包含在此示例的末尾）绘制每次迭代时 ga 种群的范围。

rng default % For reproducibility
options = optimoptions('ga','PlotFcn',@gaplot1drange);
[x,fval] = ga(@two_min,1,[],[],[],[],[],[],[],options)
ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

Figure Genetic Algorithm contains an axes object. The axes object with title Range of Population, Mean, xlabel Generation contains an object of type errorbar.

x = 
-0.0688

fval = 
-1.0000

遗传算法返回一个非常接近 x = 0 局部最小值的点。请注意，所有个体都位于 -60 至 60 之间。种群从未探索 x = 101 处全局最小值附近的点。

增加初始范围

使遗传算法探索更大范围的点（即增加种群的多样性）的一种方法是增加初始范围。初始范围不必包含点 x = 101，但它必须足够大，以便算法在 x = 101 附近生成个体。将 InitialPopulationRange 选项设置为 [-10;90] 并重新运行求解器。

options.InitialPopulationRange = [-10;90];
[x,fval] = ga(@two_min,1,[],[],[],[],[],[],[],options)
ga stopped because it exceeded options.MaxGenerations.

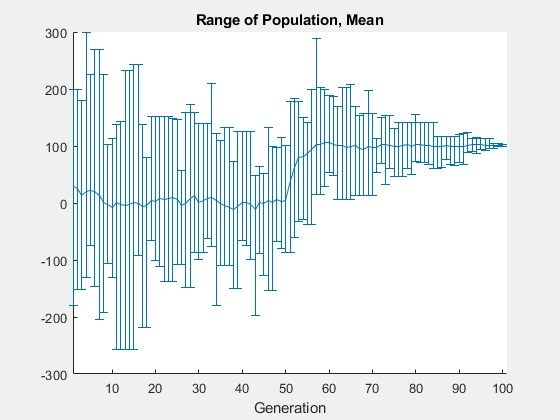
Figure Genetic Algorithm contains an axes object. The axes object with title Range of Population, Mean, xlabel Generation contains an object of type errorbar.

x = 
100.9783

fval = 
-1.3674

这一次，自定义图表展现的个体范围更加广泛。从一开始就有接近 101 的个体，并且种群平均值开始收敛到 101。

辅助函数

以下代码创建 two_min 辅助函数。

function y = two_min(x)
if x <= 100
    y = -exp(-(x/100)^2);
else
    y = -exp(-1) + (x-100)*(x-102);
end
end

以下代码创建 gaplot1drange 辅助函数。

function state = gaplot1drange(options,state,flag)
%gaplot1drange Plots the mean and the range of the population.
%   STATE = gaplot1drange(OPTIONS,STATE,FLAG) plots the mean and the range
%   (highest and the lowest) of individuals (1-D only).  
%
%   Example:
%   Create options that use gaplot1drange
%   as the plot function
%     options = optimoptions('ga','PlotFcn',@gaplot1drange);

%   Copyright 2012-2014 The MathWorks, Inc.

if isinf(options.MaxGenerations) || size(state.Population,2) > 1
    title('Plot Not Available','interp','none');
    return;
end
generation = state.Generation;
score = state.Population;
smean = mean(score);
Y = smean;
L = smean - min(score);
U = max(score) - smean;

switch flag

    case 'init'
        set(gca,'xlim',[1,options.MaxGenerations+1]);
        plotRange = errorbar(generation,Y,L,U);
        set(plotRange,'Tag','gaplot1drange');
        title('Range of Population, Mean','interp','none')
        xlabel('Generation','interp','none')
    case 'iter'
        plotRange = findobj(get(gca,'Children'),'Tag','gaplot1drange');
        newX = [get(plotRange,'Xdata') generation];
        newY = [get(plotRange,'Ydata') Y];
        newL = [get(plotRange,'Ldata') L];
        newU = [get(plotRange,'Udata') U];       
        set(plotRange,'Xdata',newX,'Ydata',newY,'Ldata',newL,'Udata',newU);
end
end

另请参阅

主题