什么是全局优化?
局部最优与全局最优
优化是寻找使函数最小化的点的过程。更具体来说:
函数的局部最小值是函数值小于或等于附近点的值,但可能大于远处点的值的点。
全局最小值是函数值小于或等于所有其他可行点的值的点。
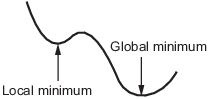
一般来说,Optimization Toolbox™ 求解器会找到局部最优。(这个局部最优可以是全局最优。)它们在起点的吸引盆中找到了最优。有关详细信息,请参阅吸引盆。
相比之下,Global Optimization Toolbox 求解器旨在搜索多个吸引盆。它们用各种方式进行搜索:
GlobalSearch和MultiStart生成许多起点。然后,它们使用局部求解器在起点的吸引盆找到最优解。ga使用一组起点(称为种群),并从种群中迭代生成更好的点。只要初始种群覆盖几个盆地,ga就可以检查几个盆地。particleswarm与ga一样,使用一组起点。particleswarm可以同时检查多个盆地,因为其种群多样化。simulannealbnd执行随机搜索。一般来说,如果一个点比前一个点更好,simulannealbnd就会接受它。simulannealbnd偶尔会接受一个更差的点,以便到达不同的盆地。patternsearch在接受其中一个点之前,会查看多个相邻点。如果一些邻近点属于不同的盆地,patternsearch本质上会同时在多个盆地中查找。surrogateopt首先在边界内进行准随机采样,寻找一个小的目标函数值。surrogateopt使用优化函数,该函数部分地优先考虑远离评估点的点,这是试图达到全局解。在无法改善当前点之后,surrogateopt会重置,导致其再次在边界内进行广泛采样。重置是surrogateopt寻找全局解的另一种方法。
吸引盆
如果目标函数 f(x) 是平滑的,则向量 –∇f(x) 指向 f(x) 下降最快的方向。最陡下降方程,即
产生一条路径 x(t),当 t 变大时,该路径会走向局部最小值。一般来说,彼此接近的初始值 x(0) 会给出趋向于相同最小值点的最陡下降路径。最速下降的吸引盆是导致同一局部最小值的一组初始值。
下图显示了两个一维极小值。图中用不同的线型显示了不同的吸引盆,并用箭头显示了最陡下降的方向。对于此图以及后面的图,黑点表示局部最小值。从 x(0) 点开始,每条最陡下降路径都抵达包含 x(0) 的盆中的黑点。

下图显示了最陡下降路径在更多维度中如何变得更加复杂。

下图显示了更为复杂的路径和吸引盆。

约束可以将一个吸引盆分成几个部分。例如,假设在以下约束条件下求 y 的最小值:
y ≥ |x|
y ≥ 5 – 4(x–2)2.
图中显示了两个吸引盆及其最终点。

最陡下降路径是向下一直延伸到约束边界的直线。从约束边界开始,最陡下降路径沿边界向下行进。最终点是 (0,0) 或 (11/4,11/4),具体取决于初始 x 值是高于还是低于 2。
