Main Content

本页采用了机器翻译。点击此处可查看最新英文版本。

使用 lsqcurvefit 或 lsqnonlin 的 MultiStart

打开实时脚本

此示例显示如何使用 lsqcurvefit 和 MultiStart 来使函数适合数据。示例的末尾展示了使用 lsqnonlin 的相同解。

许多拟合问题都有多个局部解。MultiStart 可以帮助找到全局解，即最佳拟合。本例首先使用 lsqcurvefit，因为它的语法很方便。

模型是

y=a+bx1sin(cx2+d),

其中输入数据为 x=(x1,x2)，参数 a、b、c、d 为未知模型系数。

步骤 1.创建目标函数。

编写一个匿名函数，该函数接受具有 N 行和两列的数据矩阵 xdata，并返回具有 N 行的响应向量。该函数还采用系数矩阵 p，对应系数向量 (a,b,c,d)。 

fitfcn = @(p,xdata)p(1) + p(2)*xdata(:,1).*sin(p(3)*xdata(:,2)+p(4));

步骤 2.创建训练数据。

创建 200 个数据点和响应。使用值 a=-3,b=1/4,c=1/2,d=1。在响应中包含随机噪声。 

rng default % For reproducibility
N = 200; % Number of data points
preal = [-3,1/4,1/2,1]; % Real coefficients

xdata = 5*rand(N,2); % Data points
ydata = fitfcn(preal,xdata) + 0.1*randn(N,1); % Response data with noise

步骤 3.设置边界和初始点。

为 lsqcurvefit 设置边界。d 的绝对值没有理由超过 π，因为正弦函数在任何宽度区间 2π 上都取其整个范围内的值。假设系数 c 的绝对值必须小于 20，因为允许高频率会导致不稳定的响应或不准确的收敛。 

lb = [-Inf,-Inf,-20,-pi];
ub = [Inf,Inf,20,pi];

将初始点任意设置为 (5,5,5,0)。 

p0 = 5*ones(1,4); % Arbitrary initial point
p0(4) = 0; % Ensure the initial point satisfies the bounds

步骤 4.求最佳局部拟合。

将参数与数据拟合，从 p0 开始。 

[xfitted,errorfitted] = lsqcurvefit(fitfcn,p0,xdata,ydata,lb,ub)
Local minimum possible.

lsqcurvefit stopped because the final change in the sum of squares relative to 
its initial value is less than the value of the function tolerance.

xfitted = 1×4

   -2.6149   -0.0238    6.0191   -1.6998


errorfitted = 28.2524

lsqcurvefit 找到一个不是特别接近模型参数值 (-3,1/4,1/2,1) 的局部解。

步骤 5.为 MultiStart 设置问题。

创建一个问题结构体，以便 MultiStart 可以解决同样的问题。 

problem = createOptimProblem('lsqcurvefit','x0',p0,'objective',fitfcn,...
    'lb',lb,'ub',ub,'xdata',xdata,'ydata',ydata);

步骤 6.找到一个全局解。

使用 MultiStart 通过 50 次迭代解决拟合问题。将最小误差绘制为 MultiStart 迭代次数。 

ms = MultiStart('PlotFcns',@gsplotbestf);
[xmulti,errormulti] = run(ms,problem,50)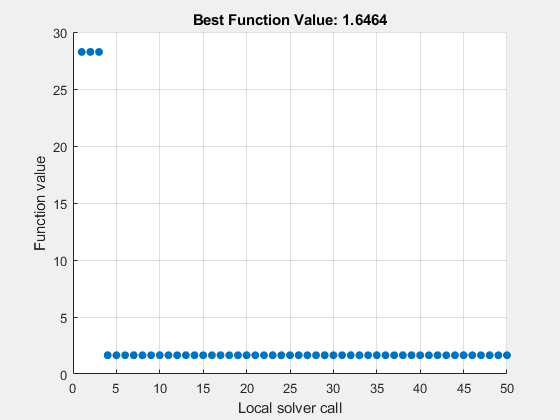

MultiStart completed the runs from all start points. 

All 50 local solver runs converged with a positive local solver exitflag.

xmulti = 1×4

   -2.9852   -0.2472   -0.4968   -1.0438


errormulti = 1.6464

MultiStart 在参数值 (-3,-1/4,-1/2,-1) 附近找到了一个全局解。（这相当于接近 preal = (-3,1/4,1/2,1)的解，因为改变除第一个系数之外的所有系数的符号都会得出相同的 fitfcn 数值。）残差误差的范数从约 28 减少至约 1.6，减少了 10 倍以上。

构建关于 lsqnonlin 的问题

作为替代方法，使用 lsqnonlin 作为拟合函数。在这种情况下，使用预测值和实际数据值之间的差异作为目标函数。

fitfcn2 = @(p)fitfcn(p,xdata)-ydata;
[xlsqnonlin,errorlsqnonlin] = lsqnonlin(fitfcn2,p0,lb,ub)
Local minimum possible.

lsqnonlin stopped because the final change in the sum of squares relative to 
its initial value is less than the value of the function tolerance.

xlsqnonlin = 1×4

   -2.6149   -0.0238    6.0191   -1.6998


errorlsqnonlin = 28.2524

从同一个初始点 p0 出发，lsqnonlin 和 lsqcurvefit 一样找到了相对较差的解。

使用 lsqnonlin 作为局部求解器运行 MultiStart。

problem2 = createOptimProblem('lsqnonlin','x0',p0,'objective',fitfcn2,...
    'lb',lb,'ub',ub');
[xmultinonlin,errormultinonlin] = run(ms,problem2,50)

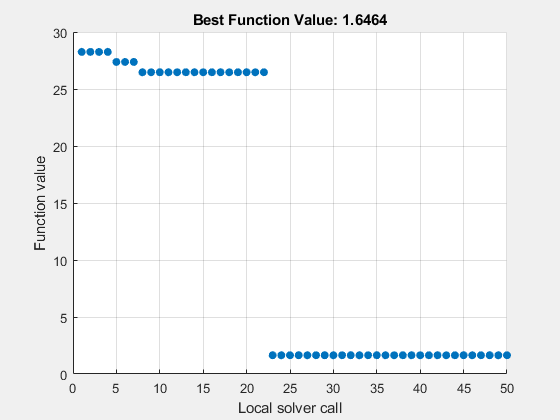
MultiStart completed the runs from all start points. 

All 50 local solver runs converged with a positive local solver exitflag.

xmultinonlin = 1×4

   -2.9852   -0.2472   -0.4968   -1.0438


errormultinonlin = 1.6464

再次，MultiStart 找到了比单独使用局部求解器更好的解。

相关主题