绘制三维帕累托前沿图
此示例说明如何绘制三个目标的帕累托前沿。每个目标函数均为与特定三维点的距离的平方。为了加快计算速度,将每个目标函数以向量化方式编写为点积。为了获得密集解集,使用 200 个帕累托前沿点。
该示例首先显示如何使用内置的 'psplotparetof' 绘图函数获取绘图。然后用 gamultiobj 求解同样的问题并获取绘图,这需要稍微不同的选项设置。此示例说明如何获取帕累托图中特定点的解变量。然后,此示例说明如何在不使用绘图函数的情况下直接绘制点,并说明如何绘制插值曲面而不是帕累托点。
fun = @(x)[dot(x - [1,2,3],x - [1,2,3],2), ... dot(x - [-1,3,-2],x - [-1,3,-2],2), ... dot(x - [0,-1,1],x - [0,-1,1],2)]; options = optimoptions('paretosearch','UseVectorized',true,'ParetoSetSize',200,... 'PlotFcn','psplotparetof'); lb = -5*ones(1,3); ub = -lb; rng default % For reproducibility [x,f] = paretosearch(fun,3,[],[],[],[],lb,ub,[],options);
Pareto set found that satisfies the constraints. Optimization completed because the relative change in the volume of the Pareto set is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 'options.ConstraintTolerance'.

opts = optimoptions('gamultiobj',"PlotFcn","gaplotpareto","PopulationSize",200); [xg,fg] = gamultiobj(fun,3,[],[],[],[],lb,ub,[],opts);
gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.

此图显示的点数比 paretosearch 图少得多。用更大的种群再次求解该问题。
opts.PopulationSize = 400; [xg,fg] = gamultiobj(fun,3,[],[],[],[],lb,ub,[],opts);
gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.
更改视角以更好地匹配 psplotpareto 图。
view(-40,57)

使用工具提示求解点
使用数据提示工具在图中选择一个点。


图中的点的索引为 92。显示点 xg(92,:),其中包含与图示点相关联的解变量。
disp(xg(92,:))
-0.2889 0.0939 0.4980
计算此点处的目标函数值,以查看它是否与显示的值匹配。
disp(fun(xg(92,:)))
11.5544 15.1912 1.5321
创建三维散点图
使用 scatter3 绘制帕累托前沿上的点。
figure subplot(2,2,1) scatter3(f(:,1),f(:,2),f(:,3),'k.'); subplot(2,2,2) scatter3(f(:,1),f(:,2),f(:,3),'k.'); view(-148,8) subplot(2,2,3) scatter3(f(:,1),f(:,2),f(:,3),'k.'); view(-180,8) subplot(2,2,4) scatter3(f(:,1),f(:,2),f(:,3),'k.'); view(-300,8)
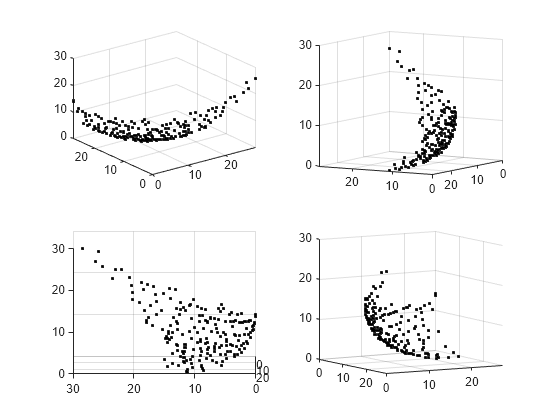
通过以交互方式旋转图,您可以更好地查看其结构。
插值曲面图
要将帕累托前沿视为一个曲面,请创建散点插值。
figure F = scatteredInterpolant(f(:,1),f(:,2),f(:,3),'linear','none');
要绘制生成的曲面,请在 x-y 空间中创建一个从最小值到最大值的网格。然后绘制插值曲面。
sgr = linspace(min(f(:,1)),max(f(:,1))); ygr = linspace(min(f(:,2)),max(f(:,2))); [XX,YY] = meshgrid(sgr,ygr); ZZ = F(XX,YY);
同时绘制帕累托点和曲面。
figure subplot(2,2,1) surf(XX,YY,ZZ,'LineStyle','none') hold on scatter3(f(:,1),f(:,2),f(:,3),'k.'); hold off subplot(2,2,2) surf(XX,YY,ZZ,'LineStyle','none') hold on scatter3(f(:,1),f(:,2),f(:,3),'k.'); hold off view(-148,8) subplot(2,2,3) surf(XX,YY,ZZ,'LineStyle','none') hold on scatter3(f(:,1),f(:,2),f(:,3),'k.'); hold off view(-180,8) subplot(2,2,4) surf(XX,YY,ZZ,'LineStyle','none') hold on scatter3(f(:,1),f(:,2),f(:,3),'k.'); hold off view(-300,8)

通过以交互方式旋转图,您可以更好地查看其结构。
在控制项变量空间中绘制帕累托集
您可以使用 'psplotparetox' 绘图函数获得帕累托集上的点的绘图。
options.PlotFcn = 'psplotparetox';
[x,f] = paretosearch(fun,3,[],[],[],[],lb,ub,[],options);Pareto set found that satisfies the constraints. Optimization completed because the relative change in the volume of the Pareto set is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 'options.ConstraintTolerance'.

或者,创建一个帕累托集中 x 值的散点图。
figure subplot(2,2,1) scatter3(x(:,1),x(:,2),x(:,3),'k.'); subplot(2,2,2) scatter3(x(:,1),x(:,2),x(:,3),'k.'); view(-148,8) subplot(2,2,3) scatter3(x(:,1),x(:,2),x(:,3),'k.'); view(-180,8) subplot(2,2,4) scatter3(x(:,1),x(:,2),x(:,3),'k.'); view(-300,8)

此集没有清晰的曲面。通过以交互方式旋转图,您可以更好地查看其结构。
平行图
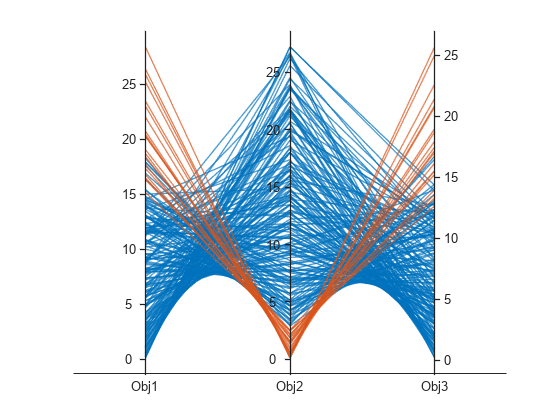
您可以使用平行坐标图绘制帕累托集。可以对任意维数使用平行坐标图。在图中,每条彩色线表示一个帕累托点,每个坐标变量绘制成一条相关联的垂直线。使用 parellelplot 绘制目标函数值。
figure p = parallelplot(f); p.CoordinateTickLabels =["Obj1";"Obj2";"Obj3"];
对 Obj2 的值中最小的十分之一的帕累托点着色。
minObj2 = min(f(:,2));
maxObj2 = max(f(:,2));
grpRng = minObj2 + 0.1*(maxObj2-minObj2);
grpData = f(:,2) <= grpRng;
p.GroupData = grpData;
p.LegendVisible = "off";