优化卫星星座并满足地面站接入约束
此示例显示如何使用带有 Aerospace Toolbox™ 函数的 Global Optimization Toolbox 求解器来查找满足地面站接入要求的最小卫星星座。该示例假设给定一个由四个站组成的地面站网络。更复杂的优化可能包括分配地面站和卫星。访问要求如下:
必须至少在固定百分比的时间内从卫星上观察到几个兴趣点。在这个例子中,兴趣点是地面站。
每颗卫星必须至少以固定百分比的时间观察地面站才能下载数据。您可以使用
accessPercentage(Aerospace Toolbox)函数计算这些百分比。
所有卫星都处于相同的高度,高度是优化变量之一。这些卫星也具有相同的轨道倾角,这是另一个优化变量。卫星位于一定数量的轨道平面上,这是一个优化变量,是一个不超过 10 的整数。最后,每个轨道平面的卫星数量是一个优化变量,是一个不超过 20 的整数。
目标是尽量减少卫星的总数。
星座定义
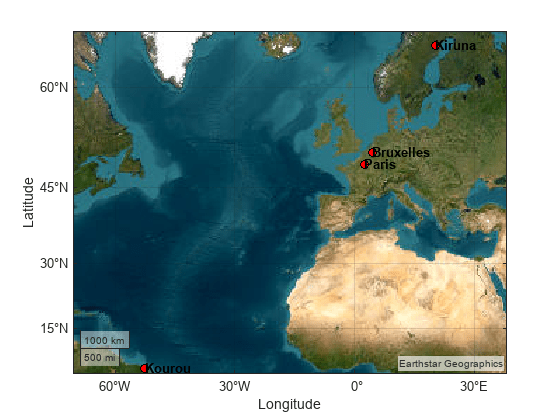
将四个地面站的坐标放置在工作区中。在地图上绘制地面站。
targets = table(... Size=[0,3],... VariableTypes=["string","double","double"],... VariableNames=["Name","Latitude","Longitude"]); targets(1:4,:) = {... "Paris", 48.856614, 2.3522219 ; "Bruxelles", 50.850340, 4.351710 ; "Kiruna", 64.8557995, 20.2252821 ; % Far from the equator "Kourou", 5.1597, -52.6503 }; % Close to the equator figure; geoaxes("Basemap","satellite"); geoplot(targets.Latitude, targets.Longitude,"ko",MarkerFaceColor="red"); % Annotate the targets. text(targets.Latitude,targets.Longitude,targets.Name,FontWeight="bold");
地面站必须至少在 minObservability = 90% 的时间内可以被至少一颗卫星观测到。要计算某个星座是否满足此约束,请使用此示例末尾的 observability 辅助函数。该函数使用卫星场景函数walkerDelta (Aerospace Toolbox)和 Aerospace Toolbox 中可用的访问方法。
minObservability = 0.9;
定义卫星场景并将指定目标作为地面站。将场景和目标对象捆绑到名为 mission 的结构体中。
% Setup scenario mission.Scenario = satelliteScenario(... datetime(2023,09,02,12,0,0),... datetime(2023,09,02,12,0,0) + days(1),... 300); % Ground stations mission.Targets = groundStation(... mission.Scenario,... Name=targets.Name,... Latitude=targets.Latitude,... Longitude=targets.Longitude,... MinElevationAngle=30);
定义一些属于卫星星座定义的量。有关详细信息,请参阅walkerDelta (Aerospace Toolbox)。
phasing = 0;
argLat = 15; % deg优化问题定义
要将该问题表述为优化问题,请定义优化变量,然后根据这些变量定义约束和目标函数。使用基于问题的优化工作流,它提供了一个易于使用的界面来设置优化问题。
优化变量
使用以下变量来解决优化问题:
numPlanes- 轨道平面的数量,从 1 到 10 的整数。satPerPlane- 每个轨道平面的卫星数量,从 1 到 20 的整数。inclination- 倾角以度为单位,从 40 到 80 的实标量。altitude- 以兆米为单位的高度,从 0.5 到 1.2 的实数标量。为了使该变量与其他变量具有大致相同的尺度,请使用兆米,而不是更为熟悉的公里或米。本例末尾的alt2radius辅助函数将高度从兆米转换为米,并在转换中包含地球半径。
使用 optimvar 函数定义优化变量。包括变量类型(整数或连续,如有注明)和边界。
numPlanes = optimvar("numPlanes",Type="integer",LowerBound=1,UpperBound=10); satPerPlane = optimvar("satPerPlane",Type="integer",LowerBound=1,UpperBound=20); inclination = optimvar("inclination",LowerBound=40,UpperBound=80); altitude = optimvar("altitude",LowerBound=0.5,UpperBound=1.2);
目标函数
目标是最小化卫星数量,即每个轨道平面上的卫星数量乘以轨道平面的数量。
创建一个包含该最小化目标函数的优化问题。
satelliteProb = optimproblem(Objective=satPerPlane*numPlanes,ObjectiveSense="minimize");约束
这个问题的约束是
可见性是变量的复杂函数。本示例末尾的 observability 辅助函数计算该数量。要将此辅助函数放入问题中,请使用 fcn2optimexpr 函数将该函数转换为优化表达式。
visibility = fcn2optimexpr(@observability,numPlanes,satPerPlane,mission,...
altitude,inclination,phasing,argLat);将约束添加到优化问题中。
satelliteProb.Constraints = visibility >= minObservability;
检查此问题。
show(satelliteProb)
OptimizationProblem :
Solve for:
altitude, inclination, numPlanes, satPerPlane
where:
numPlanes, satPerPlane integer
minimize :
satPerPlane*numPlanes
subject to :
arg_LHS >= arg_RHS
where:
arg1 = observability(numPlanes, satPerPlane, extraParams{1}, altitude, inclination, 0, 15);
arg_LHS = arg1;
arg2 = 0.9;
arg1 = arg2(ones(1,4));
arg_RHS = arg1(:);
extraParams
variable bounds:
0.5 <= altitude <= 1.2
40 <= inclination <= 80
1 <= numPlanes <= 10
1 <= satPerPlane <= 20
求解问题
问题表示已完成。确定哪些求解器可用于解决该问题。
[default,available] = solvers(satelliteProb)
default = "ga"
available = 1×3 string
"ga" "surrogateopt" "gamultiobj"
对于像这样的耗时、整数约束问题,surrogateopt 求解器通常比默认的 ga 更有效。
使用 surrogateopt 求解器解决问题。为了监控解的进度,请指定 optimplotfvalconstr 绘图函数。为了尝试更快的解,请指定并行计算(需要 Parallel Computing Toolbox™)。为了尝试获得更好的替代模型,请将 MinSurrogatePoints 选项设置为 40,这是默认值的两倍。另外,将函数计算的最大次数设置为 300,比默认值多 100。并行运行时,surrogateopt 不会给出可重现的结果。因此,如果您的执行环境是串行的,请设置随机种子以获得可重现的结果。
rng default % For reproducibility options = optimoptions("surrogateopt",PlotFcn=@optimplotfvalconstr,... UseParallel=true,MaxFunctionEvaluations=300,MinSurrogatePoints=40); [sol,fval,exitflag,output] = solve(satelliteProb,Solver="surrogateopt",Options=options)
Solving problem using surrogateopt.
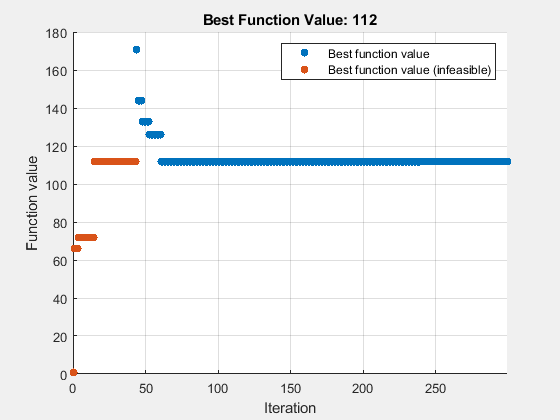
surrogateopt stopped because it exceeded the function evaluation limit set by 'options.MaxFunctionEvaluations'.
sol = struct with fields:
altitude: 1.2000
inclination: 62.8358
numPlanes: 7
satPerPlane: 16
fval = 112
exitflag =
SolverLimitExceeded
output = struct with fields:
elapsedtime: 4.9507e+03
funccount: 300
constrviolation: 3.4602e-04
ineq: [-0.1000 -0.1000 -0.1000 3.4602e-04]
rngstate: [1×1 struct]
message: 'surrogateopt stopped because it exceeded the function evaluation limit set by ↵'options.MaxFunctionEvaluations'.'
solver: 'surrogateopt'
显示解
从优化解中获取单独变量。
numPlanes = sol.numPlanes
numPlanes = 7
numSatPerPlane = sol.satPerPlane
numSatPerPlane = 16
altitudeMm = sol.altitude
altitudeMm = 1.2000
inclination = sol.inclination
inclination = 62.8358
disp("Total number of satellites: " + evaluate(satelliteProb.Objective,sol))Total number of satellites: 112
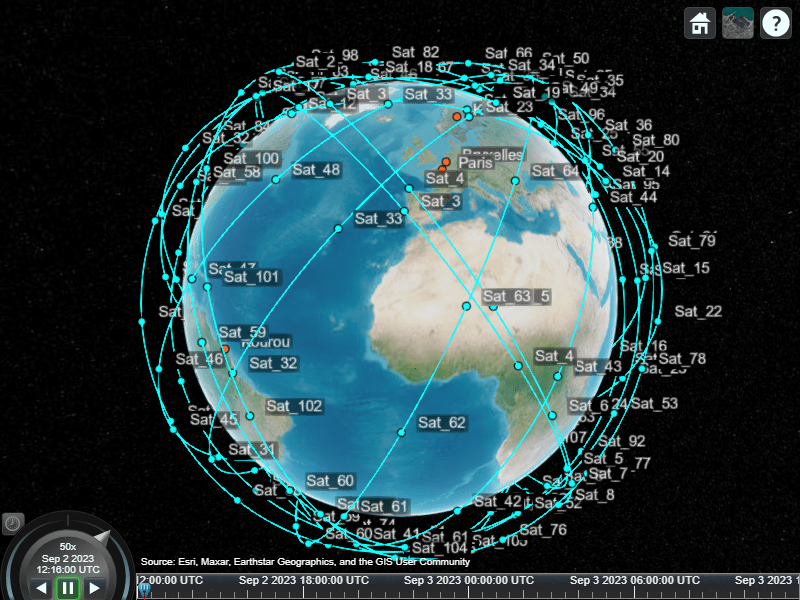
将卫星星座可视化。
radiusMeters = alt2radius(altitudeMm); mission.Constellation = walkerDelta(... mission.Scenario,... radiusMeters,... inclination,... numSatPerPlane*numPlanes,... numPlanes,... phasing,... ArgumentOfLatitude=argLat,... Name="Sat"); satelliteScenarioViewer(mission.Scenario);
辅助函数
使用以下代码创建 alt2radius 函数。
function radiusMeters = alt2radius(altitude) % Convert altitude in Mm to radius in m. % Add the radius of the Earth in Mm. radius = altitude + 6.378137; % Convert the radius to meters. radiusMeters = radius * 1000 * 1000; end
使用以下代码创建 observability 函数。
function targetVisibilityPct = observability(numPlanes,satPerPlane,mission,... altitude,inclination,phasing,argLat) % The radius is in megameters (1000s of km) to keep the optimization search % bounded in [0.5 1.5], which is roughly low Earth orbit. % Convert the radius to meters for walkerDelta setup. radiusMeters = alt2radius(altitude); mission.Constellation = walkerDelta(... mission.Scenario,... radiusMeters,... inclination,... satPerPlane*numPlanes,... numPlanes,... phasing,... ArgumentOfLatitude=argLat,... Name="Sat"); % Compute the access for each target. targetVisibilityPct = zeros(numel(mission.Targets),1); for targetIdx = 1:numel(mission.Targets) accessAnalysis = access(mission.Constellation,mission.Targets(targetIdx)); satAccess = accessStatus(accessAnalysis); systemAccess = any(satAccess,1); targetVisibilityPct(targetIdx) = mean(systemAccess); end end