解决可行性问题

有些问题要求您找到一个满足所有约束的点，而没有目标函数需要最小化。例如，假设您有以下约束：

$\begin{array}{l} (y + x^{2})^{2} + 0.1 y^{2} \leq 1 \\ y \leq \exp (- x) - 3 \\ y \leq x - 4 . \end{array}$

是否有任何点 $(x, y)$ 满足约束？为了找出答案，请编写一个函数，返回结构体字段 Ineq 中的约束。以二元素向量 $x = (x_{1}, x_{2})$ 而不是 $(x, y)$ 的形式写出约束。将每个不等式写成函数 $c (x)$ ，即不等式 $c (x) \leq 0$ ，通过从每个不等式的两边减去其右边。为了能够绘图，请以向量化的方式编写函数，其中每行代表一个点。该辅助函数的代码名为 objconstr，出现在本示例的末尾。

绘制三个函数满足 $- 2 \leq x \leq 2$ 和 $- 4 \leq y \leq 2$ 等式的点，并通过绘制等于 -1/2 的函数值水平线来表示不等式。

[XX,YY] = meshgrid(-2:0.1:2,-4:0.1:2);
ZZ = objconstr([XX(:),YY(:)]).Ineq;
ZZ = reshape(ZZ,[size(XX),3]);
h = figure;
ax = gca;
contour(ax,XX,YY,ZZ(:,:,1),[-1/2 0],'r','ShowText','on');
hold on
contour(ax,XX,YY,ZZ(:,:,2),[-1/2 0],'k','ShowText','on');
contour(ax,XX,YY,ZZ(:,:,3),[-1/2 0],'b','ShowText','on');
hold off

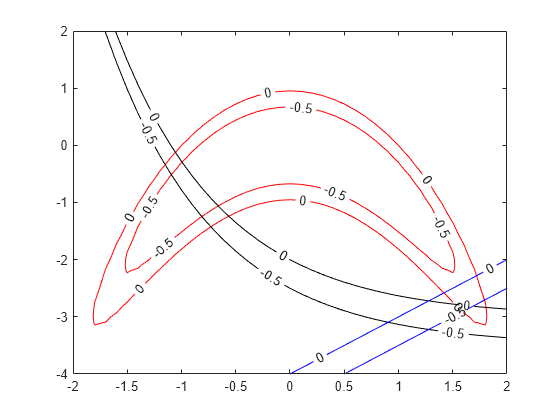
Figure contains an axes object. The axes object contains 3 objects of type contour.

该图表明可行点位于 [1.75,-3] 附近。

设定下界为 -5，上界为 3，然后使用 surrogateopt 解决问题。

rng(1) % For reproducibility
lb = [-5,-5];
ub = [3,3];
[x,fval,exitflag,output,trials] = surrogateopt(@objconstr,lb,ub)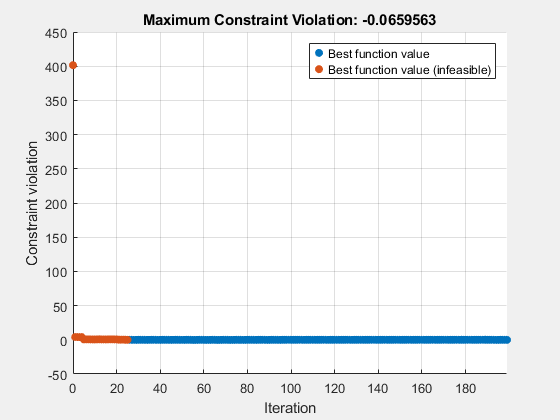

Figure Optimization Plot Function contains an axes object. The axes object with title Maximum Constraint Violation: -0.0659563, xlabel Iteration, ylabel Constraint violation contains 2 objects of type scatter. These objects represent Best function value, Best function value (infeasible).

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

x = 1×2

    1.7553   -3.0551

fval =

  1×0 empty double row vector

exitflag = 
0

output = struct with fields:
        elapsedtime: 39.7959
          funccount: 200
    constrviolation: -0.0660
               ineq: [-0.0660 -0.2280 -0.8104]
           rngstate: [1×1 struct]
            message: 'surrogateopt stopped because it exceeded the function evaluation limit set by ↵'options.MaxFunctionEvaluations'.'

trials = struct with fields:
       X: [200×2 double]
    Ineq: [200×3 double]

检查返回的解 x 的可行性。

disp(output.ineq)

   -0.0660   -0.2280   -0.8104

等效地，在返回的解 objconstr 处评估函数 x。

disp(objconstr(x).Ineq)

   -0.0660   -0.2280   -0.8104

等效地，检查 trials 结构体中的 Ineq 字段以求解 x。首先，在 x 字段中找到 trials.X 的索引。

indx = ismember(trials.X,x,'rows');
disp(trials.Ineq(indx,:))

   -0.0660   -0.2280   -0.8104

所有约束函数值都为负，表明点 x 是可行的。

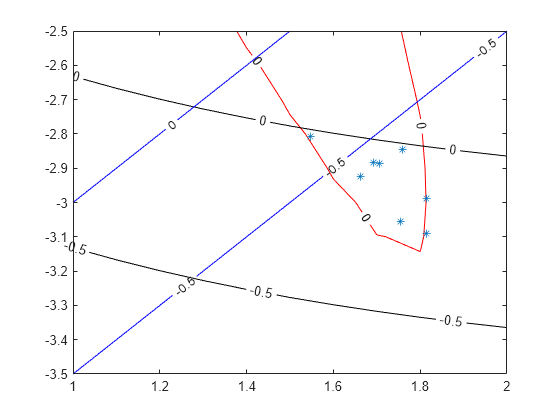
查看由 surrogateopt 评估的可行点。

opts = optimoptions("surrogateopt");
indx = max(trials.Ineq,[],2) <= opts.ConstraintTolerance; % Indices of feasible points
figure(h);
hold on
plot(trials.X(indx,1),trials.X(indx,2),'*')
xlim([1 2])
ylim([-3.5 -2.5])
hold off

Figure contains an axes object. The axes object contains 4 objects of type contour, line. One or more of the lines displays its values using only markers

以下代码创建 objconstr 辅助函数。

function f = objconstr(x)
c(:,1) = (x(:,2) + x(:,1).^2).^2 + 0.1*x(:,2).^2 - 1;
c(:,2) = x(:,2) - exp(-x(:,1)) + 3;
c(:,3) = x(:,2) - x(:,1) + 4;
f.Ineq = c;
end

另请参阅

surrogateopt

解决可行性问题

另请参阅

主题