本页采用了机器翻译。点击此处可查看最新英文版本。

修改 surrogateopt 选项

此示例使用:

打开实时脚本

此示例说明如何通过对具有六个局部极小值的二维问题运行 surrogateopt 来寻找全局最小值。然后，示例展示如何修改一些选项以更有效地搜索。

定义目标函数 sixmin 如下。

sixmin = @(x)(4*x(:,1).^2 - 2.1*x(:,1).^4 + x(:,1).^6/3 ...
    + x(:,1).*x(:,2) - 4*x(:,2).^2 + 4*x(:,2).^4);

绘制函数。

[X,Y] = meshgrid(linspace(-2.1,2.1),linspace(-1.2,1.2));
Z = sixmin([X(:),Y(:)]);
Z = reshape(Z,size(X));
surf(X,Y,Z,'EdgeColor','none')
view(-139,31)

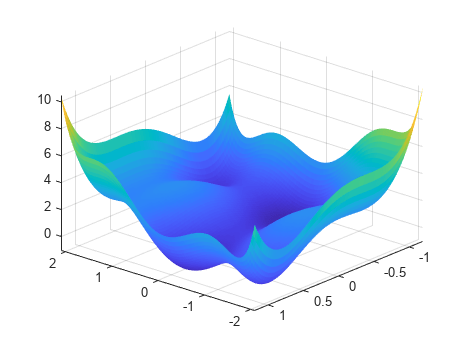
Figure contains an axes object. The axes object contains an object of type surface.

该函数有六个局部极小值和两个全局极小值。

使用 surrogateopt 绘图函数在每个方向由 'surrogateoptplot' 限定的区域中对问题运行 [-2.1,2.1]。要了解 'surrogateoptplot' 图，请参阅 解释 surrogateoptplot。

rng default
lb = [-2.1,-2.1];
ub = -lb;
opts = optimoptions('surrogateopt','PlotFcn','surrogateoptplot');
[xs,fvals,eflags,outputs] = surrogateopt(sixmin,lb,ub,opts);

Figure Optimization Plot Function contains an axes object. The axes object with title Best: -1.03163 Incumbent: -0.805258 Current: 0.0541771, xlabel Number of Function Evaluations, ylabel Objective Function contains 6 objects of type line. One or more of the lines displays its values using only markers These objects represent Best, Incumbent, Random Samples, Adaptive Samples, Surrogate Reset.

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

为 MinSurrogatePoints 选项设置一个较小的值，看看这个变化是否有助于求解器更快地达到全局最小值。

opts.MinSurrogatePoints = 4;
[xs2,fvals2,eflags2,outputs2] = surrogateopt(sixmin,lb,ub,opts);

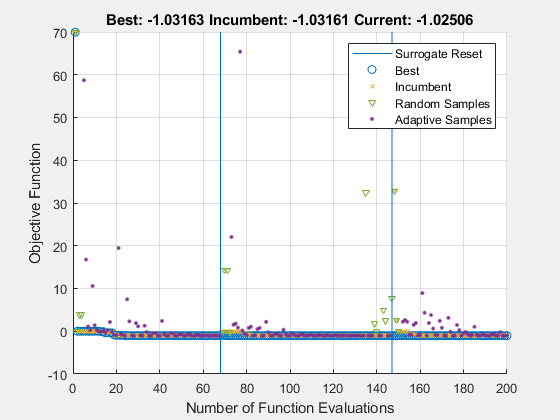
Figure Optimization Plot Function contains an axes object. The axes object with title Best: -1.03163 Incumbent: -1.03161 Current: -1.02506, xlabel Number of Function Evaluations, ylabel Objective Function contains 6 objects of type line. One or more of the lines displays its values using only markers These objects represent Best, Incumbent, Random Samples, Adaptive Samples, Surrogate Reset.

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

较小的 MinSurrogatePoints 选项不会明显改变求解器的行为。

尝试设置 MinSampleDistance 选项的更大值。

opts.MinSampleDistance = 0.05;
[xs3,fvals3,eflags3,outputs3] = surrogateopt(sixmin,lb,ub,opts);

Figure Optimization Plot Function contains an axes object. The axes object with title Best: -0.896062 Incumbent: -0.0401772 Current: 24.5704, xlabel Number of Function Evaluations, ylabel Objective Function contains 12 objects of type line. One or more of the lines displays its values using only markers These objects represent Best, Incumbent, Random Samples, Adaptive Samples, Surrogate Reset.

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

改变 MinSampleDistance 选项对求解器的影响很小。此设置会导致替代更频繁地重置，并导致最佳目标函数比以前略高（更差）。

尝试使用并行处理。对 camelback 函数（sixmin 函数的一个变体）的并行处理和非并行处理的执行进行计时。为了模拟耗时的函数，camelback 函数在每次函数评估时都会增加一秒钟的暂停。

type camelback
function y = camelback(x)

y = (4*x(1)^2 - 2.1*x(1)^4 + x(1)^6/3 ...
    + x(1)*x(2) - 4*x(2)^2 + 4*x(2)^4);
pause(1)

tic
opts = optimoptions('surrogateopt','UseParallel',true,'PlotFcn','surrogateoptplot');
[xs4,fvals4,eflags4,outputs4] = surrogateopt(@camelback,lb,ub,opts);

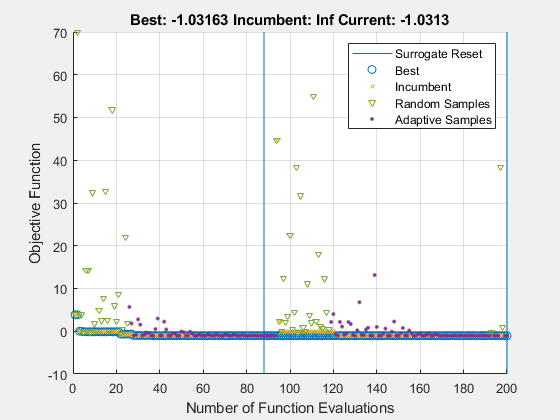
Figure Optimization Plot Function contains an axes object. The axes object with title Best: -1.03163 Incumbent: Inf Current: -1.0313, xlabel Number of Function Evaluations, ylabel Objective Function contains 6 objects of type line. One or more of the lines displays its values using only markers These objects represent Best, Incumbent, Random Samples, Adaptive Samples, Surrogate Reset.

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

toc
Elapsed time is 40.111853 seconds.

当串行运行同一问题时对求解器进行计时。

opts.UseParallel = false;
tic
[xs5,fvals5,eflags5,outputs5] = surrogateopt(@camelback,lb,ub,opts);

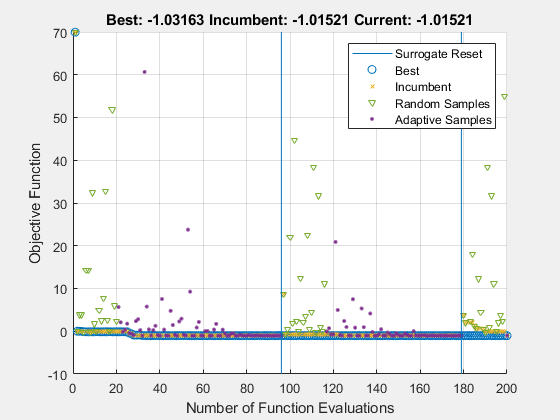
Figure Optimization Plot Function contains an axes object. The axes object with title Best: -1.03163 Incumbent: -1.01521 Current: -1.01521, xlabel Number of Function Evaluations, ylabel Objective Function contains 6 objects of type line. One or more of the lines displays its values using only markers These objects represent Best, Incumbent, Random Samples, Adaptive Samples, Surrogate Reset.

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

toc
Elapsed time is 224.924526 seconds.

对于耗时的目标函数，并行处理可以显著提高速度，且不会过度影响结果。

另请参阅

主题