2-Way Directional Valve (G)

Controlled valve with two ports in a gas network

Libraries:
Simscape / Fluids / Gas / Valves & Orifices / Directional Control Valves

Description

The 2-Way Directional Valve (G) block represents a valve with two ports, A and B, and one flow path, A–B. The path runs through an orifice of variable width. The input signal specified at port S controls the position of the spool. The valve closes when the spool covers the orifice opening.

The flow can be laminar or turbulent, and it can reach up to sonic speeds. The maximum velocity happens at the throat of the valve where the flow is narrowest and fastest. The flow chokes and the velocity saturates when a drop in downstream pressure can no longer increase the velocity. Choking occurs when the back-pressure ratio reaches the critical value characteristic of the valve. The block does not capture supersonic flow.

Valve Positions

The valve is continuously variable and it shifts smoothly between one normal and one working position.

When the instantaneous displacement of the spool at port S is zero, the valve reverts to the normal position where it is no longer operating. Unless the land of the spool is at an offset to the valve orifice, the valve is fully closed. The working position is the position the valve moves to when the spool is maximally displaced, in the positive direction, from the normal position. The orifice is then fully open.

The spool displacement that puts the valve in its working position depends on the offset of the land on the spool. The Valve opening fraction offset parameter specifies the block constant for the spool displacements of the ports.

Orifice Opening Fractions

Between valve positions, the opening of the A–B orifice depends on where the land of the spool is, relative to the rim. This distance is the orifice opening, and the block normalizes this distance so that its value is a fraction of the maximum distance at which the orifice is fully open. The normalized variable is the orifice opening fraction.

The orifice opening fraction can range from 0, in the normal position, to 1, in the working position. The block calculates the opening fractions from the spool displacement and opening fraction offset. The displacement and offset are unitless fractions of the maximum land-orifice distance. The orifice opening fraction is:

$h_{A B} = H_{A B} + x,$

where:

h is the opening fraction of the A–B orifice. If the calculation returns a value outside of the range 0 - 1, the block uses the nearest limit.
H is the value of the Valve opening fraction offset parameter. To allow for unusual valve configurations, the block imposes no limit on their values, although generally these will fall between -1 and +1.
x is the normalized instantaneous displacement of the spool, specified by a physical signal at port S. To compensate for extreme opening fraction offsets, there is no limit on the signal value. The value is typically between 0 and +1.

Opening Fraction Offsets

By default, the valve is fully closed when its control displacement is zero. In this state, the valve is zero-lapped.

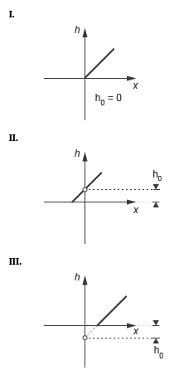
You can offset the lands of the spool to model an underlapped or overlapped valve. Underlapped valves are partially open in the normal position. Overlapped valves are fully closed slightly beyond the normal position. The figure shows how the orifice opening fractions vary with the instantaneous spool displacement:

Image I: A zero-lapped valve. The opening fraction offset is zero. When the valve is in the normal position, the land of the spool completely covers the orifice.
Image II: An underlapped valve. The opening fraction offset is positive. When the valve is in the normal position, the land of the spool partially covers the orifice.
Image III: An overlapped valve. The opening fraction offset is negative. The land of the spool completely covers the orifice not only in the normal position but also over a small region of spool displacements around it.

Control Position in Zero-Lapped, Underlapped, and Overlapped valves

Leakage Flow

The leakage flow ensures that no section of a fluid network becomes isolated. Isolated fluid sections can reduce the numerical robustness of the model, slow the rate of simulation and, in some cases, cause the simulation to fail. The Leakage flow fraction parameter represents the leakage flow area in the block as a small number greater than zero.

Composite Structure

This block is a composite component comprising a single Orifice (G) block connected between ports A, B, and S. Refer to the Orifice (G) block for more detail on the valve parameterizations and block calculations.

Valve Parameterizations

The block behavior depends on the Valve parametrization parameter:

Cv flow coefficient — The flow coefficient C_v determines the block parameterization. The flow coefficient measures the ease with which a gas can flow when driven by a certain pressure differential. [2][3]
Kv flow coefficient — The flow coefficient K_v, where $K_{v} = 0.865 C_{v}$ , determines the block parameterization. The flow coefficient measures the ease with which a gas can flow when driven by a certain pressure differential. [2][3]
Sonic conductance — The sonic conductance of the resistive element at steady state determines the block parameterization. The sonic conductance measures the ease with which a gas can flow when choked, which is a condition in which the flow velocity is at the local speed of sound. Choking occurs when the ratio between downstream and upstream pressures reaches a critical value known as the critical pressure ratio. [1]
Orifice area — The size of the flow restriction determines the block parametrization. [4]

Opening Characteristics

The flow characteristic relates the opening of the valve to the input that produces it, which is often the spool travel. The block expresses the opening as a sonic conductance, flow coefficient, or restriction area, depending on the setting of the Valve parameterization parameter. The control input is the orifice opening fraction, a function of the spool displacement specified at port S.

The flow characteristic is normally given at steady state, with the inlet at a constant, carefully controlled pressure. The flow characteristic depends only on the valve and can be linear or nonlinear. To capture the flow characteristics, use the Opening characteristic parameter:

Linear — The measure of flow capacity is a linear function of the orifice opening fraction. As the opening fraction rises from 0 to 1, the measure of flow capacity scales from the specified minimum to the specified maximum.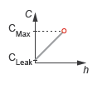
Tabulated — The measure of flow capacity is a general function, which can be linear or nonlinear, of the orifice opening fraction. The function is specified in tabulated form, with the independent variable specified by the Opening fraction vector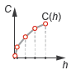

Numerical Smoothing

When the Opening characteristic parameter is Linear, and the Smoothing factor parameter is nonzero, the block applies numerical smoothing to the orifice opening fraction. Enabling smoothing helps maintain numerical robustness in your simulation.

For more information, see Numerical Smoothing.

Assumptions and Limitations

The Sonic conductance setting of the Valve parameterization parameter is for pneumatic applications. If you use this setting for gases other than air, you may need to scale the sonic conductance by the square root of the specific gravity.
The equation for the Orifice area parameterization is less accurate for gases that are far from ideal.
This block does not model supersonic flow.

Ports

Input

expand all

S — Valve control signal, `unitless`
physical signal

Instantaneous displacement of the control member against its normal unactuated position, specified as a physical signal. The block normalizes the displacement against the maximum position of the control member that required to open the orifice fully. The signal is unitless and its instantaneous value is typically in the range between 0 and 1.

Conserving

expand all

A — Valve opening
gas

Gas conserving port associated with the opening through which the flow enters or exits the valve.

B — Valve opening
gas

Gas conserving port associated with the opening through which the flow enters or exits the valve.

Parameters

expand all

Valve parameterization — Parameterization used to specify flow characteristics of orifice
`Cv flow coefficient` (default) | `Kv flow coefficient` | `Sonic conductance` | `Orifice area`

Method to calculate the mass flow rate.

Cv flow coefficient — The flow coefficient C_v determines the block parameterization.
Kv flow coefficient — The flow coefficient K_v, where $K_{v} = 0.865 C_{v}$ , determines the block parameterization.
Sonic conductance — The sonic conductance of the resistive element at steady state determines the block parameterization.
Orifice area — The size of the flow restriction determines the block parametrization.

Opening characteristic — Method to calculate the opening characteristics of the valve
`Linear` (default) | `Tabulated`

Method the block uses to calculate the opening area of the valve. The linear setting treats the opening area as a linear function of the orifice opening fraction. The tabulated setting allows for a general, nonlinear relationship you can specify in tabulated form.

Opening fraction vector — Control signal values at which to specify tabulated parameter data
`0 : 0.2 : 1` (default) | vector of positive numbers

Vector of control signal values at which to specify the chosen measure of flow capacity: Sonic conductance vector, Cv coefficient vector, Kv coefficient vector, or Orifice area vector. The control signal is between 0 and 1, with each value corresponding to an opening fraction of the resistive element. The greater the value, the greater the opening and easier the flow.

The opening fractions must increase monotonically across the vector from left to right. The size of this vector must be the same as the Sonic conductance vector, Cv coefficient vector, Kv coefficient vector, or Orifice area vector parameter.

Dependencies

To enable this parameter, set Opening characteristic to Tabulated.

Maximum Cv flow coefficient — Cv coefficient that corresponds to maximally open component
`4` (default) | positive scalar

Value of the C_v flow coefficient when the restriction area available for flow is at a maximum. This parameter measures the ease with which the gas traverses the resistive element when driven by a pressure differential.

Dependencies

To enable this parameter, set Valve parameterization to Cv flow coefficient, and Opening characteristic to Linear.

xT pressure differential ratio factor at choked flow — Ratio of pressure differentials
`0.7` (default) | positive scalar

Ratio between the inlet pressure, p_in, and the outlet pressure, p_out, defined as $(p_{i n} - p_{o u t}) / p_{i n}$ where choking first occurs. If you do not have this value, look it up in table 2 in ISA-75.01.01 [3]. Otherwise, the default value of 0.7 is reasonable for many valves.

Dependencies

To enable this parameter, set Valve parameterization to Cv flow coefficient or Kv flow coefficient.

Leakage flow fraction — Ratio of flow rates
`1e-6` (default) | positive scalar

Ratio of the flow rate of the orifice when it is closed to when it is open.

Dependencies

To enable this parameter, set Opening characteristic to Linear.

Smoothing factor — Numerical smoothing factor
`0.01` (default) | positive scalar in the range [0,1]

Continuous smoothing factor that introduces a layer of gradual change to the flow response when the orifice is in near-open or near-closed positions. Set this parameter to a nonzero value less than one to increase the stability of your simulation in these regimes.

Dependencies

To enable this parameter, set Opening characteristic to Linear.

Cv flow coefficient vector — Cv coefficients corresponding to values in opening fraction vector
`[1e-06, .8, 1.6, 2.4, 3.2, 4]` (default) | vector of positive numbers

Vector of C_v flow coefficients. Each coefficient corresponds to a value in the Opening fraction vector parameter. This parameter measures the ease with which the gas traverses the resistive element when driven by a pressure differential. The flow coefficients must increase monotonically from left to right, with greater opening fractions representing greater flow coefficients. The size of the vector must be the same as the Opening fraction vector.

Dependencies

To enable this parameter, set Valve parameterization to Cv flow coefficient, and Opening characteristic to Tabulated.

Maximum Kv flow coefficient — Kv coefficient that corresponds to maximally open component
`3.6` (default) | positive scalar

Value of the K_v flow coefficient when the restriction area available for flow is at a maximum. This parameter measures the ease with which the gas traverses the resistive element when driven by a pressure differential.

Dependencies

To enable this parameter, set Valve parameterization to Kv flow coefficient, and Opening characteristic to Linear.

Kv flow coefficient vector — Kv coefficients corresponding to values in opening fraction vector
`[1e-06, .72, 1.44, 2.16, 2.88, 3.6]` (default) | vector of positive numbers

Vector of K_v flow coefficients. Each coefficient corresponds to a value in the Opening fraction vector parameter. This parameter measures the ease with which the gas traverses the resistive element when driven by a pressure differential. The flow coefficients must increase monotonically from left to right, with greater opening fractions representing greater flow coefficients. The size of the vector must be the same as the Opening fraction vector parameter.

Dependencies

To enable this parameter, set Valve parameterization to Kv flow coefficient, and Opening characteristic to Tabulated.

Maximum sonic conductance — Sonic conductance corresponding to maximally open component
`12 l/(bar*s)` (default) | positive scalar

Value of the sonic conductance when the cross-sectional area available for flow is at a maximum.

Dependencies

To enable this parameter, set Valve parameterization to Sonic conductance, and Opening characteristic to Linear.

Critical pressure ratio — Ratio of downstream and upstream pressures at which the flow first chokes
`0.3` (default) | positive scalar

Pressure ratio at which flow first begins to choke and the flow velocity reaches its maximum, given by the local speed of sound. The pressure ratio is the outlet pressure divided by inlet pressure.

Dependencies

To enable this parameter, set Valve parameterization to Sonic conductance, and Opening characteristic to Linear.

Subsonic index — Exponent used to characterize mass flow in subsonic flow regime
`0.5` (default) | positive scalar

Empirical value used to more accurately calculate the mass flow rate in the subsonic flow regime.

Dependencies

To enable this parameter, set Valve parameterization to Sonic conductance.

ISO reference temperature — ISO 8778 reference temperature
`293.15 K` (default) | scalar

Temperature at standard reference atmosphere, defined as 293.15 K in ISO 8778.

You only need to adjust the ISO reference parameter values if you are using sonic conductance values that are obtained at difference reference values.

Dependencies

To enable this parameter, set Valve parameterization to Sonic conductance.

ISO reference density — ISO 8778 reference density
`1.185 kg/m^3` (default) | positive scalar

Density at standard reference atmosphere, defined as 1.185 kg/m3 in ISO 8778.

You only need to adjust the ISO reference parameter values if you are using sonic conductance values that are obtained at difference reference values.

Dependencies

To enable this parameter, set Valve parameterization to Sonic conductance.

Sonic conductance vector — Sonic conductances corresponding to values in opening fraction vector
`[1e-05, 2.4, 4.8, 7.2, 9.6, 12] l/(bar*s)` (default) | vector of positive values

Vector of sonic conductances inside the resistive element. Each conductance corresponds to a value in the Opening fraction vector parameter. The sonic conductances must increase monotonically from left to right, with greater opening fractions representing greater sonic conductances. The size of the vector must be the same as the Opening fraction vector parameter.

Dependencies

To enable this parameter, set Valve parameterization to Sonic conductance, and Opening characteristic to Tabulated.

Critical pressure ratio vector — Critical pressure ratios corresponding to values in opening fraction vector
`0.3 * ones(1,6)` (default) | vector of positive numbers

Vector of critical pressure ratios at which the flow first chokes, with each critical pressure ratio corresponding to a value in the Opening fraction vector parameter. The critical pressure ratio is the fraction of downstream-to-upstream pressures at which the flow velocity reaches the local speed of sound. The size of the vector must be the same as the Opening fraction vector parameter.

Dependencies

To enable this parameter, set Valve parameterization to Sonic conductance, and Opening characteristic to Tabulated.

Maximum orifice area — Flow area corresponding to maximally open component
`1e-4 m^2` (default) | positive scalar

Cross-sectional area of the orifice opening when the cross-sectional area available for flow is at a maximum.

Dependencies

To enable this parameter, set Valve parameterization to Orifice area, and Opening characteristic to Linear.

Discharge coefficient — Discharge coefficient
`0.64` (default) | positive scalar in the range of [0,1]

Correction factor that accounts for discharge losses in theoretical flows.

Dependencies

To enable this parameter, set Valve parameterization to Orifice area.

Orifice area vector — Vector of orifice opening area values
`[1e-10, 2e-05, 4e-05, 6e-05, 8e-05, .0001] m^2` (default) | vector

Vector of cross-sectional areas of the orifice opening. The values in this vector correspond one-to-one with the elements in the Opening fraction vector parameter. The first element of this vector is the orifice leakage area and the last element is the maximum orifice area.

Dependencies

To enable this parameter, set Valve parameterization to Orifice area, and Opening characteristic to Tabulated.

Valve opening fraction offset — Opening fraction of the valve at a zero displacement signal
`0` (default) | unitless scalar

Opening fraction of the valve when the value of the input signal S is zero. The valve is then in the normal position. The opening fraction measures the distance between the land of the spool and the orifice of the valve, normalized by the maximum allowed.

Laminar flow pressure ratio — Pressure ratio at which flow transitions between laminar and turbulent regimes
`0.999` (default) | positive scalar

Pressure ratio at which flow transitions between laminar and turbulent flow regimes. The pressure ratio is the outlet pressure divided by inlet pressure. Typical values range from 0.995 to 0.999.

Cross-sectional area at ports A and B — Flow area at gas ports
`0.01 m^2` (default) | positive scalar

Area normal to the flow path at each port. The ports are equal in size. The value of this parameter should match the inlet area of the components to which the resistive element connects.

References

[1] ISO 6358-3. "Pneumatic fluid power – Determination of flow-rate characteristics of components using compressible fluids – Part 3: Method for calculating steady-state flow rate characteristics of systems". 2014.

[2] IEC 60534-2-3. "Industrial-process control valves – Part 2-3: Flow capacity – Test procedures". 2015.

[3] ANSI/ISA-75.01.01. "Industrial-Process Control Valves – Part 2-1: Flow capacity – Sizing equations for fluid flow underinstalled conditions". 2012.

[4] P. Beater. Pneumatic Drives. Springer-Verlag Berlin Heidelberg. 2007.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2018b

expand all

R2022b: Model gas systems using improved flow computations

In previous versions, the blocks in the gas library used a conversion factor to implement different orifice parameterizations in terms of sonic conductance. You can use the Valve parameterization parameter to specify the parameterization.

The new parameterizations also include new parameters:

xT pressure differential ratio factor at choked flow
Discharge coefficient
Leakage flow fraction. This parameter replaces the Cv coefficient (USCS) at leakage flow, Kv coefficient (SI) at leakage flow, Sonic conductance at leakage flow, and Restriction area at leakage flow parameters.

To improve clarity:

The Opening parameterization parameter has been renamed to Opening characteristic.
The Reference temperature and Reference density parameters have been renamed to ISO reference temperature and ISO reference density, respectively.
The Cv coefficient (USCS) at maximum flow and Kv coefficient (USCS) at maximum flow parameters have been renamed to Maximum Cv coefficient and Maximum Kv coefficient , respectively.
The Sonic conductance at maximum flow parameter has been renamed to Maximum sonic conductance.

2-Way Directional Valve (G)

Description

Valve Positions

Valve Parameterizations

Opening Characteristics

Numerical Smoothing

Assumptions and Limitations

Ports

Input

S — Valve control signal, unitless physical signal

Conserving

A — Valve opening gas

B — Valve opening gas

Parameters

Valve parameterization — Parameterization used to specify flow characteristics of orifice Cv flow coefficient (default) | Kv flow coefficient | Sonic conductance | Orifice area

Opening characteristic — Method to calculate the opening characteristics of the valve Linear (default) | Tabulated

Opening fraction vector — Control signal values at which to specify tabulated parameter data 0 : 0.2 : 1 (default) | vector of positive numbers

Dependencies

Maximum Cv flow coefficient — Cv coefficient that corresponds to maximally open component 4 (default) | positive scalar

Dependencies

xT pressure differential ratio factor at choked flow — Ratio of pressure differentials 0.7 (default) | positive scalar

Dependencies

Leakage flow fraction — Ratio of flow rates 1e-6 (default) | positive scalar

Dependencies

Smoothing factor — Numerical smoothing factor 0.01 (default) | positive scalar in the range [0,1]

Dependencies

Cv flow coefficient vector — Cv coefficients corresponding to values in opening fraction vector [1e-06, .8, 1.6, 2.4, 3.2, 4] (default) | vector of positive numbers

Dependencies

Maximum Kv flow coefficient — Kv coefficient that corresponds to maximally open component 3.6 (default) | positive scalar

Dependencies

Kv flow coefficient vector — Kv coefficients corresponding to values in opening fraction vector [1e-06, .72, 1.44, 2.16, 2.88, 3.6] (default) | vector of positive numbers

Dependencies

Maximum sonic conductance — Sonic conductance corresponding to maximally open component 12 l/(bar*s) (default) | positive scalar

Dependencies

Critical pressure ratio — Ratio of downstream and upstream pressures at which the flow first chokes 0.3 (default) | positive scalar

Dependencies

Subsonic index — Exponent used to characterize mass flow in subsonic flow regime 0.5 (default) | positive scalar

Dependencies

ISO reference temperature — ISO 8778 reference temperature 293.15 K (default) | scalar

Dependencies

ISO reference density — ISO 8778 reference density 1.185 kg/m^3 (default) | positive scalar

Dependencies

Sonic conductance vector — Sonic conductances corresponding to values in opening fraction vector [1e-05, 2.4, 4.8, 7.2, 9.6, 12] l/(bar*s) (default) | vector of positive values

Dependencies

Critical pressure ratio vector — Critical pressure ratios corresponding to values in opening fraction vector 0.3 * ones(1,6) (default) | vector of positive numbers

Dependencies

Maximum orifice area — Flow area corresponding to maximally open component 1e-4 m^2 (default) | positive scalar

Dependencies

Discharge coefficient — Discharge coefficient 0.64 (default) | positive scalar in the range of [0,1]

Dependencies

Orifice area vector — Vector of orifice opening area values [1e-10, 2e-05, 4e-05, 6e-05, 8e-05, .0001] m^2 (default) | vector

Dependencies

Valve opening fraction offset — Opening fraction of the valve at a zero displacement signal 0 (default) | unitless scalar

Laminar flow pressure ratio — Pressure ratio at which flow transitions between laminar and turbulent regimes 0.999 (default) | positive scalar

Cross-sectional area at ports A and B — Flow area at gas ports 0.01 m^2 (default) | positive scalar

References

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using Simulink® Coder™.

Version History

R2022b: Model gas systems using improved flow computations

See Also

S — Valve control signal, `unitless`
physical signal

A — Valve opening
gas

B — Valve opening
gas

Valve parameterization — Parameterization used to specify flow characteristics of orifice
`Cv flow coefficient` (default) | `Kv flow coefficient` | `Sonic conductance` | `Orifice area`

Opening characteristic — Method to calculate the opening characteristics of the valve
`Linear` (default) | `Tabulated`

Opening fraction vector — Control signal values at which to specify tabulated parameter data
`0 : 0.2 : 1` (default) | vector of positive numbers

Maximum Cv flow coefficient — Cv coefficient that corresponds to maximally open component
`4` (default) | positive scalar

xT pressure differential ratio factor at choked flow — Ratio of pressure differentials
`0.7` (default) | positive scalar

Leakage flow fraction — Ratio of flow rates
`1e-6` (default) | positive scalar

Smoothing factor — Numerical smoothing factor
`0.01` (default) | positive scalar in the range [0,1]

Cv flow coefficient vector — Cv coefficients corresponding to values in opening fraction vector
`[1e-06, .8, 1.6, 2.4, 3.2, 4]` (default) | vector of positive numbers

Maximum Kv flow coefficient — Kv coefficient that corresponds to maximally open component
`3.6` (default) | positive scalar

Kv flow coefficient vector — Kv coefficients corresponding to values in opening fraction vector
`[1e-06, .72, 1.44, 2.16, 2.88, 3.6]` (default) | vector of positive numbers

Maximum sonic conductance — Sonic conductance corresponding to maximally open component
`12 l/(bar*s)` (default) | positive scalar

Critical pressure ratio — Ratio of downstream and upstream pressures at which the flow first chokes
`0.3` (default) | positive scalar

Subsonic index — Exponent used to characterize mass flow in subsonic flow regime
`0.5` (default) | positive scalar

ISO reference temperature — ISO 8778 reference temperature
`293.15 K` (default) | scalar

ISO reference density — ISO 8778 reference density
`1.185 kg/m^3` (default) | positive scalar

Sonic conductance vector — Sonic conductances corresponding to values in opening fraction vector
`[1e-05, 2.4, 4.8, 7.2, 9.6, 12] l/(bar*s)` (default) | vector of positive values

Critical pressure ratio vector — Critical pressure ratios corresponding to values in opening fraction vector
`0.3 * ones(1,6)` (default) | vector of positive numbers

Maximum orifice area — Flow area corresponding to maximally open component
`1e-4 m^2` (default) | positive scalar

Discharge coefficient — Discharge coefficient
`0.64` (default) | positive scalar in the range of [0,1]

Orifice area vector — Vector of orifice opening area values
`[1e-10, 2e-05, 4e-05, 6e-05, 8e-05, .0001] m^2` (default) | vector

Valve opening fraction offset — Opening fraction of the valve at a zero displacement signal
`0` (default) | unitless scalar

Laminar flow pressure ratio — Pressure ratio at which flow transitions between laminar and turbulent regimes
`0.999` (default) | positive scalar

Cross-sectional area at ports A and B — Flow area at gas ports
`0.01 m^2` (default) | positive scalar

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.