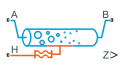
3-Zone Pipe (2P)

Pipe with phase-changing fluid in a two-phase fluid network

Libraries:
Simscape / Fluids / Two-Phase Fluid / Pipes & Fittings

Description

The 3-Zone Pipe (2P) block models a pipe with a phase-changing fluid. Each fluid phase is called a zone, which is a fractional value between 0 and 1. Zones do not mix. The block uses a boundary-following model to track the sub-cooled liquid (L), vapor-liquid mixture (M), and super-heated vapor (V) in three zones. The relative amount of space a zone occupies in the system is called a zone length fraction within the system.

Port H is a thermal port that represents the environmental temperature. The rate of heat transfer between the fluid and the environment depends on the fluid phase of each zone. The block models the pipe wall and the pipe wall temperature in each zone may be different. The fluid dynamic compressibility and the fluid zone thermal capacity impact the fluid pressure and temperature.

Heat Transfer Between the Fluid and the Wall

The convective heat transfer coefficient between the fluid and the wall, α_F, varies per zone according to the Nusselt number

$α_{F} = \frac{Nu k}{D_{H}},$

where:

Nu is the zone Nusselt number.
k the average fluid thermal conductivity.
D_H is the value of the Hydraulic diameter parameter, the equivalent diameter of a non-circular pipe.

The Nusselt number used in the heat transfer coefficient is the greater of the turbulent- and laminar-flow Nusselt numbers.

For turbulent flows in the subcooled liquid or superheated vapor zones, the Nusselt number is calculated with the Gnielinski correlation

$Nu = \frac{\frac{f}{8} (Re - 1000) Pr}{1 + 12.7 {(\frac{f}{8})}^{1 / 2} ({Pr}_{}^{2 / 3} - 1)},$

where:

Re is the zone average Reynolds number.
Pr is the zone average Prandtl number.
f is the Darcy friction factor, calculated from the Haaland correlation

$\frac{1}{\sqrt{f}} = - 1.8 {log}_{10} [{(\frac{\frac{ε}{D_{H}}}{3.7})}^{1.11} + \frac{6.9}{Re}],$
where ε is the value of the Internal surface absolute roughnessparameter.

For turbulent flows in the liquid-vapor mixture zone, the Nusselt number is calculated with the Cavallini-Zecchin correlation

$Nu = \frac{{aRe}_{SL}^{b} {Pr}_{SL}^{c} {{[(\sqrt{\frac{ρ_{SL}}{ρ_{SV}}} - 1) x_{Out} + 1]}^{1 + b} - {[(\sqrt{\frac{ρ_{SL}}{ρ_{SV}}} - 1) x_{In} + 1]}^{1 + b}}}{(1 + b) (\sqrt{\frac{ρ_{SL}}{ρ_{SV}}} - 1) (x_{Out} - x_{In})},$

where:

Re_SL is the Reynolds number of the saturated liquid.
Pr_SL is the Prandtl number of the saturated liquid.
ρ_SL is the density of the saturated liquid.
ρ_SV is the density of the saturated vapor.
a= 0.05, b = 0.8, and c= 0.33.

When fins are modeled on the pipe internal surface, the heat transfer coefficient is

$α_{F} = \frac{Nu k}{D_{H}} (1 + η_{Int} s_{Int}),$

where:

η_Int is the value of the Internal fin efficiency parameter.
s_Int is the value of the Ratio of internal fins surface area to no-fin surface area parameter.

For laminar flows, the Nusselt number is the value of the Laminar flow Nusselt number parameter.

Empirical Nusselt Number Formulation

When the Heat transfer coefficient model parameter is Colburn equation, the block calculates the Nusselt number for the subcooled liquid and superheated vapor zones by using the empirical Colburn equation

$Nu = a {Re}^{b} {Pr}^{c},$

where a, b, and c are values in the Coefficients [a, b, c] for a*Re^b*Pr^c in liquid zone and Coefficients [a, b, c] for a*Re^b*Pr^c in vapor zone parameters.

The block calculates the Nusselt number for liquid-vapor mixture zones by using the Cavallini-Zecchin equation with the variables in the Coefficients [a, b, c] for a*Re^b*Pr^c in mixture zone parameter.

Specific Enthalpy

The heat transfer rate from the fluid is based on the change in specific enthalpy in each zone

$Q = {\dot{m}}_{Q} (Δ h_{L} + Δ h_{M} + Δ h_{V}),$

where ${\dot{m}}_{Q}$ is the mass flow rate for heat transfer. It is the pipe inlet mass flow rate, either $\dot{m}$ _A or $\dot{m}$ _B, depending on the direction of fluid flow.

In the liquid and vapor zones, the change in specific enthalpy is defined as

$Δ h = c_{p} (T_{H} - T_{I}) [1 - exp (- \frac{z S_{W}}{{\dot{m}}_{Q} c_{p} (α_{F}^{- 1} + α_{E}^{- 1})})],$

where:

c_p is the specific heat of the liquid or vapor.
T_H is the environmental temperature.
T_I is the liquid inlet temperature.
z is the fluid zone length fraction.
α_E is the heat transfer coefficient between the wall and the environment.
S_W is wall surface area

$S_{W} = \frac{4 A}{D_{H}} L,$
where:
- A is the value of the Cross-sectional area parameter.
- L is the value of the Pipe length parameter.
The wall surface area does not include fin area, which is set by the Ratio of external fins surface area to no-fin surface area and Ratio of internal fins surface area to no-fin surface area parameters. Fins are set in proportion to the wall surface area. A value of 0 means there are no fins on the pipe wall.

In the liquid-vapor mixture zone, the change in specific enthalpy is calculated as

$Δ h = (T_{H} - T_{S}) \frac{z S_{W}}{{\dot{m}}_{Q} (α_{F}^{- 1} + α_{E}^{- 1})},$

where T_S is the fluid saturation temperature. It is assumed that the liquid-vapor mixture is always at this temperature.

Heat Transfer Rate

The total heat transfer between the fluid and the pipe wall is the sum of the heat transfer in each fluid phase

$Q_{F} = Q_{F,L} + Q_{F,V} + Q_{F,M} .$

The heat transfer rate between the fluid and the pipe in the liquid zone is

$Q_{F,L} = {\dot{m}}_{Q} c_{p,L} [T_{W,L} - min (T_{I}, T_{S})] [1 - exp (- \frac{z_{L} S_{W} α_{L}}{{\dot{m}}_{Q} c_{p,L}})] .$

where T_W,L is the temperature of the wall surrounding the liquid zone.

The heat transfer rate between the fluid and the pipe in the mixture zone is

$Q_{F,M} = (T_{H} - T_{Sat}) z_{M} S_{W} α_{M} .$

The heat transfer rate between the fluid and the pipe in the vapor zone is

$Q_{F,V} = {\dot{m}}_{Q} c_{p,V} [T_{W,V} - min (T_{I}, T_{Sat})] [1 - exp (- \frac{z_{V} S_{W} α_{V}}{{\dot{m}}_{Q} c_{p,V}})],$

where T_W,V is the temperature of the wall surrounding the vapor zone.

Heat Transfer Between the Wall and the Environment

If the pipe wall has a finite thickness, the heat transfer coefficient between the wall and the environment, α_E, is defined by

$\frac{1}{α_{E}} = \frac{1}{α_{W}} + \frac{1}{α_{Ext} (1 + η_{Ext} s_{Ext})},$

where α_W is the heat transfer coefficient due to conduction through the wall

$α_{W} = \frac{k_{W}}{D_{H} ln (1 + \frac{t_{W}}{D_{H}})},$

and where:

k_W is the value of the Wall thermal conductivity parameter.
t_W is the value of the Wall thickness parameter.
α_Ext is the value of the External environment heat transfer coefficient parameter.
η_Ext is the value of the External fin efficiency parameter.
s_Ext is the value of the Ratio of external fins surface area to no-fin surface area parameter.

If the wall does not have thermal mass, the heat transfer coefficient between the wall and environment equals the heat transfer coefficient of the environment, α_Ext.

Heat Transfer Rate

The heat transfer rate between each wall zone and the environment is

$Q_{H,zone} = (T_{H} - T_{W}) z S_{W} α_{E} .$

The total heat transfer between the wall and the environment is

$Q_{H} = Q_{H,L} + Q_{H,V} + Q_{H,M} .$

Governing Differential Equations

The heat transfer rate depends on the thermal mass of the wall, C_W

$C_{W} = c_{p,W} ρ_{W} S_{W} (t_{W} + \frac{t_{W}^{2}}{D_{H}}),$

where:

c_p,W is the value of the Wall specific heat parameter.
ρ_W is the value of the Wall density parameter.

The governing equations for heat transfer between the fluid and the external environment for the liquid zone are

$Q_{H,L} - Q_{F,L} = C_{W} [z_{L} \frac{d T_{W,L}}{d t} + max (\frac{d z_{L}}{d t}, 0) (T_{W,L} - T_{W,M})],$

for the mixture zone are

$Q_{H,M} - Q_{F,M} = C_{W} [z_{M} \frac{d T_{W,M}}{d t} + min (\frac{d z_{L}}{d t}, 0) (T_{W,L} - T_{W,M}) + min (\frac{d z_{V}}{d t}, 0) (T_{W,V} - T_{W,M})],$

and for the vapor zone are

$Q_{H,V} - Q_{F,V} = C_{W} [z_{V} \frac{d T_{W,V}}{d t} + max (\frac{d z_{V}}{d t}, 0) (T_{W,V} - T_{W,M})] .$

Momentum Balance

Two factors determine the pressure differential over the pipe: the changes in pressure due to changes in density, and changes in pressure due to friction at the pipe walls.

For turbulent flows, when the Reynolds number is above the value of the Turbulent flow lower Reynolds number limit parameter, the block calculates the pressure loss in terms of the Darcy friction factor. The pressure differential between port A and the internal node I is

$p_{A} - p_{I} = (\frac{1}{ρ_{I}} - \frac{1}{ρ_{A}^{*}}) {(\frac{{\dot{m}}_{A}}{S})}^{2} + \frac{f_{A} {\dot{m}}_{A} | {\dot{m}}_{A} |}{2 ρ_{I} D_{H} S^{2}} (\frac{L + L_{Add}}{2}) + \frac{Δ p_{h y d r o s t a t i c}}{2},$

where:

ρ_I is the fluid density at internal node I.
ρ_A* is the fluid density at port A, which is the same as ρ_A when the flow is steady-state. When the flow is transient, the block calculates ρ_A* from the fluid internal state at the internal node I with the adiabatic expression

$u_{A}^{*} + \frac{p_{A}}{ρ_{A}^{*}} + \frac{1}{2} {(\frac{{\dot{m}}_{A}}{ρ_{A}^{*} S})}^{2} = h + \frac{1}{2} {(\frac{{\dot{m}}_{A}}{ρ S})}^{2},$
where:
- h is the average specific enthalpy, $h = h_{L} z_{L} + h_{V} z_{V} + h_{M} z_{M} .$
- ρ is the average density, $ρ = ρ_{L} z_{L} + ρ_{M} z_{M} + ρ_{V} z_{V} .$
$\dot{m}$ _A is the mass flow rate through port A.
L is the value of the Pipe length parameter.
L_Add is the value of the Aggregate equivalent length of local resistances parameter, which is the equivalent length of a tube that introduces the same amount of loss as the sum of the losses due to other local resistances.
$Δ p_{h y d r o s t a t i c} = \frac{M}{V} g Δ z$ is the hydrostatic pressure, where:
- M is the total fluid mass in the pipe.
- V is the total fluid volume which is the volume of the pipe.
- g is the value of the Gravitational acceleration parameter.
- Δz is the value of the Elevation gain from port A to port B parameter.

The Darcy friction factor depends on the Reynolds number, which the block calculates at both ports.

The pressure differential between port B and internal node I is

$p_{B} - p_{I} = (\frac{1}{ρ_{I}} - \frac{1}{ρ_{B}^{*}}) {(\frac{{\dot{m}}_{B}}{S})}^{2} + \frac{f_{B} {\dot{m}}_{B} | {\dot{m}}_{B} |}{2 ρ_{I} D_{H} S_{}^{2}} (\frac{L + L_{Add}}{2}) - \frac{Δ p_{h y d r o s t a t i c}}{2},$

where:

ρ_B* is the fluid density at port B, which is the same as ρ_B when the flow is steady-state. When the flow is transient, the block calculates ρ_B* from the fluid internal state with the adiabatic expression

$u_{B}^{*} + \frac{p_{B}}{ρ_{B}^{*}} + \frac{1}{2} {(\frac{{\dot{m}}_{B}}{ρ_{B}^{*} S})}^{2} = h + \frac{1}{2} {(\frac{{\dot{m}}_{B}}{ρ S})}^{2} .$
$\dot{m}$ _B is the mass flow rate through port B.

For laminar flows, when the Reynolds number is below the value of the Laminar flow upper Reynolds number limit parameter, the block calculates the pressure loss due to friction in terms of the Laminar friction constant for Darcy friction factor parameter, λ. The pressure differential between port A and internal node I is

$p_{A} - p_{I} = (\frac{1}{ρ_{I}} - \frac{1}{ρ_{A}^{*}}) {(\frac{{\dot{m}}_{A}}{S})}^{2} + \frac{λ μ {\dot{m}}_{A}}{2 ρ_{I} D_{H}^{2} S} (\frac{L + L_{Add}}{2}) + \frac{Δ p_{h y d r o s t a t i c}}{2},$

where μ is the average fluid dynamic viscosity

$μ = μ_{L} z_{L} + μ_{M} z_{M} + μ_{V} z_{V} .$

The pressure differential between port B and internal node I is

$p_{B} - p_{I} = (\frac{1}{ρ_{I}} - \frac{1}{ρ_{B}^{*}}) {(\frac{{\dot{m}}_{B}}{S})}^{2} + \frac{λ μ {\dot{m}}_{B}}{2 ρ_{I} D_{H}^{2} S} (\frac{L + L_{Add}}{2}) - \frac{Δ p_{h y d r o s t a t i c}}{2} .$

For transitional flows, the block smooths the pressure differential due to viscous friction between the values for laminar and turbulent pressure losses.

Mass Balance

The total mass accumulation rate is

$\frac{d M}{d t} = {\dot{m}}_{A} + {\dot{m}}_{B} .$

In terms of the fluid zones, the mass accumulation rate is a function of the change in density, ρ, with respect to pressure, p, and the fluid specific internal energy, u

$\frac{d M}{d t} = [{(\frac{\partial ρ}{\partial p})}_{u} \frac{d p}{d t} + {(\frac{\partial ρ}{\partial u})}_{p} \frac{d u_{o u t}}{d t} + ρ_{L} \frac{d z_{L}}{d t} + ρ_{M} \frac{d z_{M}}{d t} + ρ_{V} \frac{d z_{V}}{d t}] V,$

where u_out is the specific internal energy after all heat transfer has occurred.

Energy Balance

The energy conservation equation is

$M \frac{d u_{o u t}}{d t} + ({\dot{m}}_{A} + {\dot{m}}_{B}) u_{o u t} = ϕ_{A} + ϕ_{B} + Q_{F} - {\dot{m}}_{a v g} g Δ z,$

where:

ϕ_A is the energy flow rate at port A.
ϕ_B is the energy flow rate at port B.
Q_F is the heat transfer rate between the fluid and the wall.
${\dot{m}}_{a v g} = \frac{{\dot{m}}_{A} - {\dot{m}}_{B}}{2} .$

Assumptions and Limitations

The pipe wall is perfectly rigid.
The flow is fully developed. Friction losses and heat transfer do not include entrance effects.
Fluid inertia is negligible.
The block models gravitational effects at a bulk-system level and does not model the separation of liquid and vapor within the pipe due to gravity.
When the pressure is above the fluid critical pressure, large values of thermal fluid properties (such as Prandtl number, thermal conductivity, and specific heat) may not accurately reflect the heat exchange in the pipe.

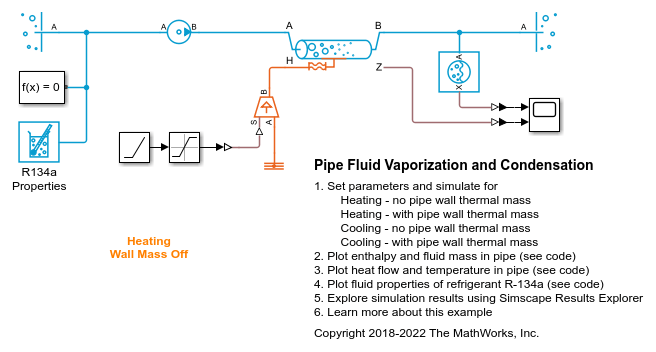
Examples

Pipe Fluid Vaporization and Condensation

The 3-Zone Pipe (2P) block used to model vaporization or condensation of fluid flow in a pipe. The block divides the internal fluid volume into up to three zones: liquid zone, mixture zone, and vapor zone, depending on the state of the fluid along the pipe. As fluid flows through the pipe, heat is transferred between the environment external to the pipe and the fluid inside the pipe, causing it to change from liquid to mixture to vapor for the heating case or from vapor to mixture to liquid for the cooling case. The effect of thermal storage in the pipe wall can be optionally turned on by specifying a nonzero pipe wall thickness.

Open Model

Ports

Output

expand all

Z — Zone length fractions
physical signal

Vector with the length fractions of the liquid, mixed-phase, and vapor zones in the pipe.

Conserving

expand all

A — Pipe opening
two-phase fluid

Opening through which the two-phase fluid flows into or out of the pipe. Ports A and B can each function as either inlet or outlet. Thermal conduction is allowed between the two-phase fluid ports and the fluid internal to the pipe (though its impact is typically relevant only at near zero flow rates).

B — Pipe opening
two-phase fluid

H — Pipe wall
thermal

Thermal boundary condition at the outer surface of the pipe wall. Use this port to capture heat exchange of various kinds—for example, conductive, convective, or radiative—between the pipe wall and the environment. Heat exchange between the inner surface of the wall and the fluid is captured directly in the block.

Parameters

expand all

Geometry

Pipe length — Distance between the ports of the pipe
`5 m` (default) | positive scalar with units of length

Distance between the ports of the pipe. The liquid, two-phase, and vapor zones each comprise a fraction of this distance. The zone fractions can vary but their aggregate length, being the same as the distance of the pipe, is fixed.

Cross-sectional area — Internal area normal to the direction of the flow
`0.01 m^2` (default) | positive scalar with units of area

Internal area of the pipe normal to the direction of flow. The cross section of the pipe is assumed to be constant throughout its length.

Hydraulic diameter — Diameter of a cylindrical pipe with the given cross-sectional area
`0.1 m` (default) | positive scalar in units of length

Ratio of the opening area of a cross section of the pipe to the perimeter of that area. The pipe is not required to be cylindrical, and its cross-section have any shape. This parameter gives the diameter that a general cross section would have if it were circular.

Elevation gain from port A to port B — Constant pipe elevation differential
`0 m` (default) | scalar

Elevation differential for across the pipe.

Gravitational acceleration — Gravitational acceleration
`9.81 m/s^2` (default) | scalar

Gravitational acceleration in the pipe environment.

Viscous Friction

Aggregate equivalent length of local resistances — Minor pressure loss in the pipe expressed as a length
`1 m` (default) | positive scalar in units of length

Combined length of all local resistances present in the pipe. Local resistances include bends, fittings, armatures, and pipe inlets and outlets. The effect of the local resistances is to increase the effective length of the pipe. This length is added to the geometrical pipe length for friction calculations.

Internal surface absolute roughness — Average depth of surface defects on the internal surface of the pipe
`15e-6 m` (default) | positive scalar in units of length

Average depth of all surface defects on the internal surface of the pipe. The surface defects affect the pressure loss across the pipe in the turbulent flow regime.

Laminar flow upper Reynolds number limit — Reynolds number below which the flow is laminar
`2e+3` (default) | positive unitless scalar

Reynolds number above which the pipe flow begins to transition from laminar to turbulent. This value is the maximum Reynolds number corresponding to fully developed laminar flow.

Turbulent flow lower Reynolds number limit — Reynolds number above which the flow is turbulent
`4e+3` (default) | positive unitless scalar

Reynolds number below which the pipe flow begins to transition from turbulent to laminar. This value is the minimum Reynolds number corresponding to fully developed turbulent flow.

Shape factor for laminar flow viscous friction — Dimensionless factor used to capture the effect of geometry on viscous friction losses
`64` (default) | positive unitless scalar

Dimensionless factor used to capture the effects of cross-sectional geometry on the viscous friction losses incurred in the laminar flow regime. Typical values are 64 for a circular cross section, 57 for a square cross section, and 62 for a rectangular cross section with an aspect ratio of 2.

Heat Transfer

External environment heat transfer coefficient — Heat transfer coefficient between the environment and the pipe wall
`100 W/(m^2K)` (default) | positive scalar with units of power/(areatemperature)

Heat transfer coefficient for heat exchange between the environment (at port H) and the outer surface of the pipe wall. If this parameter is set to inf, then the thermal resistance between the environment and the wall is assumed to be zero. The pipe wall then has a uniform temperature equal to that associated with port H.

Wall thickness — Average thickness of the pipe wall material
`0 m` (default) | positive scalar with units of length

Average thickness of the pipe wall material. If this value is set to 0, then both thermal resistance due to conduction through the pipe wall and thermal storage due to the thermal mass of the pipe wall are assumed to be negligible.

Wall thermal conductivity — Thermal conductivity of the pipe wall material
`390 W/(mK)` (default) | positive scalar with units of power/(lengthtemperature)

Thermal conductivity of the pipe wall material. If this parameter is set to inf, then thermal resistance due to conduction through the pipe wall is assumed to be negligible.

Wall specific heat — Heat capacity per unit mass of pipe wall material
`390 J/kg/K` (default) | positive scalar with units of energy/(mass*temperature)

Heat capacity per unit mass of the pipe wall material. If this parameter is set to 0, then thermal storage due to the thermal mass of the pipe is assumed to be negligible.

Wall density — Mass density of the pipe wall material
`9e3 kg/m^3` (default) | positive scalar with units of mass/volume

Mass density of the pipe wall material. If this parameter is set to 0, then thermal storage due to the thermal mass of the pipe wall is assumed to be negligible.

Ratio of external fins surface area to no-fin surface area — Ratio of heat transfer surface area with external fins to that without
`0` (default) | positive unitless scalar

Ratio of the total heat transfer surface area of the fins on the external side of the pipe wall to that of the pipe wall without any fins. The presence of fins serves to enhance the convective heat transfer between the pipe wall and the environment.

External fin efficiency — Ratio of actual to ideal heat exchange rates with external fins
`0.5` (default) | positive unitless scalar

Ratio of the actual heat exchange rate between the external fins and the environment to its ideal value (if the fins were entirely held at the temperature of the pipe wall). This parameter is a function of fin geometry.

Ratio of internal fins surface area to no-fin surface area — Ratio of heat transfer surface area with internal fins to that without
`0` (default) | positive unitless scalar

Ratio of the total heat transfer surface area of the fins on the internal side of the pipe wall to that of the pipe wall without any fins. The presence of fins serves to enhance the convective heat transfer between the pipe wall and the fluid.

Internal fin efficiency — Ratio of actual to ideal heat exchange rates with internal fins
`0.5` (default) | positive unitless scalar

Ratio of the actual heat exchange rate between the internal fins and the environment to its ideal value (if the fins were entirely held at the temperature of the pipe wall). This parameter is a function of fin geometry.

Heat transfer coefficient model — Method of calculating heat transfer coefficient between fluid and wall
`Correlation for flow inside tubes` (default) | `Colburn equation`

Method of calculating the heat transfer coefficient between the fluid and the wall. The available settings are:

Colburn equation. Use this setting to calculate the heat transfer coefficient with user-defined variables a, b, and c. In the liquid and vapor zones, the heat transfer coefficient is based on the Colburn equation. In the liquid-vapor mixture zone, the heat transfer coefficient is based on the Cavallini-Zecchin equation.
Correlation for flow inside tubes. Use this setting to calculate the heat transfer coefficient for pipe flows. In the liquid and vapor zones, the heat transfer coefficient is calculated with the Gnielinski correlation. In the liquid-vapor mixture zone, the heat transfer coefficient is calculated with the Cavallini-Zecchin equation.

**Coefficients [a, b, c] for aRe^bPr^c in liquid zone** — Colburn equation coefficients in liquid zone
`[.023, .8, .33]` (default) | three-element vector of positive scalars

Three-element vector that contains the empirical coefficients of the Colburn equation. Each fluid zone has a distinct Nusselt number, which the block calculates by using the Colburn equation for each zone. The general form of the Colburn equation is:

$Nu = a {Re}^{b} {Pr}^{c} .$

Dependencies

To enable this parameter, set Heat transfer coefficient model to Colburn equation.

**Coefficients [a, b, c] for aRe^bPr^c in mixture zone** — Cavallini-Zecchin equation coefficients in mixture zone
`[.05, .8, .33]` (default) | three-element vector of positive scalars

Three-element vector that contains the empirical coefficients for the Cavallini-Zecchin equation. Each fluid zone has a distinct Nusselt number, which the block calculates in the mixture zone by using the Cavallini-Zecchin equation:

Dependencies

To enable this parameter, set Heat transfer coefficient model to Colburn equation.

**Coefficients [a, b, c] for aRe^bPr^c in vapor zone** — Colburn equation coefficients in vapor zone
`[.023, .8, .33]` (default) | three-element vector of positive scalars

$Nu = a {Re}^{b} {Pr}^{c} .$

Dependencies

To enable this parameter, set Heat transfer coefficient model to Colburn equation.

Nusselt number for laminar flow heat transfer — Ratio of convective to conductive heat exchange rates in the laminar flow regime
`3.66` (default)

Ratio of convective to conductive heat exchange rates in the laminar flow regime. This parameter is a function of pipe cross section geometry. Typical values are 3.66 for a circular cross section, 2.98 for a square cross section, and 3.39 for a rectangular cross section with an aspect ratio of 2.

Effects and Initial Conditions Tab

Initial fluid energy specification — Thermodynamic variable whose initial value to set
`Temperature` (default) | `Vapor quality` | `Vapor void fraction` | `Specific enthalpy` | `Specific internal energy`

Thermodynamic variable in terms of which to define the initial conditions of the component.

The value for Initial fluid energy specification parameter limits the available initial states for the two-phase fluid. When Initial fluid energy specification is:

Temperature — Specify an initial state that is a subcooled liquid or superheated vapor. You cannot specify a liquid-vapor mixture because the temperature is constant across the liquid-vapor mixture region.
Vapor quality — Specify an initial state that is a liquid-vapor mixture. You cannot specify a subcooled liquid or a superheated vapor because the liquid mass fraction is 0 and 1, respectively, across the whole region. Additionally, the block limits the pressure to below the critical pressure.
Vapor void fraction — Specify an initial state that is a liquid-vapor mixture. You cannot specify a subcooled liquid or a superheated vapor because the liquid mass fraction is 0 and 1, respectively, across the whole region. Additionally, the block limits the pressure to below the critical pressure.
Specific enthalpy — Specify the specific enthalpy of the fluid. The block does not limit the initial state.
Specific internal energy — Specify the specific internal energy of the fluid. The block does not limit the initial state.

Initial pressure — Absolute pressure at the start of simulation
`0.101325 MPa` (default) | scalar with units of pressure

Pressure in the pipe at the start of simulation, specified against absolute zero.

Initial temperature — Absolute temperature at the start of simulation
`293.15 K` (default) | scalar or two-element vector with units of temperature

Fluid temperature in the pipe at the start of simulation. This parameter can be a scalar or a 2-element vector. If it is a scalar, the initial temperature is assumed to be uniform throughout the pipe. If it is a vector, the initial temperature is assumed to vary linearly between the ports. The first vector element gives the initial temperature at the inlet and the second vector element that at the outlet.

Dependencies

This parameter is active when the Initial fluid energy specification option is set to Temperature.

Initial vapor quality — Mass fraction of vapor at the start of simulation
`0.5` (default) | unitless scalar between 0 and 1

Vapor quality, or mass fraction of vapor, in the pipe at the start of simulation. This parameter can be a scalar or a 2-element vector. If it is a scalar, the initial vapor quality is assumed to be uniform throughout the pipe. If it is a vector, the initial vapor quality is assumed to vary linearly between the ports. The first vector element gives the initial vapor quality at the inlet and the second vector element that at the outlet.

Dependencies

This parameter is active when the Initial fluid energy specification option is set to Vapor quality.

Initial vapor void fraction — Volume fraction of vapor at the start of simulation
`0.5` (default) | unitless scalar between 0 and 1

Vapor void fraction, or vapor volume fraction, in the pipe at the start of simulation. This parameter can be a scalar or a 2-element vector. If it is a scalar, the initial vapor void fraction is assumed to be uniform throughout the pipe. If it is a vector, the initial vapor void fraction is assumed to vary linearly between the ports. The first vector element gives the initial vapor void fraction at the inlet and the second vector element that at the outlet..

Dependencies

This parameter is active when the Initial fluid energy specification option is set to Vapor void fraction.

Initial specific enthalpy — Specific enthalpy at the start of simulation
`1500 kJ/kg` (default) | scalar with units of energy/mass

Specific enthalpy of the fluid in the pipe at the start of simulation. This parameter can be a scalar or a 2-element vector. If it is a scalar, the initial specific enthalpy is assumed to be uniform throughout the pipe. If it is a vector, the initial specific enthalpy is assumed to vary linearly between the ports. The first vector element gives the initial specific enthalpy at the inlet and the second vector element that at the outlet.

Dependencies

This parameter is active when the Initial fluid energy specification option is set to Specific enthalpy.

Initial specific internal energy — Specific internal energy at the start of simulation
`1500 kJ/kg` (default) | scalar with units of energy/mass

Specific internal energy of the fluid in the pipe at the start of simulation. This parameter can be a scalar or a 2-element vector. If it is a scalar, the initial specific internal energy is assumed to be uniform throughout the pipe. If it is a vector, the initial specific internal energy is assumed to vary linearly between the ports. The first vector element gives the initial specific internal energy at the inlet and the second vector element that at the outlet.

Dependencies

This parameter is active when the Initial fluid energy specification option is set to Specific internal energy.

References

[1] White, F.M., Fluid Mechanics, 7^th Ed, Section 6.8. McGraw-Hill, 2011.

[2] Çengel, Y.A., Heat and Mass Transfer—A Practical Approach, 3^rd Ed, Section 8.5. McGraw-Hill, 2007.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2018b

expand all

R2023b: Model elevation gain and hydrostatic pressure

The 3-Zone Pipe (2P) block now allows you to model elevation gain and hydrostatic pressure. Use the new Elevation gain from port A to port B and Gravitational acceleration parameters to control these effects.

R2022b: Parameterize using a new heat transfer coefficient model

The 3-Zone Pipe (2P) block now allows you to more explicitly control the heat transfer process. You can set the new Heat transfer coefficient model parameter to:

Correlation for flow inside tubes — The Gnielinski correlation predicts heat transfer of turbulent flows in subcooled liquid or superheated vapor zones, and the Cavallini-Zecchin correlation predicts the heat transfer of turbulent flows in the liquid-vapor mixture zone. The block predefines the coefficients a, b, and c. This is how the block operates in previous releases.
Colburn equation — The block allows you to define the coefficients a, b, and c for each flow zone by using the Coefficients [a, b, c] for a*Re^b*Pr^c in liquid zone, Coefficients [a, b, c] for a*Re^b*Pr^c in mixture zone, and Coefficients [a, b, c] for a*Re^b*Pr^c in vapor zone parameters. You specify these parameters as three-element vectors where the first element is a, the second is b, and the third is c.

3-Zone Pipe (2P)

Description

Heat Transfer Between the Fluid and the Wall

Heat Transfer Between the Wall and the Environment

Momentum Balance

Mass Balance

Energy Balance

Assumptions and Limitations

Examples

Pipe Fluid Vaporization and Condensation

Ports

Output

Z — Zone length fractions physical signal

Conserving

A — Pipe opening two-phase fluid

B — Pipe opening two-phase fluid

H — Pipe wall thermal

Parameters

Geometry

Pipe length — Distance between the ports of the pipe 5 m (default) | positive scalar with units of length

Cross-sectional area — Internal area normal to the direction of the flow 0.01 m^2 (default) | positive scalar with units of area

Hydraulic diameter — Diameter of a cylindrical pipe with the given cross-sectional area 0.1 m (default) | positive scalar in units of length

Elevation gain from port A to port B — Constant pipe elevation differential 0 m (default) | scalar

Gravitational acceleration — Gravitational acceleration 9.81 m/s^2 (default) | scalar

Viscous Friction

Aggregate equivalent length of local resistances — Minor pressure loss in the pipe expressed as a length 1 m (default) | positive scalar in units of length

Internal surface absolute roughness — Average depth of surface defects on the internal surface of the pipe 15e-6 m (default) | positive scalar in units of length

Laminar flow upper Reynolds number limit — Reynolds number below which the flow is laminar 2e+3 (default) | positive unitless scalar

Turbulent flow lower Reynolds number limit — Reynolds number above which the flow is turbulent 4e+3 (default) | positive unitless scalar

Shape factor for laminar flow viscous friction — Dimensionless factor used to capture the effect of geometry on viscous friction losses 64 (default) | positive unitless scalar

Heat Transfer

External environment heat transfer coefficient — Heat transfer coefficient between the environment and the pipe wall 100 W/(m^2*K) (default) | positive scalar with units of power/(area*temperature)

Wall thickness — Average thickness of the pipe wall material 0 m (default) | positive scalar with units of length

Wall thermal conductivity — Thermal conductivity of the pipe wall material 390 W/(m*K) (default) | positive scalar with units of power/(length*temperature)

Wall specific heat — Heat capacity per unit mass of pipe wall material 390 J/kg/K (default) | positive scalar with units of energy/(mass*temperature)

Wall density — Mass density of the pipe wall material 9e3 kg/m^3 (default) | positive scalar with units of mass/volume

Ratio of external fins surface area to no-fin surface area — Ratio of heat transfer surface area with external fins to that without 0 (default) | positive unitless scalar

External fin efficiency — Ratio of actual to ideal heat exchange rates with external fins 0.5 (default) | positive unitless scalar

Ratio of internal fins surface area to no-fin surface area — Ratio of heat transfer surface area with internal fins to that without 0 (default) | positive unitless scalar

Internal fin efficiency — Ratio of actual to ideal heat exchange rates with internal fins 0.5 (default) | positive unitless scalar

Heat transfer coefficient model — Method of calculating heat transfer coefficient between fluid and wall Correlation for flow inside tubes (default) | Colburn equation

Coefficients [a, b, c] for a*Re^b*Pr^c in liquid zone — Colburn equation coefficients in liquid zone [.023, .8, .33] (default) | three-element vector of positive scalars

Dependencies

Coefficients [a, b, c] for a*Re^b*Pr^c in mixture zone — Cavallini-Zecchin equation coefficients in mixture zone [.05, .8, .33] (default) | three-element vector of positive scalars

Dependencies

Coefficients [a, b, c] for a*Re^b*Pr^c in vapor zone — Colburn equation coefficients in vapor zone [.023, .8, .33] (default) | three-element vector of positive scalars

Dependencies

Nusselt number for laminar flow heat transfer — Ratio of convective to conductive heat exchange rates in the laminar flow regime 3.66 (default)

Effects and Initial Conditions Tab

Initial fluid energy specification — Thermodynamic variable whose initial value to set Temperature (default) | Vapor quality | Vapor void fraction | Specific enthalpy | Specific internal energy

Initial pressure — Absolute pressure at the start of simulation 0.101325 MPa (default) | scalar with units of pressure

Initial temperature — Absolute temperature at the start of simulation 293.15 K (default) | scalar or two-element vector with units of temperature

Dependencies

Initial vapor quality — Mass fraction of vapor at the start of simulation 0.5 (default) | unitless scalar between 0 and 1

Dependencies

Initial vapor void fraction — Volume fraction of vapor at the start of simulation 0.5 (default) | unitless scalar between 0 and 1

Dependencies

Initial specific enthalpy — Specific enthalpy at the start of simulation 1500 kJ/kg (default) | scalar with units of energy/mass

Dependencies

Initial specific internal energy — Specific internal energy at the start of simulation 1500 kJ/kg (default) | scalar with units of energy/mass

Dependencies

References

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using Simulink® Coder™.

Version History

R2023b: Model elevation gain and hydrostatic pressure

R2022b: Parameterize using a new heat transfer coefficient model

See Also

Z — Zone length fractions
physical signal

A — Pipe opening
two-phase fluid

B — Pipe opening
two-phase fluid

H — Pipe wall
thermal

Pipe length — Distance between the ports of the pipe
`5 m` (default) | positive scalar with units of length

Cross-sectional area — Internal area normal to the direction of the flow
`0.01 m^2` (default) | positive scalar with units of area

Hydraulic diameter — Diameter of a cylindrical pipe with the given cross-sectional area
`0.1 m` (default) | positive scalar in units of length

Elevation gain from port A to port B — Constant pipe elevation differential
`0 m` (default) | scalar

Gravitational acceleration — Gravitational acceleration
`9.81 m/s^2` (default) | scalar

Aggregate equivalent length of local resistances — Minor pressure loss in the pipe expressed as a length
`1 m` (default) | positive scalar in units of length

Internal surface absolute roughness — Average depth of surface defects on the internal surface of the pipe
`15e-6 m` (default) | positive scalar in units of length

Laminar flow upper Reynolds number limit — Reynolds number below which the flow is laminar
`2e+3` (default) | positive unitless scalar

Turbulent flow lower Reynolds number limit — Reynolds number above which the flow is turbulent
`4e+3` (default) | positive unitless scalar

Shape factor for laminar flow viscous friction — Dimensionless factor used to capture the effect of geometry on viscous friction losses
`64` (default) | positive unitless scalar

External environment heat transfer coefficient — Heat transfer coefficient between the environment and the pipe wall
`100 W/(m^2K)` (default) | positive scalar with units of power/(areatemperature)

Wall thickness — Average thickness of the pipe wall material
`0 m` (default) | positive scalar with units of length

Wall thermal conductivity — Thermal conductivity of the pipe wall material
`390 W/(mK)` (default) | positive scalar with units of power/(lengthtemperature)

Wall specific heat — Heat capacity per unit mass of pipe wall material
`390 J/kg/K` (default) | positive scalar with units of energy/(mass*temperature)

Wall density — Mass density of the pipe wall material
`9e3 kg/m^3` (default) | positive scalar with units of mass/volume

Ratio of external fins surface area to no-fin surface area — Ratio of heat transfer surface area with external fins to that without
`0` (default) | positive unitless scalar

External fin efficiency — Ratio of actual to ideal heat exchange rates with external fins
`0.5` (default) | positive unitless scalar

Ratio of internal fins surface area to no-fin surface area — Ratio of heat transfer surface area with internal fins to that without
`0` (default) | positive unitless scalar

Internal fin efficiency — Ratio of actual to ideal heat exchange rates with internal fins
`0.5` (default) | positive unitless scalar

Heat transfer coefficient model — Method of calculating heat transfer coefficient between fluid and wall
`Correlation for flow inside tubes` (default) | `Colburn equation`

**Coefficients [a, b, c] for aRe^bPr^c in liquid zone** — Colburn equation coefficients in liquid zone
`[.023, .8, .33]` (default) | three-element vector of positive scalars

**Coefficients [a, b, c] for aRe^bPr^c in mixture zone** — Cavallini-Zecchin equation coefficients in mixture zone
`[.05, .8, .33]` (default) | three-element vector of positive scalars

**Coefficients [a, b, c] for aRe^bPr^c in vapor zone** — Colburn equation coefficients in vapor zone
`[.023, .8, .33]` (default) | three-element vector of positive scalars

Nusselt number for laminar flow heat transfer — Ratio of convective to conductive heat exchange rates in the laminar flow regime
`3.66` (default)

Initial fluid energy specification — Thermodynamic variable whose initial value to set
`Temperature` (default) | `Vapor quality` | `Vapor void fraction` | `Specific enthalpy` | `Specific internal energy`

Initial pressure — Absolute pressure at the start of simulation
`0.101325 MPa` (default) | scalar with units of pressure

Initial temperature — Absolute temperature at the start of simulation
`293.15 K` (default) | scalar or two-element vector with units of temperature

Initial vapor quality — Mass fraction of vapor at the start of simulation
`0.5` (default) | unitless scalar between 0 and 1

Initial vapor void fraction — Volume fraction of vapor at the start of simulation
`0.5` (default) | unitless scalar between 0 and 1

Initial specific enthalpy — Specific enthalpy at the start of simulation
`1500 kJ/kg` (default) | scalar with units of energy/mass

Initial specific internal energy — Specific internal energy at the start of simulation
`1500 kJ/kg` (default) | scalar with units of energy/mass

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.