Check Valve

(To be removed) Hydraulic valve that allows flow in one direction only

The Hydraulics (Isothermal) library will be removed in a future release. Use the Isothermal Liquid library instead. (since R2020a)

For more information on updating your models, see Upgrading Hydraulic Models to Use Isothermal Liquid Blocks.

Libraries:
Simscape / Fluids / Hydraulics (Isothermal) / Valves / Directional Valves

Description

The Check Valve block represents a hydraulic check valve as a data-sheet-based model. The check valve permits flow in one direction and blocks it in the opposite direction. This figure shows the typical dependency between the valve passage area A and the pressure differential across the valve $Δ p = p_{A} - p_{B}$ .

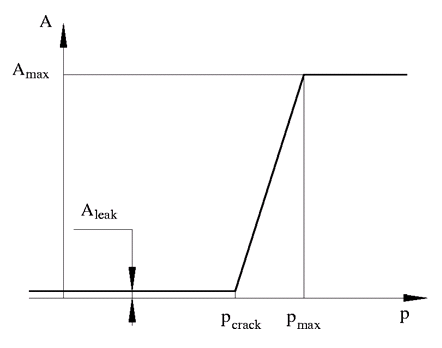
The valve remains closed when the pressure differential across the valve is lower than the valve cracking pressure. When cracking pressure is reached, the valve control member, such as a spool or poppet, is forced off its seat, thus creating a passage between the inlet and outlet. If the flow rate is high enough and pressure continues to rise, the area increases until the control member reaches its maximum displacement. At this moment, the valve passage area is at its maximum. The catalogs and manufacturer data sheets generally provide the valve maximum area and the cracking and maximum pressures.

The leakage area is also required to characterize the valve. The Leakage area parameter accounts for possible leakage and maintains the numerical integrity of the circuit, by preventing a portion of the system from getting isolated after the valve is completely closed. Because isolated parts of the system could affect computational efficiency or cause failure of computation, the parameter value must be greater than zero.

By default, the block does not include the valve opening dynamics, and the valve sets its opening area directly as a function of pressure:

$A = A (p) .$

Adding valve opening dynamics provides continuous behavior that is more physically realistic, and is helpful in situations with rapid valve opening and closing. The pressure-dependent orifice passage area A(p) in the block equations then becomes the steady-state area, and the instantaneous orifice passage area in the flow equation is:

$A (t = 0) = A_{i n i t}$

$\frac{d A}{d t} = \frac{A (p) - A}{τ}$

For both settings of Opening dynamics, the flow rate through the valve is:

$q = C_{D} \cdot A \sqrt{\frac{2}{ρ}} \cdot \frac{p}{{(p^{2} + p_{c r}^{2})}^{1 / 4}}$

$A (p) = {\begin{array}{l} A_{l e a k} & for p < = p_{c r a c k} \\ A_{l e a k} + k \cdot (p - p_{c r a c k}) & for p_{c r a c k} < p < p_{\max} \\ A_{\max} & for p > = p_{\max} \end{array}$

$k = \frac{A_{\max} - A_{l e a k}}{p_{\max} - p_{c r a c k}}$

$Δ p = p_{A} - p_{B},$

$D_{H} = \sqrt{\frac{4 A}{π}}$

When Laminar Transition specification is Reynolds number,

$p_{c r} = \frac{ρ}{2} {(\frac{{Re}_{c r} \cdot ν}{C_{D} \cdot D_{H}})}^{2}$

When Laminar Transition specification is Pressure ratio,

$p_{c r} = (\frac{p_{A} + p_{B}}{2} + p_{a t m}) (1 - B_{l a m})$

where:

q	Flow rate
p	Pressure differential
p_A, p_B	Gauge pressures at the block terminals
C_D	Flow discharge coefficient
A	Instantaneous orifice passage area
A(p)	Pressure-dependent orifice passage area
A_init	Initial open area of the valve
A_max	Fully open valve passage area
A_leak	Closed valve leakage area
p_crack	Valve cracking pressure
p_max	Pressure needed to fully open the valve
p_cr	Minimum pressure for turbulent flow
Re_cr	Critical Reynolds number
D_H	Instantaneous orifice hydraulic diameter
ρ	Fluid density
ν	Fluid kinematic viscosity
τ	Time constant for the first order response of the valve opening
B_lam	Value of the Laminar flow pressure ratio parameter
t	Time

The block positive direction is from port A to port B. This means that the flow rate is positive if it flows from A to B, and the pressure differential is $Δ p = p_{A} - p_{B}$ .

Variables

To set the priority and initial target values for the block variables prior to simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.

Nominal values provide a way to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. Nominal values can come from different sources, one of which is the Nominal Values section in the block dialog box or Property Inspector. For more information, see Modify Nominal Values for a Block Variable.

Assumptions and Limitations

The valve opening is linearly proportional to the pressure differential.
The block does not consider loading on the valve, such as inertia, friction, spring, and so on.

Examples

Hydraulic Flow Rectifier Circuit

A flow rectifier circuit, which consists of four check valves and a flow control valve. It is used to control flow rate flowing in both directions with only one flow control valve. Similar to a Graetz circuit implemented with diodes, the check valves are arranged in such a way that flow always passes through the flow control valve in the same direction. Two other check valves, Flow BA Check Valve and Flow AB Check Valve, are used to select an orifice depending on the flow direction.

Open Model

Ports

Conserving

expand all

A — Valve inlet
hydraulic

Hydraulic conserving port associated with the valve inlet.

B — Valve outlet
hydraulic

Hydraulic conserving port associated with the valve outlet.

Parameters

expand all

Maximum passage area — Valve passage maximum cross-sectional area
`1e-4 m^2` (default) | positive scalar

Maximum cross-sectional area of the valve passage.

Cracking pressure — Pressure level at which orifice of valve starts to open
`0.3e5 Pa` (default) | positive scalar

Pressure level at which the orifice of the valve starts to open.

Maximum opening pressure — Pressure differential across valve needed to fully open valve
`1.2e5 Pa` (default) | positive scalar

Pressure differential across the valve needed to fully open the valve. This value must be higher than the cracking pressure.

Flow discharge coefficient — Valve capacity characterization
`0.7` (default) | positive scalar

Semi-empirical parameter for the valve capacity characterization. This value depends on the geometrical properties of the orifice. Manufacturer data sheets and textbooks typically provide this value.

Leakage area — Total area of possible leaks in the completely closed valve
`1e-12 m^2` (default) | positive scalar

Total area of possible leaks in the completely closed valve. This parameter maintains the numerical integrity of the circuit by preventing a portion of the system from being isolated when the valve is completely closed.

Laminar transition specification — How block transitions between laminar and turbulent regimes
`Pressure ratio` (default) | `Reynolds number`

How the block transitions between the laminar and turbulent regimes:

Pressure ratio — The transition from laminar to turbulent regime is smooth and depends on the value of the Laminar flow pressure ratio parameter. This method provides better simulation robustness.
Reynolds number — The transition from laminar to turbulent regime takes place when the Reynolds number reaches the value specified by the Critical Reynolds number parameter.

Laminar flow pressure ratio — Pressure ratio at which flow transitions between laminar and turbulent regimes
`0.999` (default) | scalar between 0 and 1

Pressure ratio at which the flow transitions between laminar and turbulent regimes.

Dependencies

To enable this parameter, set Laminar transition specification to Pressure ratio.

Critical Reynolds number — Maximum Reynolds number for laminar flow
`12` (default) | positive scalar

Maximum Reynolds number for laminar flow. This value depends on the orifice geometrical profile. You can find recommendations for this value in hydraulics textbooks. The default value, 12, corresponds to a round orifice in thin material with sharp edges.

Dependencies

To enable this parameter, set Laminar transition specification to Reynolds number.

Opening dynamics — Whether to include valve opening dynamics
`Do not include valve opening dynamics` (default) | `Include valve opening dynamics`

Whether to include the valve opening dynamics. Select one of the following options:

Do not include valve opening dynamics — The valve sets its orifice passage area directly as a function of pressure. If the area changes instantaneously, so does the flow equation.
Include valve opening dynamics — This setting provides continuous behavior that is more physically realistic by adding a first-order lag when the valve opens and closes. Use this option in hydraulic simulations with the local solver for real-time simulation. This option is also helpful if you are interested in valve opening dynamics in variable step simulations.

Opening time constant — Time constant for first-order response of valve opening
`0.1 s` (default) | positive scalar

Time constant for the first-order response of the valve opening.

Dependencies

To enable this parameter, set Opening dynamics to Include valve opening dynamics.

Initial area — Initial opening area of valve
`1e-12 m^2` (default) | positive scalar

Initial opening area of the valve. This value must be greater than the Leakage area parameter and less than the Maximum passage area parameter.

Dependencies

To enable this parameter, set Opening dynamics to Include valve opening dynamics.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2006a

collapse all

R2023a: To be removed

The Hydraulics (Isothermal) library will be removed in a future release. Use the Isothermal Liquid library instead.

For more information on updating your models, see Upgrading Hydraulic Models to Use Isothermal Liquid Blocks.

Check Valve

Description

Variables

Assumptions and Limitations

Examples

Hydraulic Flow Rectifier Circuit

Ports

Conserving

A — Valve inlet hydraulic

B — Valve outlet hydraulic

Parameters

Maximum passage area — Valve passage maximum cross-sectional area 1e-4 m^2 (default) | positive scalar

Cracking pressure — Pressure level at which orifice of valve starts to open 0.3e5 Pa (default) | positive scalar

Maximum opening pressure — Pressure differential across valve needed to fully open valve 1.2e5 Pa (default) | positive scalar

Flow discharge coefficient — Valve capacity characterization 0.7 (default) | positive scalar

Leakage area — Total area of possible leaks in the completely closed valve 1e-12 m^2 (default) | positive scalar

Laminar transition specification — How block transitions between laminar and turbulent regimes Pressure ratio (default) | Reynolds number

Laminar flow pressure ratio — Pressure ratio at which flow transitions between laminar and turbulent regimes 0.999 (default) | scalar between 0 and 1

Dependencies

Critical Reynolds number — Maximum Reynolds number for laminar flow 12 (default) | positive scalar

Dependencies

Opening dynamics — Whether to include valve opening dynamics Do not include valve opening dynamics (default) | Include valve opening dynamics

Opening time constant — Time constant for first-order response of valve opening 0.1 s (default) | positive scalar

Dependencies

Initial area — Initial opening area of valve 1e-12 m^2 (default) | positive scalar

Dependencies

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using Simulink® Coder™.

Version History

R2023a: To be removed

See Also

A — Valve inlet
hydraulic

B — Valve outlet
hydraulic

Maximum passage area — Valve passage maximum cross-sectional area
`1e-4 m^2` (default) | positive scalar

Cracking pressure — Pressure level at which orifice of valve starts to open
`0.3e5 Pa` (default) | positive scalar

Maximum opening pressure — Pressure differential across valve needed to fully open valve
`1.2e5 Pa` (default) | positive scalar

Flow discharge coefficient — Valve capacity characterization
`0.7` (default) | positive scalar

Leakage area — Total area of possible leaks in the completely closed valve
`1e-12 m^2` (default) | positive scalar

Laminar transition specification — How block transitions between laminar and turbulent regimes
`Pressure ratio` (default) | `Reynolds number`

Laminar flow pressure ratio — Pressure ratio at which flow transitions between laminar and turbulent regimes
`0.999` (default) | scalar between 0 and 1

Critical Reynolds number — Maximum Reynolds number for laminar flow
`12` (default) | positive scalar

Opening dynamics — Whether to include valve opening dynamics
`Do not include valve opening dynamics` (default) | `Include valve opening dynamics`

Opening time constant — Time constant for first-order response of valve opening
`0.1 s` (default) | positive scalar

Initial area — Initial opening area of valve
`1e-12 m^2` (default) | positive scalar

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.