Pilot-Operated Check Valve

(To be removed) Hydraulic check valve that allows flow in one direction, but can be disabled by pilot pressure

The Hydraulics (Isothermal) library will be removed in a future release. Use the Isothermal Liquid library instead. (since R2020a)

For more information on updating your models, see Upgrading Hydraulic Models to Use Isothermal Liquid Blocks.

Libraries:
Simscape / Fluids / Hydraulics (Isothermal) / Valves / Directional Valves

Description

The Pilot-Operated Check Valve block represents a hydraulic pilot-operated check valve as a data-sheet-based model. The purpose of the check valve is to permit flow in one direction and block it in the opposite direction, as shown in the following figure.

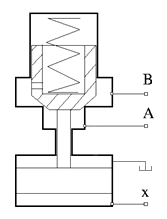
Unlike a conventional check valve, the pilot-operated check valve can be opened by inlet pressure p_A, pilot pressure p_X, or both. The force acting on the poppet is based on the expression

$F = p_{A} \cdot A_{A} + p_{X} \cdot A_{X} - p_{B} \cdot A_{B}$

where

p_A, p_B	Gauge pressures at the valve terminals
p_X	Pressure—gauge or differential—at the pilot terminal
A_A	Area of the spool in the A chamber
A_B	Area of the spool in the B chamber
A_X	Area of the pilot chamber

The force equation is commonly expressed in the slightly modified form

$p_{e} = p_{A} + p_{X} \cdot k_{p} - p_{B}$

where k_p = A_X / A_A is usually referred to as pilot ratio and p_e is the effective pressure differential across the control member. The valve remains closed while this pressure differential across the valve is lower than the valve cracking pressure. When cracking pressure is reached, the valve control member is forced off its seat, thus creating a passage between the inlet and outlet. If the flow rate is high enough and pressure continues to rise, the area is further increased until the control member reaches its maximum. At this moment, the valve passage area is at its maximum. The valve maximum area and the cracking and maximum pressures are generally provided in the catalogs and are the three key parameters of the block.

The pilot pressure can be a differential value relative to the inlet (port A) or a gauge value (relative to the environment). You can select an appropriate setting—Pressure differential (pX - pA) or Pressure at port X—using the Pressure control specification dropdown list. If Pressure at port X is selected:

$p_{X} = p_{X,Abs} - p_{Atm},$

where the subscript Atm denotes atmospheric pressure. The subscript X,Abs denotes the absolute value at the pilot port. If Pressure differential (pX - pA) is selected:

$p_{X} = p_{X,Abs} - p_{A,Abs}$

where the subscript A,Abs similarly denotes the absolute value at the inlet of the valve (port A). The pilot pressure differential is constrained to be greater than or equal to zero—if its calculated value should be negative, zero is assumed in the control pressure calculation.

In addition to the maximum area, the leakage area is also required to characterize the valve. The main purpose of the parameter is not to account for possible leakage, even though this is also important, but to maintain numerical integrity of the circuit by preventing a portion of the system from getting isolated after the valve is completely closed. An isolated or “hanging” part of the system could affect computational efficiency and even cause failure of computation. Therefore, the parameter value must be greater than zero.

By default, the block does not include valve opening dynamics, and the valve sets its opening area directly as a function of pressure:

$A = A (p)$

Adding valve opening dynamics provides continuous behavior that is more physically realistic, and is particularly helpful in situations with rapid valve opening and closing. The pressure-dependent orifice passage area A(p) in the block equations then becomes the steady-state area, and the instantaneous orifice passage area in the flow equation is determined as follows:

$A (t = 0) = A_{i n i t}$

$\frac{d A}{d t} = \frac{A (p) - A}{τ}$

In either case, the flow rate through the valve is determined according to the following equations:

$q = C_{D} \cdot A \sqrt{\frac{2}{ρ}} \cdot \frac{p}{{(p^{2} + p_{c r}^{2})}^{1 / 4}}$

$p_{e} = p_{A} + p_{X} \cdot k_{p} - p_{B}$

$A (p) = {\begin{array}{l} A_{l e a k} & for p_{e} < = p_{c r a c k} \\ A_{l e a k} + k \cdot (p_{e} - p_{c r a c k}) & for p_{c r a c k} < p_{e} < p_{\max} \\ A_{\max} & for p_{e} > = p_{\max} \end{array}$

$k = \frac{A_{\max} - A_{l e a k}}{p_{\max} - p_{c r a c k}}$

$Δ p = p_{A} - p_{B},$

$p_{c r} = \frac{ρ}{2} {(\frac{{Re}_{c r} \cdot ν}{C_{D} \cdot D_{H}})}^{2}$

$D_{H} = \sqrt{\frac{4 A}{π}}$

where

q	Flow rate through the valve
p	Pressure differential across the valve
p_e	Equivalent pressure differential across the control member
`p_A,p_B`	Gauge pressures at the valve terminals
p_X	Gauge pressure at the pilot terminal
k_p	Pilot ratio, k_p = A_X / A_A
k	Valve gain coefficient
C_D	Flow discharge coefficient
A	Instantaneous orifice passage area
A(p)	Pressure-dependent orifice passage area
A_init	Initial open area of the valve
`A_max`	Fully open valve passage area
`A_leak`	Closed valve leakage area
p_crack	Valve cracking pressure
p_max	Pressure needed to fully open the valve
p_cr	Minimum pressure for turbulent flow
Re_cr	Critical Reynolds number
D_H	Instantaneous orifice hydraulic diameter
ρ	Fluid density
ν	Fluid kinematic viscosity
τ	Time constant for the first order response of the valve opening
t	Time

The block positive direction is from port A to port B. This means that the flow rate is positive if it flows from A to B, and the pressure differential is determined as $Δ p = p_{A} - p_{B},$ .

Examples

Pilot-Operated Check Valve Test Rig

A test circuit built to check the characteristics of a pilot-operated check valve. The valve is loaded with three ideal pressure sources, two of which create pressure differential across the main flow line, while the third applies pressure to the pilot inlet X. The pilot pressure allows flow through the valve even if the main pressure differential is negative.

Open Model

Assumptions and Limitations

Valve opening is linearly proportional to the effective pressure differential.
No loading on the valve, such as inertia, friction, spring, and so on, is considered.
No flow consumption is associated with the pilot chamber.

Ports

Conserving

expand all

A — Valve inlet
hydraulic

Hydraulic conserving port associated with the valve inlet.

B — Valve outlet
hydraulic

Hydraulic conserving port associated with the valve outlet.

X — Valve pilot terminal
hydraulic

Hydraulic conserving port associated with the valve pilot terminal.

Parameters

expand all

Pressure control specification — Choice of pressure measurement to use as pilot control signal
`Pressure differential (pX - pA)` (default) | `Pressure at port X`

Choice of pressure measurement to use as pilot control signal:

Pressure differential (pX - pA) — The effective pressure differential is a function of the pressure drop from the pilot port (X) to the inlet (A).
Pressure at port X — The effective pressure differential is a function of the gauge pressure at the inlet.

The block uses the chosen measurement to calculate the effective pressure differential across the valve. See the block description for the calculations.

Cracking pressure — Pressure level at which the orifice of the valve starts to open
`3e4 Pa` (default) | positive scalar

Pressure level at which the orifice of the valve starts to open.

Maximum opening pressure — Pressure differential across the valve needed to fully open the valve
`1.2e5 Pa` (default) | positive scalar

Pressure differential across the valve needed to fully open the valve. Its value must be higher than the cracking pressure.

Pilot ratio — Ratio between effective area in the pilot chamber to the effective area in the inlet chamber
`5` (default) | positive scalar

Ratio between effective area in the pilot chamber to the effective area in the inlet chamber.

Maximum passage area — Valve passage maximum cross-sectional area
`1e-4 m^2` (default) | positive scalar

Valve passage maximum cross-sectional area.

Leakage area — Helps maintain numerical integrity of the circuit
`1e-12 m^2` (default) | positive scalar

The total area of possible leaks in the completely closed valve. The main purpose of the parameter is to maintain numerical integrity of the circuit by preventing a portion of the system from getting isolated after the valve is completely closed. The parameter value must be greater than 0.

Laminar transition specification — Select how block transitions between the laminar and turbulent regimes
`Pressure ratio` (default) | `Reynolds number`

Select how the block transitions between the laminar and turbulent regimes:

Pressure ratio — The transition from laminar to turbulent regime is smooth and depends on the value of the Laminar flow pressure ratio parameter. This method provides better simulation robustness.
Reynolds number — The transition from laminar to turbulent regime is assumed to take place when the Reynolds number reaches the value specified by the Critical Reynolds number parameter.

Laminar flow pressure ratio — Pressure ratio at which the flow transitions between laminar and turbulent regimes
`0.999` (default) | positive scalar in the range of [0,1]

Pressure ratio at which the flow transitions between laminar and turbulent regimes.

Dependencies

This parameter is visible only if the Laminar transition specification parameter is set to Pressure ratio.

Critical Reynolds number — Maximum Reynolds number for laminar flow
`12` (default) | positive scalar

The maximum Reynolds number for laminar flow. The value of the parameter depends on the orifice geometrical profile. You can find recommendations on the parameter value in hydraulics textbooks. The default value is 12, which corresponds to a round orifice in thin material with sharp edges.

Dependencies

This parameter is visible only if the Laminar transition specification parameter is set to Reynolds number.

Flow discharge coefficient — Semi-empirical parameter for valve capacity characterization
`0.7` (default) | positive scalar

Semi-empirical parameter for valve capacity characterization. Its value depends on the geometrical properties of the orifice, and usually is provided in textbooks or manufacturer data sheets.

Opening dynamics — Specify whether to include valve opening dynamics in simulation
`Do not include valve opening dynamics` (default) | `Include valve opening dynamics`

Select one of the following options:

Do not include valve opening dynamics — The valve sets its orifice passage area directly as a function of pressure. If the area changes instantaneously, so does the flow equation.
Include valve opening dynamics — Provide continuous behavior that is more physically realistic, by adding a first-order lag during valve opening and closing. Use this option in hydraulic simulations with the local solver for real-time simulation. This option is also helpful if you are interested in valve opening dynamics in variable step simulations.

Opening time constant — Time constant for the first order response of the valve opening
`0.1 s` (default) | positive scalar

The time constant for the first order response of the valve opening.

Dependencies

To enable this parameter, set Opening dynamics to Include valve opening dynamics.

Initial area — Initial opening area of the valve
`1e-12 m^2` (default) | positive scalar

The initial opening area of the valve.

Dependencies

To enable this parameter, set Opening dynamics to Include valve opening dynamics.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2006a

collapse all

R2023a: To be removed

The Hydraulics (Isothermal) library will be removed in a future release. Use the Isothermal Liquid library instead.

For more information on updating your models, see Upgrading Hydraulic Models to Use Isothermal Liquid Blocks.

Pilot-Operated Check Valve

Description

Examples

Pilot-Operated Check Valve Test Rig

Assumptions and Limitations

Ports

Conserving

A — Valve inlet hydraulic

B — Valve outlet hydraulic

X — Valve pilot terminal hydraulic

Parameters

Pressure control specification — Choice of pressure measurement to use as pilot control signal Pressure differential (pX - pA) (default) | Pressure at port X

Cracking pressure — Pressure level at which the orifice of the valve starts to open 3e4 Pa (default) | positive scalar

Maximum opening pressure — Pressure differential across the valve needed to fully open the valve 1.2e5 Pa (default) | positive scalar

Pilot ratio — Ratio between effective area in the pilot chamber to the effective area in the inlet chamber 5 (default) | positive scalar

Maximum passage area — Valve passage maximum cross-sectional area 1e-4 m^2 (default) | positive scalar

Leakage area — Helps maintain numerical integrity of the circuit 1e-12 m^2 (default) | positive scalar

Laminar transition specification — Select how block transitions between the laminar and turbulent regimes Pressure ratio (default) | Reynolds number

Laminar flow pressure ratio — Pressure ratio at which the flow transitions between laminar and turbulent regimes 0.999 (default) | positive scalar in the range of [0,1]

Dependencies

Critical Reynolds number — Maximum Reynolds number for laminar flow 12 (default) | positive scalar

Dependencies

Flow discharge coefficient — Semi-empirical parameter for valve capacity characterization 0.7 (default) | positive scalar

Opening dynamics — Specify whether to include valve opening dynamics in simulation Do not include valve opening dynamics (default) | Include valve opening dynamics

Opening time constant — Time constant for the first order response of the valve opening 0.1 s (default) | positive scalar

Dependencies

Initial area — Initial opening area of the valve 1e-12 m^2 (default) | positive scalar

Dependencies

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using Simulink® Coder™.

Version History

R2023a: To be removed

See Also

A — Valve inlet
hydraulic

B — Valve outlet
hydraulic

X — Valve pilot terminal
hydraulic

Pressure control specification — Choice of pressure measurement to use as pilot control signal
`Pressure differential (pX - pA)` (default) | `Pressure at port X`

Cracking pressure — Pressure level at which the orifice of the valve starts to open
`3e4 Pa` (default) | positive scalar

Maximum opening pressure — Pressure differential across the valve needed to fully open the valve
`1.2e5 Pa` (default) | positive scalar

Pilot ratio — Ratio between effective area in the pilot chamber to the effective area in the inlet chamber
`5` (default) | positive scalar

Maximum passage area — Valve passage maximum cross-sectional area
`1e-4 m^2` (default) | positive scalar

Leakage area — Helps maintain numerical integrity of the circuit
`1e-12 m^2` (default) | positive scalar

Laminar transition specification — Select how block transitions between the laminar and turbulent regimes
`Pressure ratio` (default) | `Reynolds number`

Laminar flow pressure ratio — Pressure ratio at which the flow transitions between laminar and turbulent regimes
`0.999` (default) | positive scalar in the range of [0,1]

Critical Reynolds number — Maximum Reynolds number for laminar flow
`12` (default) | positive scalar

Flow discharge coefficient — Semi-empirical parameter for valve capacity characterization
`0.7` (default) | positive scalar

Opening dynamics — Specify whether to include valve opening dynamics in simulation
`Do not include valve opening dynamics` (default) | `Include valve opening dynamics`

Opening time constant — Time constant for the first order response of the valve opening
`0.1 s` (default) | positive scalar

Initial area — Initial opening area of the valve
`1e-12 m^2` (default) | positive scalar

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.