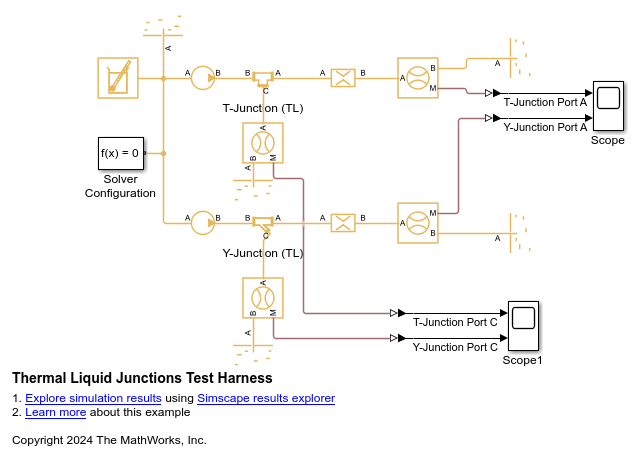
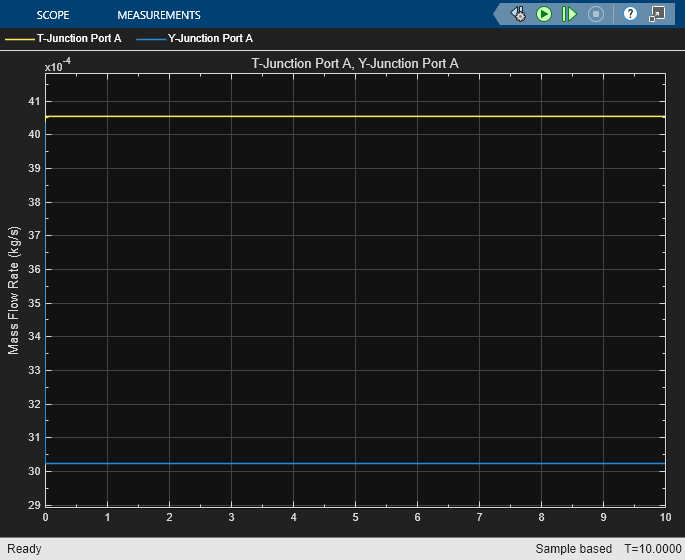
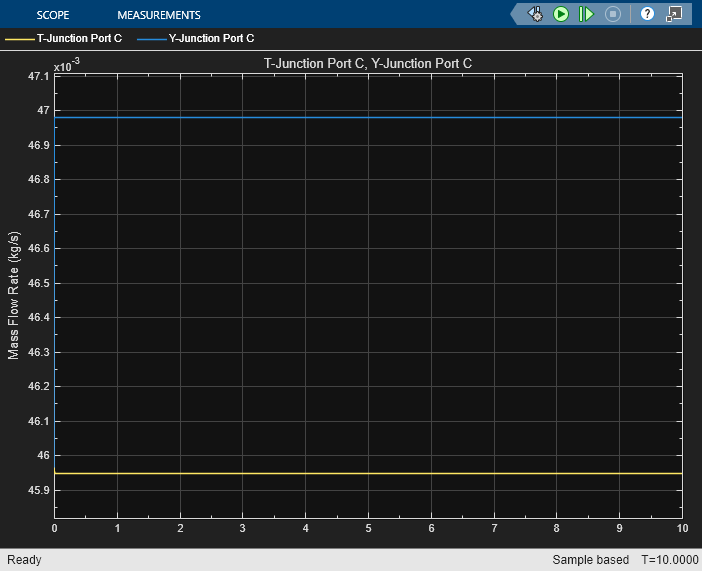
T-Junction (TL)

Three-way junction in a thermal liquid system

Since R2022a

Libraries:
Simscape / Fluids / Thermal Liquid / Pipes & Fittings

Description

The T-Junction (TL) block represents a three-way pipe junction with a branch line at port C connected at a 90° angle to the main pipe line, between ports A and B. You can specify a custom junction or a junction that uses a Rennels correlation or Crane correlation loss coefficient. When Loss coefficient model is set to Custom, you can specify the loss coefficients of each pipe segment for converging and diverging flows.

Flow Direction

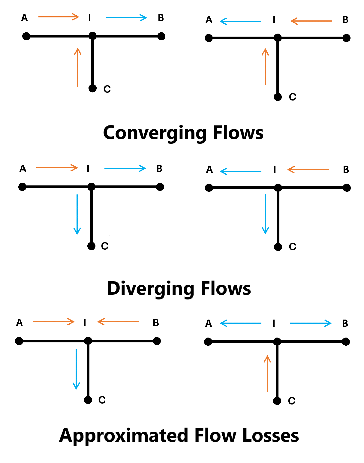
When the Loss coefficient model parameter is Crane correlation, Rennels correlation, or Custom, the block determines each loss coefficient based on the flow configuration. The flow is converging when the flow through port C merges into the main flow. The flow is diverging when the branch flow splits from the main flow. The flow direction between A and I, the point where the branch meets the main, and B and I must be consistent for all loss coefficients to be applied. If they are not, as shown in the last two diagrams in the figure below, the losses in the junction are approximated with the main branch loss coefficient for converging or diverging flows.

Diagram showing possible flow scenarios for the T-Junction block. In a converging flow, 2 perpendicular branch flows meet at the center node. In a diverging flow, one flow enters the center node and divides into the other two perpendicular flows. For flow losses, two parallel flows meet or diverge

The block uses mode charts to determine each loss coefficient for a given flow configuration. This table describes the conditions and coefficients for each operational mode.

Flow Scenario	ṁ_A	ṁ_B	ṁ_C	K_A	K_B	K_C
Stagnant	–	–	–	1 or last valid value	1 or last valid value	1 or last valid value
Diverging from node A	>ṁ_thresh	<-ṁ_thresh	<-ṁ_thresh	0	K_main,div	K_side,div
Diverging from node B	<-ṁ_thresh	>ṁ_thresh	<-ṁ_thresh	K_main,div	0	K_side,div
Converging to node A	<-ṁ_thresh	>ṁ_thresh	>ṁ_thresh	0	K_main,conv	K_side,conv
Converging to node B	>ṁ_thresh	<-ṁ_thresh	>ṁ_thresh	K_main,conv	0	K_side,conv
Converging to node C (branch) when the Loss coefficient model parameter is `Crane correlation` or `Custom`	>ṁ_thresh	>ṁ_thresh	<-ṁ_thresh	(K_main,conv + K_side,conv)/2	(K_main,conv + K_side,conv)/2	0
Diverging from node C (branch) when the Loss coefficient model parameter is `Crane correlation` or `Custom`	<-ṁ_thresh	<-ṁ_thresh	>ṁ_thresh	(K_main,div + K_side,div)/2	(K_main,div + K_side,div)/2	0

When the Loss coefficient model parameter Rennels correlation, the values for converging to node C (branch) and diverging from node C (branch) are calculated directly.

The flow is stagnant when the mass flow rate conditions do not match any defined flow scenario. Stagnant flow is permitted at the start of the simulation, but the block does not revert to stagnant flow after it has achieved another mode. The mass flow rate threshold, which is the point at which the flow in the pipe begins to reverse direction, is

${\dot{m}}_{t h r e s h} = {Re}_{c} υ \bar{ρ} \sqrt{\frac{π}{4} A_{\min}},$

where:

Re_c is the Critical Reynolds number, beyond which the transitional flow regime begins.
ν is the fluid viscosity.
$\bar{ρ}$ is the average fluid density.
A_min is the smallest cross-sectional area in the pipe junction.

Crane Correlation Coefficient Model

When you set the Loss coefficient model parameter to Crane correlation, the pipe loss coefficients, K_main and K_side, and the pipe friction factor, f_T, are calculated according to Crane [1] :

$K_{m a i n, d i v} = K_{m a i n, c o n v} = 20 f_{T, m a i n},$

$K_{s i d e, d i v} = K_{s i d e, c o n v} = 60 f_{T, s i d e} .$

In contrast to the custom junction type, the standard junction loss coefficient is the same for both converging and diverging flows. K_A, K_B, and K_C are then calculated in the same manner as custom junctions.

Nominal size (mm)	5	10	15	20	25	32	40	50	72.5	100	125	150	225	350	609.5
Friction factor, f_T	.035	.029	.027	.025	.023	.022	.021	.019	.018	.017	.016	.015	.014	.013	.012

Rennels Correlation Coefficient Model

When you set the Loss coefficient model parameter to Rennels correlation, the block calculates the pipe loss coefficients according to [2].

Diverging Flow on Main Branch

The main branch diverging loss coefficient is

$K_{m a i n, d i v} = 0.62 - 0.98 \frac{{\dot{m}}_{1}}{{\dot{m}}_{2}} + 0.36 {(\frac{{\dot{m}}_{1}}{{\dot{m}}_{2}})}^{2} + 0.03 {(\frac{{\dot{m}}_{2}}{{\dot{m}}_{1}})}^{6},$

where:

${\dot{m}}_{1}$ is the mass flow rate at the inflow of the main branch.
${\dot{m}}_{2}$ is the mass flow rate at the outflow of the main branch.

The value of K_main,div saturates when ${\dot{m}}_{2} / {\dot{m}}_{1}$ is equal to the value of the Minimum valid flow ratio for coefficient calculation parameter.

The side branch diverging loss coefficient is

$K_{s i d e, d i v} = (0.81 - 1.13 \frac{{\dot{m}}_{1}}{{\dot{m}}_{3}} + {(\frac{{\dot{m}}_{1}}{{\dot{m}}_{3}})}^{2}) {(\frac{d_{3}}{d_{1}})}^{4} + 1.12 \frac{d_{3}}{d_{1}} - 1.08 {(\frac{d_{3}}{d_{1}})}^{3} + K_{*},$

where

${\dot{m}}_{3}$ is the mass flow rate at the outflow of the side branch.
d₁ is the diameter of the main branch.
d₃ is the diameter of the side branch.
$K_{*} = 0.57 - 1.07 {(\frac{r}{d_{3}})}^{1 / 2} - 2.13 \frac{r}{d_{3}} + 8.24 {(\frac{r}{d_{3}})}^{3 / 2} - 8.48 {(\frac{r}{d_{3}})}^{2} + 2.90 {(\frac{r}{d_{3}})}^{5 / 2} .$
r is the value of the Junction radius of curvature parameter.

The value of K_side,div saturates when ${\dot{m}}_{3} / {\dot{m}}_{1}$ is equal to the value of the Minimum valid flow ratio for coefficient calculation parameter.

Converging Flow on Main Branch

The main branch converging loss coefficient is

$K_{m a i n, c o n v} = {(\frac{{\dot{m}}_{1}}{{\dot{m}}_{2}})}^{2} - 0.95 - 2 C_{x C} (\frac{{\dot{m}}_{1}}{{\dot{m}}_{2}} - 1) - 2 C_{M} ({(\frac{{\dot{m}}_{1}}{{\dot{m}}_{2}})}^{2} - \frac{{\dot{m}}_{1}}{{\dot{m}}_{2}}),$

where

$\begin{array}{l} C_{M} = 0.23 + 1.46 (\frac{r}{d_{3}}) - 2.75 {(\frac{r}{d_{3}})}^{2} + 1.65 {(\frac{r}{d_{3}})}^{3} \\ C_{x C} = 0.08 + 0.56 (\frac{r}{d_{3}}) - 1.75 {(\frac{r}{d_{3}})}^{2} + 1.83 {(\frac{r}{d_{3}})}^{3} \end{array}$

The value of K_main,conv saturates when ${\dot{m}}_{2} / {\dot{m}}_{1}$ is equal to the value of the Minimum valid flow ratio for coefficient calculation parameter.

The side branch converging loss coefficient is

$K_{s i d e, c o n v} = (2 C_{y C} - 1) + {(\frac{d_{3}}{d_{1}})}^{4} [2 (C_{x C} - 1) + 2 (2 - C_{x C} - C_{M}) \frac{{\dot{m}}_{1}}{{\dot{m}}_{3}} - 0.92 {(\frac{{\dot{m}}_{1}}{{\dot{m}}_{3}})}^{2}],$

where:

$C_{y C} = 1 - 0.25 {(\frac{d_{3}}{d_{1}})}^{1.3} - [0.11 \frac{r}{d_{3}} - 0.65 (\frac{r}{d_{3}}) + 0.83 {(\frac{r}{d_{3}})}^{3}] {(\frac{d_{3}}{d_{1}})}^{2} .$

The value of K_side,conv saturates when ${\dot{m}}_{3} / {\dot{m}}_{1}$ is equal to the value of the Minimum valid flow ratio for coefficient calculation parameter.

Converging or Diverging flow from Side Branch

The loss coefficient when the flow is converging to the side branch is

$K_{c o n v t o s i d e} = (0.81 - 1.16 \sqrt{\frac{r}{d}} + 0.5 \frac{r}{d}) {(\frac{{\dot{m}}_{1}}{{\dot{m}}_{2}})}^{2} - (0.95 - 1.65 \frac{r}{d}) \frac{{\dot{m}}_{1}}{{\dot{m}}_{2}} + 1.34 - 1.69 \frac{r}{d},$

where d is the diameter of the side branch. The value of K_{conv to side} saturates when ${\dot{m}}_{2} / {\dot{m}}_{1}$ is equal to the value of the Minimum valid flow ratio for coefficient calculation parameter.

The loss coefficient when the flow is diverging from the side branch is

$K_{d i v f r o m s i d e} = 0.59 {(\frac{{\dot{m}}_{1}}{{\dot{m}}_{2}})}^{2} + (1.18 - 1.84 \sqrt{\frac{r}{d}} + 1.16 \frac{r}{d}) \frac{{\dot{m}}_{1}}{{\dot{m}}_{2}} - 0.68 + 1.04 \sqrt{\frac{r}{d}} - 1.16 \frac{r}{d} .$

The value of K_{div from side} saturates when ${\dot{m}}_{2} / {\dot{m}}_{1}$ is equal to the value of the Minimum valid flow ratio for coefficient calculation parameter.

Custom T-Junction

When you set the Loss coefficient model parameter to Custom, the block calculates the pipe loss coefficient at each port, K, based on the user-defined loss parameters for converging and diverging flow and mass flow rate at each port. You must specify K_main,conv, K_main,div, K_side,conv, and K_side,div as the Main branch converging loss coefficient, Main branch diverging loss coefficient, Side branch converging loss coefficient, and Side branch diverging loss coefficient parameters, respectively.

Constant Coefficients T-Junction

When you set the Loss coefficient model parameter to Constant Coefficients, the block models the junction as a composite component of three Local Resistance (TL) blocks joined at a center node. When the block uses this setting, it does not use mode charts. Use this option if your model operates at nominal conditions and does not require high fidelity.

Mass and Momentum Balance

The block conserves mass in the junction such that

${\dot{m}}_{A} + {\dot{m}}_{B} + {\dot{m}}_{C} = 0.$

The block calculates the flow through the pipe junction using the momentum conservation equations between ports A, B, and C:

$\begin{array}{l} p_{A} - p_{I} = I_{A} + \frac{K_{A}}{2 \bar{ρ} A_{_{m a i n}}^{2}} {\dot{m}}_{A} \sqrt{{\dot{m}}_{A}^{2} + {\dot{m}}_{t h r e s h}^{2}} \\ p_{B} - p_{I} = I_{B} + \frac{K_{B}}{2 \bar{ρ} A_{_{m a i n}}^{2}} {\dot{m}}_{B} \sqrt{{\dot{m}}_{B}^{2} + {\dot{m}}_{t h r e s h}^{2}} \\ p_{C} - p_{I} = I_{C} + \frac{K_{C}}{2 \bar{ρ} A_{_{s i d e}}^{2}} {\dot{m}}_{C} \sqrt{{\dot{m}}_{C}^{2} + {\dot{m}}_{t h r e s h}^{2}} \end{array}$

where I represents the fluid inertia, and

$\begin{array}{l} I_{A} = {\ddot{m}}_{A} \frac{\sqrt{π \cdot A_{s i d e}}}{A_{m a i n}} \\ I_{B} = {\ddot{m}}_{B} \frac{\sqrt{π \cdot A_{s i d e}}}{A_{m a i n}} \\ I_{C} = {\ddot{m}}_{C} \frac{\sqrt{π \cdot A_{m a i n}}}{A_{s i d e}} \end{array}$

A_main is the Main branch area (A-B) parameter and A_side is the Side branch area (A-C, B-C) parameter.

Energy Balance

The block balances energy such that

$ϕ_{A} + ϕ_{B} + ϕ_{C} = 0,$

where:

ϕ_A is the energy flow rate at port A.
ϕ_B is the energy flow rate at port B.
ϕ_C is the energy flow rate at port C.

Variables

To set the priority and initial target values for the block variables prior to simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.

Nominal values provide a way to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. Nominal values can come from different sources, one of which is the Nominal Values section in the block dialog box or Property Inspector. For more information, see Modify Nominal Values for a Block Variable.

Ports

Conserving

expand all

A — Liquid port
thermal liquid

Thermal liquid conserving port associated with the liquid entrance or exit of the junction.

B — Liquid port
thermal liquid

Thermal liquid conserving port associated with the liquid entrance or exit of the junction.

C — Liquid port
thermal liquid

Thermal liquid conserving port associated with the liquid entrance or exit of the junction.

Parameters

expand all

Main branch area (A-B) — Cross-sectional area between ports A and B
`0.01 m^2` (default) | positive scalar

Area of connecting pipe between ports A and B.

Side branch area (A-C, B-C) — Cross-sectional area of the side branch
`0.01 m^2` (default) | positive scalar

Area of connecting pipe between ports A and C and between ports B and C.

Loss coefficient model — Loss coefficient type
`Crane correlation` (default) | `Rennels correlation` | `Custom` | `Constant Coefficients`

The junction loss coefficient model. Set this parameter to Custom to specify individual diverging and converging loss coefficients for each flow path segment.

Loss coefficient configuration change time constant — Time scale of smoothing function
`0.0001 s` (default) | positive scalar

Time scale of the smoothing function. Use this parameter to ensure smooth transitions by tuning the block dynamic behavior during flow reversals.

Dependencies

To enable this parameter, set Loss coefficient model to either Crane correlation, Rennels correlation, or Custom.

Critical Reynolds number — Upper Reynolds number limit for laminar flow
`150` (default) | positive scalar

Upper Reynolds number limit for laminar flow through the junction.

Zero-flow threshold Reynolds number — Reynolds number that corresponds to stagnant flow
`10` (default) | positive scalar

Reynolds number that the block uses to calculate the threshold beneath which the flow is stagnant. The block uses this threshold to reduce numerical chatter during simulation. This parameter does not have a physical meaning, but must be small in comparison to the expected mass flow rate values.

Dependencies

To enable this parameter, set Loss coefficient model to either Crane correlation, Rennels correlation, or Custom.

Main branch converging loss coefficient — Converging flow loss coefficient between A and B
`1.12` (default) | positive scalar

Loss coefficient for pressure loss calculations between ports A and B for converging flow.

Dependencies

To enable this parameter, set Loss coefficient model to Custom.

Main branch diverging loss coefficient — Diverging flow loss coefficient between A and B
`1.12` (default) | positive scalar

Loss coefficient for pressure loss calculations between ports A and B for diverging flow.

Dependencies

To enable this parameter, set Loss coefficient model to Custom.

Side branch converging loss coefficient — Converging flow loss coefficient between C and main
`1.12` (default) | positive scalar

Loss coefficient for pressure loss calculations between port C and the main line for converging flow.

Dependencies

To enable this parameter, set Loss coefficient model to Custom.

Side branch diverging loss coefficient — Diverging flow loss coefficient between C and main
`1.12` (default) | positive scalar

Loss coefficient for pressure loss calculations between port C and the main line for diverging flow.

Dependencies

To enable this parameter, set Loss coefficient model to Custom.

Junction radius of curvature — Radius of curvature of the junction
`0.001 m` (default) | positive scalar

Radius of the curvature of the junction used to calculate the loss coefficients when Loss coefficient model is set to Rennels correlation.

Dependencies

To enable this parameter, set Loss coefficient model to Rennels correlation.

Minimum valid flow ratio for coefficient calculation — Limit on flow ratios for coefficient calculations
`0.2` (default) | positive scalar

Minimum value for any flow ratio that the block uses to calculate loss coefficients. If the flow ratio is below this limit, it saturates at this value. The block uses this parameter to limit the impact of differences in flow magnitude between branches and to increase numerical stability if one branch has significantly less flow than others.

Only adjust this setting if your model has numerical stability problems.

Dependencies

To enable this parameter, set Loss coefficient model to Rennels correlation.

Smoothing factor — Numerical smoothing factor
`0.01` (default) | scalar between 0 and 1

Continuous smoothing factor that introduces a layer of gradual change to the flow response when it approaches the limit specified by the Minimum valid flow ratio for coefficient calculation parameter. Set this parameter to a nonzero value less than one to increase the stability of your simulation.

Only adjust this setting if your model has numerical stability problems.

Dependencies

To enable this parameter, set Loss coefficient model to Rennels correlation.

Fluid inertia — Option to model fluid inertia
`off` (default) | `on`

Whether to model fluid inertia, which lowers the risk of a block numerical issue during flow reversals. Avoid modeling fluid inertia unless it is numerically necessary, because it increases the computational cost.

Dependencies

To enable this parameter, set Loss coefficient model to Rennels correlation.

Loss coefficient A — Loss coefficient for branch A
`1` (default) | positive scalar

Loss coefficient for flow along branch A.

Dependencies

To enable this parameter, set Loss coefficient model to Constant Coefficients.

Loss coefficient B — Loss coefficient for branch B
`1` (default) | positive scalar

Loss coefficient for flow along branch B.

Dependencies

To enable this parameter, set Loss coefficient model to Constant Coefficients.

Loss coefficient C — Loss coefficient for branch C
`1` (default) | positive scalar

Loss coefficient for flow along branch C.

Dependencies

To enable this parameter, set Loss coefficient model to Constant Coefficients.

References

[1] Crane Co. Flow of Fluids Through Valves, Fittings, and Pipe TP-410. Crane Co., 1981.

[2] Rennels, D. C., & Hudson, H. M. Pipe flow: A practical and comprehensive guide. Hoboken, N.J: John Wiley & Sons., 2012.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2022a

expand all

R2024b: New model for constant loss coefficients

Set Loss coefficient model to Constant Coefficients to use a constant loss coefficient model. Use this option when your model does not require high fidelity.

R2024b: Robustness improvements enable block to more smoothly switch between mode chart states

The T-Junction (TL) block has new parameters and functionality that enable the block to more smoothly switch between states in mode charts. Adjust the Loss coefficient configuration change time constant parameter to control the time scale of the smoothing function. Use the Zero-flow threshold Reynold number parameter to calculate a non-zero mass flow rate threshold for stagnant flow. You can also now optionally model fluid inertia, which lowers the risk of a block numerical issue during flow reversals.

Results during flow reversals may be different than in previous releases. The behavior at steady-state conditions has not changed.

R2023a: New pipe loss coefficient models

The Three-way junction type parameter is renamed to the Loss coefficient model parameter. Set Three-way junction type to Rennels correlation to use the new loss coefficient model. The Standard option for this parameter is renamed to Crane correlation and the Custom option remains unchanged.

R2022b: Conversion to Mode Charts

The block uses mode charts to handle the different flow configurations. Results during flow scenario transitions may be different than in previous releases. Results during flow scenario transitions are not steady state and are not necessarily accurate.

T-Junction (TL)

Description

Flow Direction

Crane Correlation Coefficient Model

Rennels Correlation Coefficient Model

Custom T-Junction

Constant Coefficients T-Junction

Mass and Momentum Balance

Energy Balance

Variables

Ports

Conserving

A — Liquid port thermal liquid

B — Liquid port thermal liquid

C — Liquid port thermal liquid

Parameters

Main branch area (A-B) — Cross-sectional area between ports A and B 0.01 m^2 (default) | positive scalar

Side branch area (A-C, B-C) — Cross-sectional area of the side branch 0.01 m^2 (default) | positive scalar

Loss coefficient model — Loss coefficient type Crane correlation (default) | Rennels correlation | Custom | Constant Coefficients

Loss coefficient configuration change time constant — Time scale of smoothing function 0.0001 s (default) | positive scalar

Dependencies

Critical Reynolds number — Upper Reynolds number limit for laminar flow 150 (default) | positive scalar

Zero-flow threshold Reynolds number — Reynolds number that corresponds to stagnant flow 10 (default) | positive scalar

Dependencies

Main branch converging loss coefficient — Converging flow loss coefficient between A and B 1.12 (default) | positive scalar

Dependencies

Main branch diverging loss coefficient — Diverging flow loss coefficient between A and B 1.12 (default) | positive scalar

Dependencies

Side branch converging loss coefficient — Converging flow loss coefficient between C and main 1.12 (default) | positive scalar

Dependencies

Side branch diverging loss coefficient — Diverging flow loss coefficient between C and main 1.12 (default) | positive scalar

Dependencies

Junction radius of curvature — Radius of curvature of the junction 0.001 m (default) | positive scalar

Dependencies

Minimum valid flow ratio for coefficient calculation — Limit on flow ratios for coefficient calculations 0.2 (default) | positive scalar

Dependencies

Smoothing factor — Numerical smoothing factor 0.01 (default) | scalar between 0 and 1

Dependencies

Fluid inertia — Option to model fluid inertia off (default) | on

Dependencies

Loss coefficient A — Loss coefficient for branch A 1 (default) | positive scalar

Dependencies

Loss coefficient B — Loss coefficient for branch B 1 (default) | positive scalar

Dependencies

Loss coefficient C — Loss coefficient for branch C 1 (default) | positive scalar

Dependencies

References

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using Simulink® Coder™.

Version History

R2024b: New model for constant loss coefficients

R2024b: Robustness improvements enable block to more smoothly switch between mode chart states

R2023a: New pipe loss coefficient models

R2022b: Conversion to Mode Charts

See Also

Topics

A — Liquid port
thermal liquid

B — Liquid port
thermal liquid

C — Liquid port
thermal liquid

Main branch area (A-B) — Cross-sectional area between ports A and B
`0.01 m^2` (default) | positive scalar

Side branch area (A-C, B-C) — Cross-sectional area of the side branch
`0.01 m^2` (default) | positive scalar

Loss coefficient model — Loss coefficient type
`Crane correlation` (default) | `Rennels correlation` | `Custom` | `Constant Coefficients`

Loss coefficient configuration change time constant — Time scale of smoothing function
`0.0001 s` (default) | positive scalar

Critical Reynolds number — Upper Reynolds number limit for laminar flow
`150` (default) | positive scalar

Zero-flow threshold Reynolds number — Reynolds number that corresponds to stagnant flow
`10` (default) | positive scalar

Main branch converging loss coefficient — Converging flow loss coefficient between A and B
`1.12` (default) | positive scalar

Main branch diverging loss coefficient — Diverging flow loss coefficient between A and B
`1.12` (default) | positive scalar

Side branch converging loss coefficient — Converging flow loss coefficient between C and main
`1.12` (default) | positive scalar

Side branch diverging loss coefficient — Diverging flow loss coefficient between C and main
`1.12` (default) | positive scalar

Junction radius of curvature — Radius of curvature of the junction
`0.001 m` (default) | positive scalar

Minimum valid flow ratio for coefficient calculation — Limit on flow ratios for coefficient calculations
`0.2` (default) | positive scalar

Smoothing factor — Numerical smoothing factor
`0.01` (default) | scalar between 0 and 1

Fluid inertia — Option to model fluid inertia
`off` (default) | `on`

Loss coefficient A — Loss coefficient for branch A
`1` (default) | positive scalar

Loss coefficient B — Loss coefficient for branch B
`1` (default) | positive scalar

Loss coefficient C — Loss coefficient for branch C
`1` (default) | positive scalar

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.