Online State Estimation Using Identified Models - Nonlinear Models

This example uses:

This example describes how to generate the state-transition and measurement functions for online state and output estimation using nonlinear system identification techniques.

System Identification Toolbox™ provides several recursive algorithms for state estimation such as Kalman Filter, Extended Kalman Filter (EKF), Unscented Kalman Filter (UKF), and Particle Filter (PF). Use of a state estimator requires specification of state and measurement dynamics:

How the system advances the states, represented by the state-transition equation $X (k + 1) = f (X (k), \dots)$ , where $X (k)$ is the state value at the time step $k$ ; the function $f (\cdot)$ can accept additional input arguments to accommodate any dependency on exogenous inputs and the time instant.
How the system computes the output or measurement $y (k)$ as a function of $X (k)$ and possibly some additional inputs; $y (k) = g (X (k), \dots)$

In addition, you are required to provide the covariance values of the various disturbances affecting the state and measurement dynamics.

This example shows how you can generate the required state-transition and measurement equations by using nonlinear (black-box or grey-box) identification techniques. Four different modeling techniques are explored - Nonlinear ARX, Hammerstein-Wiener, Neural State Space and Nonlinear Grey Box.

This example describes:

How to extract, and separate out, the state-transition and measurement functions from identified nonlinear models of various types.
How to separate out noise dynamics in case the nonlinear model uses a nontrivial (that is, not an Output-Error structure) disturbance component; this is true only for the Nonlinear ARX models.
How to extend the nonlinear models of Output-Error structure in order to prescribe the state/process noise covariance required by the state estimators such as EKF.

Definition of an Output-Error Model Structure

A generic discrete-time dynamic model in the System Identification Toolbox has the following representation:

$y (t) = f (y (t - 1), y (t - 2), . . ., u (t), u (t - 1), . . . ., e (t), e (t - 1), . . .)$

where the function $f (.)$ relates the past values of the output $y (t)$ , the current/past values of the input $u (t)$ , and the disturbances current/past values $e (t)$ to the current value of the output. In the linear case, this can be written as a stochastic relationship using additive noise:

$y (t) = G (q) u (t) + H (q) e (t)$

where $G (q)$ , $H (q)$ are linear filters described by rational functions. When the noise filter $H (q) \equiv 1$ , the model is called an Output-Error model. This is because when $H (q)$ =1, the governing equation simplifies to:

$y (t) = G (q) u (t) + e (t)$

Here, the output at time $t$ is not affected by errors at previous time instants. In state-space form, this translates to a model of the form:

$\begin{array}{l} x (t + 1) = Ax (t) + B u (t) \\ y (t) = Cx (t) + Du (t) + e (t) \end{array}$

This is a system with no process noise. A state estimator based on this model cannot correct the state predictions using current output measurements. Hence an Output-Error model needs to extended in some way to extract the process noise information.

Most nonlinear models in the System Identification Toolbox are of Output-Error structure. The only exception is Nonlinear ARX models, where the model structure is:

$y (t) = f (y (t - 1), y (t - 2), . . ., u (t), u (t - 1)) + e (t)$

where $y (t)$ are measured (noise-corrupted) outputs values. The influence of past errors $e (t - 1), e (t - 2), . . .$ can be seen more clearly by writing the equation in terms of the true (noise free) output $y_{0} (t)$ , so that $y (t) = y_{0} (t) + e (t)$ :

$y_{0} (t) = f (y_{0} (t - 1) + e (t - 1), y_{0} (t - 2) + e (t - 2), . . ., u (t), u (t - 1))$

Example System: An Industrial Robot Arm

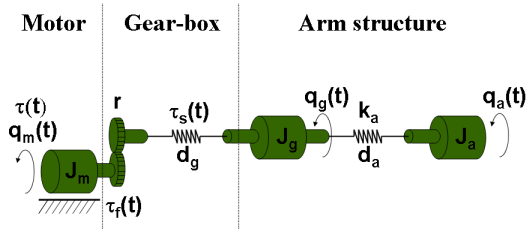
Consider a robot arm is described by a nonlinear three-mass flexible model. The input to the robot is the applied torque $u (t) = τ (t)$ generated by the electrical motor, and the resulting angular velocity of the motor $y (t) = \frac{d}{d t} q_{m} (t)$ is the measured output.

It is possible to derive the equations of motion for this system. For example a nonlinear state-space description of this system uses 5 states. For more information on this system, see the example titled "Modeling an Industrial Robot Arm".

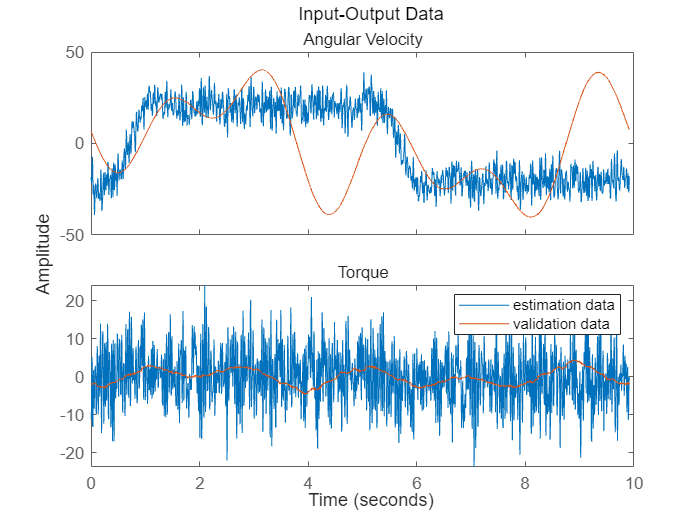
This system is excited with inputs of different profiles and the resulting angular velocity of the motor recorded. A periodic excitation signal with approximately 10 seconds duration was employed to generate a reference speed for the controller. The chosen sampling frequency was 2 kHz (sample time, Ts = 0.0005 seconds). For estimation (training) data, a multisine input signal with a flat amplitude spectrum in the frequency interval 1-40 Hz with a peak value of 16 rad/s was used. The multisine signal is superimposed on a filtered square wave with amplitude 20 rad/s and cut-off frequency 1 Hz. For validation data, a multisine input signal containing frequencies 0.1, 0.3, and 0.5 Hz was used, with peak value 40 rad/s.

Both datasets are downsampled 10 times for the purposes of the current example.

load robotarmdata.mat
% Prepare estimation data
eData = iddata(ye,ue,5e-4,'InputName','Torque','OutputName','Angular Velocity','Tstart',0);
eData = idresamp(eData,[1 10]);
eData.Name = 'estimation data'

eData =

Time domain data set with 1984 samples.  
Sample time: 0.005 seconds                
Name: estimation data                     
                                          
Outputs                Unit (if specified)
   Angular Velocity                       
                                          
Inputs                 Unit (if specified)
   Torque                                 
                                          
Data Properties

% Prepare validation data
vData = iddata(yv3,uv3,5e-4,'InputName','Torque','OutputName','Angular Velocity','Tstart',0);
vData = idresamp(vData,[1 10]);
vData.Name = 'validation data';
idplot(eData, vData)
legend show

Nonlinear Black Box Model

Suppose you have prior knowledge that the underlying process is nonlinear (or that the linear black box model does not provide a good result), but you do not have detailed knowledge of the underlying physics. In that case you can identify nonlinear black-box models of different structures. Then use the identified models to build up the state estimators.

Nonlinear ARX Model

A nonlinear ARX model is a discrete-time model that has the following structure:

$y (t) = f (y (t - 1), y (t - 2), . . ., u (t), u (t - 1)) + e (t)$

That is, the output at time $t$ is computed as a nonlinear function of past outputs and present and past inputs. At any time step the disturbance $e (t)$ gets added to the output. All future values $y (t + 1), y (t + 2), \dots$ would typically contain the effect of this disturbance since the past outputs are used to compute the future ones. In a sense, the effect of disturbances accumulate as time progresses. As a result, long-term predictions are usually harder with these models especially if they have been trained in open loop (for example, by using Focus = 'prediction' with the nlarx command).

IDNLARX Model States

The states of this model are defined as the lagged input/output variables. So a nonlinear ARX model using the equation:

$y (t) = f (y (t - 1), u (t), u (t - 2)) + e (t)$

can be expressed in state-space form by using the state variables:

$\begin{array}{l} x_{1} (t) = y (t - 1) \\ x_{2} (t) = u (t - 1) \\ x_{3} (t) = u (t - 2) \end{array}$

leading to the following state-space representation:

$x_{1} (t + 1) = f (x_{1} (t), x_{3} (t), u (t)) + e (t)$

$x_{2} (t + 1) = u (t)$

$x_{3} (t + 1) = x_{2} (t)$

$y (t) = x_{1} (t + 1) = f (x_{1} (t), x_{3} (t), u (t)) + e (t)$

Define $X (t) = [x_{1} (t), x_{2} (t), x_{3} (t)]^{T}$ . Then in the matrix form you have the following representation:

$\begin{array}{l} X (t + 1) = F (X (t), u (t)) + K e (t) \\ y (t) = f (X (t), u (t)) + e (t) \end{array}$

where $K = [1, 0, 0]^{T}$ is a constant matrix, and the vector function $F (.) = {[f (.), u (t), x_{2} (t)]}^{T}$ . Note that in this form, the process and measurement noises are correlated.

Identification of Wavelet Network Based Nonlinear ARX Model

Identify a Nonlinear ARX model for the robot arm data.

vars = {'Angular Velocity','Torque'};
L = linearRegressor(vars,1:2:8);
P = polynomialRegressor(vars,1:2:8,3);
opt = nlarxOptions(SearchMethod='gna',Focus='simulation');
nlarx1 = nlarx(eData, [L;P], idWaveletNetwork(3), opt)

nlarx1 =

Nonlinear ARX model with 1 output and 1 input
  Inputs: Torque
  Outputs: Angular Velocity

Regressors:
  1. Linear regressors in variables Angular Velocity, Torque
  2. Order 3 regressors in variables Angular Velocity, Torque
  List of all regressors

Output function: Wavelet network with 3 units
Sample time: 0.005 seconds

Status:                                                                            
Termination condition: No improvement along the search direction with line search..
Number of iterations: 6, Number of function evaluations: 129                       
                                                                                   
Estimated using NLARX on time domain data "estimation data".                       
Fit to estimation data: 78.18% (simulation focus)                                  
FPE: 6.334, MSE: 20.65                                                             
More information in model's "Report" property.

Model Properties

% Perform 10 step ahead prediction for the output data in the validation dataset.
compare(vData, nlarx1, 10);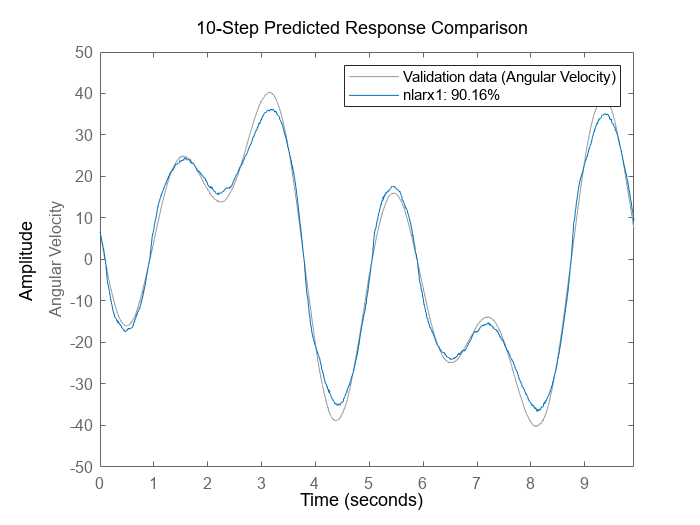

Using the Model in the Extended Kalman Filter (EKF) Block

In order to use this model in the EKF block, you need to specify the state-transition and measurement functions as Simulink functions. For the current example, these are implemented using MATLAB Function Blocks. The nlarxPredictFcn function performs the core computation; this function is called by the MATLAB Function blocks implementing the state transition and measurement updates.

type nlarxPredictFcn

function [y,xnext] = nlarxPredictFcn(x,u)
% Predict the states and output of a nonlinear ARX model.
% The identified model ("nlarx1") is assumed to be available in the MATLAB base workspace.

%  Copyright 2022 The MathWorks, Inc.

sys = evalin('base','nlarx1');

% Step 1: Compute model regressors as a function of states. Use GETERG to see the list of
% regressors. Regressors are non-tunable, static functions of model states and inputs.
I = [1 3 5 7 8 10 12 14];
R = [x(I,:); x(I,:).^3].';

% Step 2: Map the regressors to the model output. This is required since x1(t+1) = y(t) for this
% model. Note that output y is a static function (represented by the wavelet network) of the model's
% regressors (R).
N = sys.Normalization;
NL = sys.OutputFcn;
R = (R-N.RegressorCenter)./N.RegressorScale;
y = evaluate(NL, R);
y = (y.*N.OutputScale + N.OutputCenter).';

if nargout>1
   % Compose the output xnext := x(t+1)
   xnext = x; % initialization
   xnext(1,:) = y;
   xnext(2:7,:) = x(1:6,:);
   xnext(8,:) = u;
   xnext(9:14,:) = xnext(8:13,:);
end

The state estimation scenario based on the identified model (nlarx1) is implemented in the Simulink model StateEstimation_Using_NonlinearARX.slx. The scenario considered is 10-step ahead prediction realized by enabling the multi-rate operation; the measurements are used for correction of the state estimates only once for every 10 successive predictions.

% Prepare some data for the EKF Block
NV = nlarx1.NoiseVariance; % measurement noise variance
K = zeros(14,1); % (there are 14 states)
K(1) = 1;
StateNoiseCovariance = K*NV*K';
Ts = nlarx1.Ts;  % prediction time interval
Ts2 = 10*Ts;     % correction time interval

open_system('StateEstimation_Using_NonlinearARX')

Using the Model in the Unscented Kalman Filter (UKF) Block

The UKF block is configured in the same manner as the EKF block. The Simulink functions stateTransitionFcn and measurementFcn in the model StateEstimation_Using_NonlinearARX.slx are used by both the EKF and UKF blocks.

Using the Model in the Particle Filter (PF) Block

For the Particle Filter block, you need to specify the transition function for the particles and the value of the measurement likelihood as a probability distribution.

NumParticles = 1000; % number of particles used by the Particle filter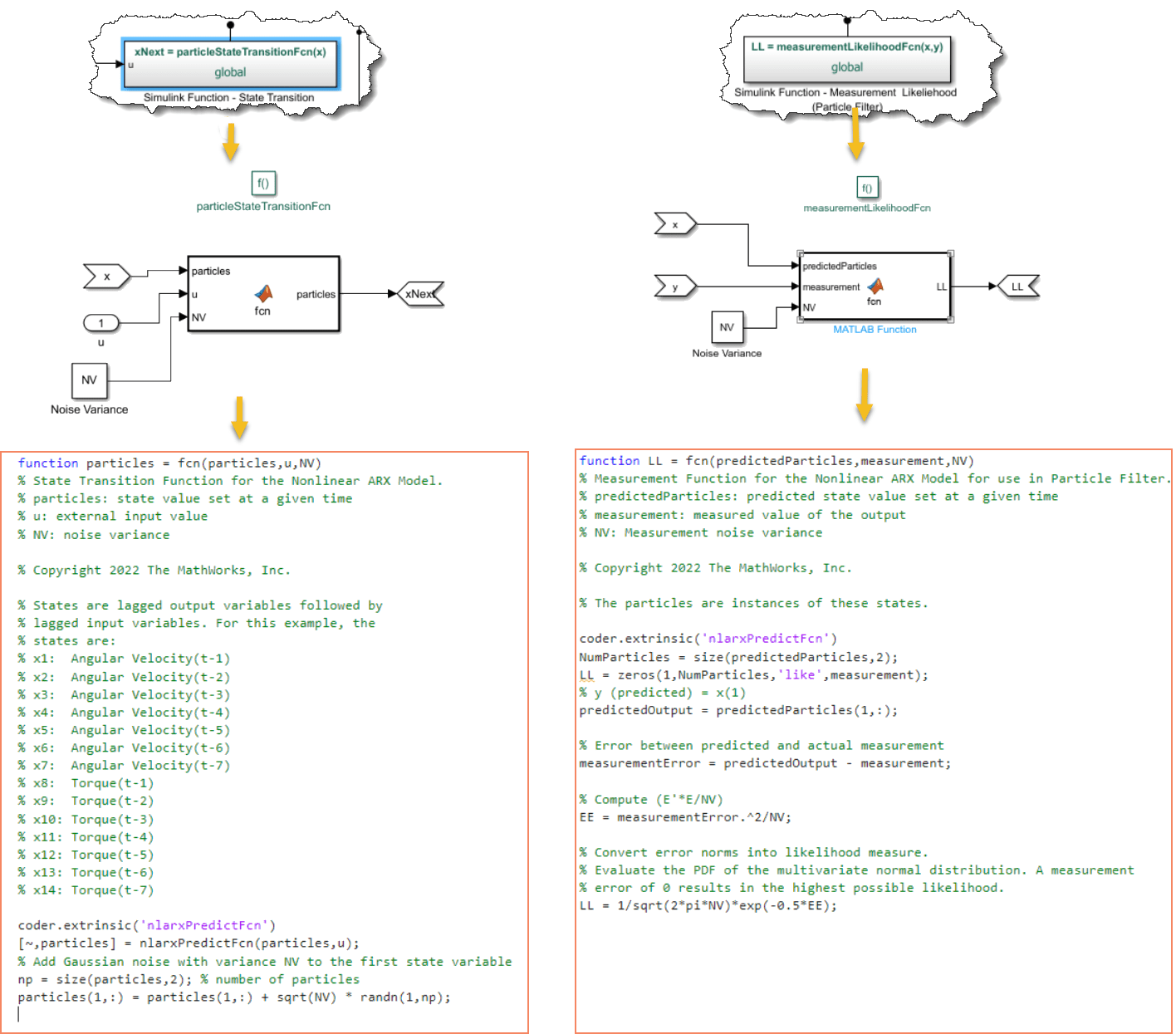

10 Step Ahead State Estimation Results

sim('StateEstimation_Using_NonlinearARX');

For this example, the three state estimators perform similarly. Note that the system output is same as the first state value. The filters underestimate the outputs at certain regions of rapid change. This observation is consistent with the direct 10-steap ahead prediction result shown in the compare plot.

Hammerstein Wiener Model

Another popular type of nonlinear dynamic model is a Hammerstein-Wiener model. It connects static nonlinear functions in series with a linear transfer function. The states of this model are the states of its linear block.

% Estimate a model that uses piecewise linear functions for its input and output nonlinearities
nlhw1 = nlhw(eData,[7 7 1])

nlhw1 =

Hammerstein-Wiener model with 1 output and 1 input

Linear transfer function corresponding to the orders nb = 7, nf = 7, nk = 1

Input nonlinearity: Piecewise linear with 10 break-points
Output nonlinearity: Piecewise linear with 10 break-points
Sample time: 0.005 seconds

Status:                                                      
Termination condition: Maximum number of iterations reached..
Number of iterations: 20, Number of function evaluations: 116
                                                             
Estimated using NLHW on time domain data "estimation data".  
Fit to estimation data: 89.91%                               
FPE: 4.674, MSE: 4.413                                       
More information in model's "Report" property.

Model Properties

compare(vData, nlhw1) % validate the model quality on an independent dataset

A Hammerstein Wiener model is an output-error model; there is no process noise. However, one can consider extending the identified model by prescribing process noise of non-zero covariance (covariance value determination would require a separate analysis). For this example, this extension is not explored.

uNL = nlhw1.InputNonlinearity;
yNL = nlhw1.OutputNonlinearity;
linTF = nlhw1.LinearModel;
[A,B,C,D] = ssdata(linTF);
Ts = nlhw1.Ts;

For using this model for state estimation, you can use the intermediate signal w(t) as the input signal since the I/O nonlinearities do not contain any states.

t = vData.SamplingInstants; % the time vector for the validation data
u = vData.InputData; % the input signal u(t)
w = evaluate(uNL, u); % the output of the "Input Nonlinearity f" block w(t)

The model states can be obtained by simulating the linear block using the signal w(t) and any prescribed initial conditions. For example:

[~,~,x] = sim(nlhw1, w);
plot(t,x)
xlabel('Time (seconds)')
ylabel('States (X)')

shows the state trajectories generated for zero initial conditions.

Since there is no process noise, there is no correction step required in the state predictors. The entire state prediction exercise is same as a pure simulation. The state estimators such as EKF are required only when there is an opportunity to correct the estimates using the measurements. This is explored more in the context of state-space models.

Nonlinear State Space Models

Neural State Space Model

A neural state space model is a continuous- or discrete-time nonlinear model where you specify the state transition and measurement functions as multi-layer feedforward neural networks. This modeling technique requires Deep Learning Toolbox™. Neural state space models are output-error models - they assume the states are not affected by process noise.

Training a neural state space model requires measurements of the states as well as the outputs. Assume that the state definitions are not available. Hence define states in terms of lagged inputs and outputs. You can generate data for the lagged variables by using the getreg command that is called on a template Nonlinear ARX model that uses the regressors defined as the lagged variables.

eData2 = idresamp(eData,[1 2]); % reduce data for quicker results

% normalize the data
eM = mean([eData2.OutputData,eData2.InputData]);
eSD = std([eData2.OutputData,eData2.InputData]);
eData2.OutputData = (eData2.OutputData-eM(1))/eSD(1);
eData2.InputData = (eData2.InputData-eM(2))/eSD(2);

Ts = eData2.Ts;
vars = {'Angular Velocity','Torque'};
nx = 7;
L = linearRegressor(vars,1:nx);
n0 = idnlarx(vars(1),vars(2),L,'Ts',Ts);
% View the state variables
States = getreg(n0); % there are 8 states
disp(strjoin(States,'\n'))

Angular Velocity(t-1)
Angular Velocity(t-2)
Angular Velocity(t-3)
Angular Velocity(t-4)
Angular Velocity(t-5)
Angular Velocity(t-6)
Angular Velocity(t-7)
Torque(t-1)
Torque(t-2)
Torque(t-3)
Torque(t-4)
Torque(t-5)
Torque(t-6)
Torque(t-7)

% get training data corresponding to these states
XData = getreg(n0, eData2);

% convert data into an iddata object; add the actual output (Angular Velocity(t)) as the last
% output signal
ymeas = eData2.OutputData;
xmeas = XData{:,:};
XYData = iddata([xmeas,ymeas],eData2.InputData,...
   'OutputName',[States; vars(1)],'InputName',vars(2),'Ts',Ts,'Tstart',0);

% Discard first 4 samples that contain effects of unknown initial conditions
XYData = XYData(nx+1:end);

Create a Neural State Space model that uses 14 states and one input. Since the states are considered measured, the model has 15 outputs, one corresponding to each state, plus the actual output.

nss = idNeuralStateSpace(numel(States),NumInputs=1,NumOutputs=numel(States)+1,Ts=Ts);

Model the state-transition function as a 1 hidden layer network using sigmoid activation layer.

rng(5) % for reproducibility
nss.StateNetwork = createMLPNetwork(nss,'state', ...
    LayerSizes=numel(States), ...
    Activations="sigmoid", ...
    WeightsInitializer="glorot", ...
    BiasInitializer="zeros");
summary(nss.StateNetwork)

   Initialized: true

   Number of learnables: 434

   Inputs:
      1   'x[k]'   14 features
      2   'u[k]'   1 features

The first 14 outputs are the states themselves Hence nss.OutputNetwork(1) is a trivial network representing the equation $y_{1} (t) = x (t)$ . The 15th output of this model represents the true measured output $y_{2} (t) = y (t)$ . For this output, create a separate, single hidden layer feedforward network using tanh activation layer.

nss.OutputNetwork(2) = createMLPNetwork(nss,'output', ...
    LayerSizes=1, ...
    Activations="sigmoid", ...
    WeightsInitializer="ones", ...
    BiasInitializer="zeros");
summary(nss.OutputNetwork(2))

   Initialized: true

   Number of learnables: 17

   Inputs:
      1   'x[k]'   14 features
      2   'u[k]'   1 features

Prepare training data by splitting it into 4 overlapping segments.

NumBatches = 4;
Ns = size(XYData,1);
Nsb = 300;
Data = cell(1,NumBatches);
pt = 0;
for i = 1:NumBatches
   if pt+Nsb<=Ns
      Data{i} = XYData(pt+(1:Nsb));
   else
      Data{i} = XYData(pt+1:end);
   end
   Data{i}.Tstart = 0;
   pt = pt + Nsb-20; % 20 sample overlap
end
Data = merge(Data{:});

Prepare training options. Choose ADAM Solver and increase the learning rate to 0.002. Also set other options such as maximum number of epochs to run and the frequency of validation plot update.

opt = nssTrainingOptions('adam');
opt.MaxEpochs = 1500;
opt.MiniBatchSize = Nsb;
opt.LearnRate = 0.02;

Train the model, where you use the last experiment in Data for in-estimation cross validation.

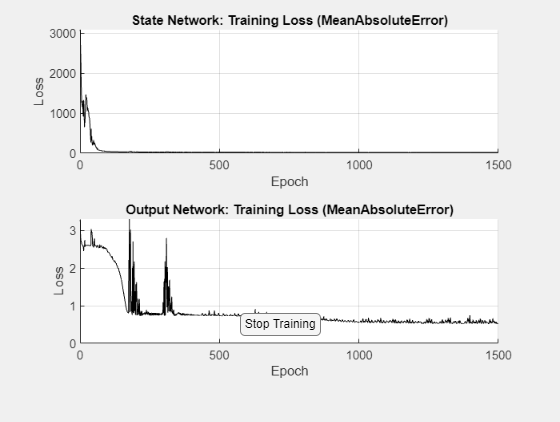
tic
nss = nlssest(Data,nss,opt,UseLastExperimentForValidation=true)

Training in progress (completed epoch/max epochs):        0/    1500       1/    1500       2/    1500       3/    1500       4/    1500       5/    1500       6/    1500       7/    1500       8/    1500       9/    1500      10/    1500      11/    1500      12/    1500      13/    1500      14/    1500      15/    1500      16/    1500      17/    1500      18/    1500      19/    1500      20/    1500      21/    1500      22/    1500      23/    1500      24/    1500      25/    1500      26/    1500      27/    1500      28/    1500      29/    1500      30/    1500      31/    1500      32/    1500      33/    1500      34/    1500      35/    1500      36/    1500      37/    1500      38/    1500      39/    1500      40/    1500      41/    1500      42/    1500      43/    1500      44/    1500      45/    1500      46/    1500      47/    1500      48/    1500      49/    1500      50/    1500      51/    1500      52/    1500      53/    1500      54/    1500      55/    1500      56/    1500      57/    1500      58/    1500      59/    1500      60/    1500      61/    1500      62/    1500      63/    1500      64/    1500      65/    1500      66/    1500      67/    1500      68/    1500      69/    1500      70/    1500      71/    1500      72/    1500      73/    1500      74/    1500      75/    1500      76/    1500      77/    1500      78/    1500      79/    1500      80/    1500      81/    1500      82/    1500      83/    1500      84/    1500      85/    1500      86/    1500      87/    1500      88/    1500      89/    1500      90/    1500      91/    1500      92/    1500      93/    1500      94/    1500      95/    1500      96/    1500      97/    1500      98/    1500      99/    1500     100/    1500     101/    1500     102/    1500     103/    1500     104/    1500     105/    1500     106/    1500     107/    1500     108/    1500     109/    1500     110/    1500     111/    1500     112/    1500     113/    1500     114/    1500     115/    1500     116/    1500     117/    1500     118/    1500     119/    1500     120/    1500     121/    1500     122/    1500     123/    1500     124/    1500     125/    1500     126/    1500     127/    1500     128/    1500     129/    1500     130/    1500     131/    1500     132/    1500     133/    1500     134/    1500     135/    1500     136/    1500     137/    1500     138/    1500     139/    1500     140/    1500     141/    1500     142/    1500     143/    1500     144/    1500     145/    1500     146/    1500     147/    1500     148/    1500     149/    1500     150/    1500     151/    1500     152/    1500     153/    1500     154/    1500     155/    1500     156/    1500     157/    1500     158/    1500     159/    1500     160/    1500     161/    1500     162/    1500     163/    1500     164/    1500     165/    1500     166/    1500     167/    1500     168/    1500     169/    1500     170/    1500     171/    1500     172/    1500     173/    1500     174/    1500     175/    1500     176/    1500     177/    1500     178/    1500     179/    1500     180/    1500     181/    1500     182/    1500     183/    1500     184/    1500     185/    1500     186/    1500     187/    1500     188/    1500     189/    1500     190/    1500     191/    1500     192/    1500     193/    1500     194/    1500     195/    1500     196/    1500     197/    1500     198/    1500     199/    1500     200/    1500     201/    1500     202/    1500     203/    1500     204/    1500     205/    1500     206/    1500     207/    1500     208/    1500     209/    1500     210/    1500     211/    1500     212/    1500     213/    1500     214/    1500     215/    1500     216/    1500     217/    1500     218/    1500     219/    1500     220/    1500     221/    1500     222/    1500     223/    1500     224/    1500     225/    1500     226/    1500     227/    1500     228/    1500     229/    1500     230/    1500     231/    1500     232/    1500     233/    1500     234/    1500     235/    1500     236/    1500     237/    1500     238/    1500     239/    1500     240/    1500     241/    1500     242/    1500     243/    1500     244/    1500     245/    1500     246/    1500     247/    1500     248/    1500     249/    1500     250/    1500     251/    1500     252/    1500     253/    1500     254/    1500     255/    1500     256/    1500     257/    1500     258/    1500     259/    1500     260/    1500     261/    1500     262/    1500     263/    1500     264/    1500     265/    1500     266/    1500     267/    1500     268/    1500     269/    1500     270/    1500     271/    1500     272/    1500     273/    1500     274/    1500     275/    1500     276/    1500     277/    1500     278/    1500     279/    1500     280/    1500     281/    1500     282/    1500     283/    1500     284/    1500     285/    1500     286/    1500     287/    1500     288/    1500     289/    1500     290/    1500     291/    1500     292/    1500     293/    1500     294/    1500     295/    1500     296/    1500     297/    1500     298/    1500     299/    1500     300/    1500     301/    1500     302/    1500     303/    1500     304/    1500     305/    1500     306/    1500     307/    1500     308/    1500     309/    1500     310/    1500     311/    1500     312/    1500     313/    1500     314/    1500     315/    1500     316/    1500     317/    1500     318/    1500     319/    1500     320/    1500     321/    1500     322/    1500     323/    1500     324/    1500     325/    1500     326/    1500     327/    1500     328/    1500     329/    1500     330/    1500     331/    1500     332/    1500     333/    1500     334/    1500     335/    1500     336/    1500     337/    1500     338/    1500     339/    1500     340/    1500     341/    1500     342/    1500     343/    1500     344/    1500     345/    1500     346/    1500     347/    1500     348/    1500     349/    1500     350/    1500     351/    1500     352/    1500     353/    1500     354/    1500     355/    1500     356/    1500     357/    1500     358/    1500     359/    1500     360/    1500     361/    1500     362/    1500     363/    1500     364/    1500     365/    1500     366/    1500     367/    1500     368/    1500     369/    1500     370/    1500     371/    1500     372/    1500     373/    1500     374/    1500     375/    1500     376/    1500     377/    1500     378/    1500     379/    1500     380/    1500     381/    1500     382/    1500     383/    1500     384/    1500     385/    1500     386/    1500     387/    1500     388/    1500     389/    1500     390/    1500     391/    1500     392/    1500     393/    1500     394/    1500     395/    1500     396/    1500     397/    1500     398/    1500     399/    1500     400/    1500     401/    1500     402/    1500     403/    1500     404/    1500     405/    1500     406/    1500     407/    1500     408/    1500     409/    1500     410/    1500     411/    1500     412/    1500     413/    1500     414/    1500     415/    1500     416/    1500     417/    1500     418/    1500     419/    1500     420/    1500     421/    1500     422/    1500     423/    1500     424/    1500     425/    1500     426/    1500     427/    1500     428/    1500     429/    1500     430/    1500     431/    1500     432/    1500     433/    1500     434/    1500     435/    1500     436/    1500     437/    1500     438/    1500     439/    1500     440/    1500     441/    1500     442/    1500     443/    1500     444/    1500     445/    1500     446/    1500     447/    1500     448/    1500     449/    1500     450/    1500     451/    1500     452/    1500     453/    1500     454/    1500     455/    1500     456/    1500     457/    1500     458/    1500     459/    1500     460/    1500     461/    1500     462/    1500     463/    1500     464/    1500     465/    1500     466/    1500     467/    1500     468/    1500     469/    1500     470/    1500     471/    1500     472/    1500     473/    1500     474/    1500     475/    1500     476/    1500     477/    1500     478/    1500     479/    1500     480/    1500     481/    1500     482/    1500     483/    1500     484/    1500     485/    1500     486/    1500     487/    1500     488/    1500     489/    1500     490/    1500     491/    1500     492/    1500     493/    1500     494/    1500     495/    1500     496/    1500     497/    1500     498/    1500     499/    1500     500/    1500     501/    1500     502/    1500     503/    1500     504/    1500     505/    1500     506/    1500     507/    1500     508/    1500     509/    1500     510/    1500     511/    1500     512/    1500     513/    1500     514/    1500     515/    1500     516/    1500     517/    1500     518/    1500     519/    1500     520/    1500     521/    1500     522/    1500     523/    1500     524/    1500     525/    1500     526/    1500     527/    1500     528/    1500     529/    1500     530/    1500     531/    1500     532/    1500     533/    1500     534/    1500     535/    1500     536/    1500     537/    1500     538/    1500     539/    1500     540/    1500     541/    1500     542/    1500     543/    1500     544/    1500     545/    1500     546/    1500     547/    1500     548/    1500     549/    1500     550/    1500     551/    1500     552/    1500     553/    1500     554/    1500     555/    1500     556/    1500     557/    1500     558/    1500     559/    1500     560/    1500     561/    1500     562/    1500     563/    1500     564/    1500     565/    1500     566/    1500     567/    1500     568/    1500     569/    1500     570/    1500     571/    1500     572/    1500     573/    1500     574/    1500     575/    1500     576/    1500     577/    1500     578/    1500     579/    1500     580/    1500     581/    1500     582/    1500     583/    1500     584/    1500     585/    1500     586/    1500     587/    1500     588/    1500     589/    1500     590/    1500     591/    1500     592/    1500     593/    1500     594/    1500     595/    1500     596/    1500     597/    1500     598/    1500     599/    1500     600/    1500     601/    1500     602/    1500     603/    1500     604/    1500     605/    1500     606/    1500     607/    1500     608/    1500     609/    1500     610/    1500     611/    1500     612/    1500     613/    1500     614/    1500     615/    1500     616/    1500     617/    1500     618/    1500     619/    1500     620/    1500     621/    1500     622/    1500     623/    1500     624/    1500     625/    1500     626/    1500     627/    1500     628/    1500     629/    1500     630/    1500     631/    1500     632/    1500     633/    1500     634/    1500     635/    1500     636/    1500     637/    1500     638/    1500     639/    1500     640/    1500     641/    1500     642/    1500     643/    1500     644/    1500     645/    1500     646/    1500     647/    1500     648/    1500     649/    1500     650/    1500     651/    1500     652/    1500     653/    1500     654/    1500     655/    1500     656/    1500     657/    1500     658/    1500     659/    1500     660/    1500     661/    1500     662/    1500     663/    1500     664/    1500     665/    1500     666/    1500     667/    1500     668/    1500     669/    1500     670/    1500     671/    1500     672/    1500     673/    1500     674/    1500     675/    1500     676/    1500     677/    1500     678/    1500     679/    1500     680/    1500     681/    1500     682/    1500     683/    1500     684/    1500     685/    1500     686/    1500     687/    1500     688/    1500     689/    1500     690/    1500     691/    1500     692/    1500     693/    1500     694/    1500     695/    1500     696/    1500     697/    1500     698/    1500     699/    1500     700/    1500     701/    1500     702/    1500     703/    1500     704/    1500     705/    1500     706/    1500     707/    1500     708/    1500     709/    1500     710/    1500     711/    1500     712/    1500     713/    1500     714/    1500     715/    1500     716/    1500     717/    1500     718/    1500     719/    1500     720/    1500     721/    1500     722/    1500     723/    1500     724/    1500     725/    1500     726/    1500     727/    1500     728/    1500     729/    1500     730/    1500     731/    1500     732/    1500     733/    1500     734/    1500     735/    1500     736/    1500     737/    1500     738/    1500     739/    1500     740/    1500     741/    1500     742/    1500     743/    1500     744/    1500     745/    1500     746/    1500     747/    1500     748/    1500     749/    1500     750/    1500     751/    1500     752/    1500     753/    1500     754/    1500     755/    1500     756/    1500     757/    1500     758/    1500     759/    1500     760/    1500     761/    1500     762/    1500     763/    1500     764/    1500     765/    1500     766/    1500     767/    1500     768/    1500     769/    1500     770/    1500     771/    1500     772/    1500     773/    1500     774/    1500     775/    1500     776/    1500     777/    1500     778/    1500     779/    1500     780/    1500     781/    1500     782/    1500     783/    1500     784/    1500     785/    1500     786/    1500     787/    1500     788/    1500     789/    1500     790/    1500     791/    1500     792/    1500     793/    1500     794/    1500     795/    1500     796/    1500     797/    1500     798/    1500     799/    1500     800/    1500     801/    1500     802/    1500     803/    1500     804/    1500     805/    1500     806/    1500     807/    1500     808/    1500     809/    1500     810/    1500     811/    1500     812/    1500     813/    1500     814/    1500     815/    1500     816/    1500     817/    1500     818/    1500     819/    1500     820/    1500     821/    1500     822/    1500     823/    1500     824/    1500     825/    1500     826/    1500     827/    1500     828/    1500     829/    1500     830/    1500     831/    1500     832/    1500     833/    1500     834/    1500     835/    1500     836/    1500     837/    1500     838/    1500     839/    1500     840/    1500     841/    1500     842/    1500     843/    1500     844/    1500     845/    1500     846/    1500     847/    1500     848/    1500     849/    1500     850/    1500     851/    1500     852/    1500     853/    1500     854/    1500     855/    1500     856/    1500     857/    1500     858/    1500     859/    1500     860/    1500     861/    1500     862/    1500     863/    1500     864/    1500     865/    1500     866/    1500     867/    1500     868/    1500     869/    1500     870/    1500     871/    1500     872/    1500     873/    1500     874/    1500     875/    1500     876/    1500     877/    1500     878/    1500     879/    1500     880/    1500     881/    1500     882/    1500     883/    1500     884/    1500     885/    1500     886/    1500     887/    1500     888/    1500     889/    1500     890/    1500     891/    1500     892/    1500     893/    1500     894/    1500     895/    1500     896/    1500     897/    1500     898/    1500     899/    1500     900/    1500     901/    1500     902/    1500     903/    1500     904/    1500     905/    1500     906/    1500     907/    1500     908/    1500     909/    1500     910/    1500     911/    1500     912/    1500     913/    1500     914/    1500     915/    1500     916/    1500     917/    1500     918/    1500     919/    1500     920/    1500     921/    1500     922/    1500     923/    1500     924/    1500     925/    1500     926/    1500     927/    1500     928/    1500     929/    1500     930/    1500     931/    1500     932/    1500     933/    1500     934/    1500     935/    1500     936/    1500     937/    1500     938/    1500     939/    1500     940/    1500     941/    1500     942/    1500     943/    1500     944/    1500     945/    1500     946/    1500     947/    1500     948/    1500     949/    1500     950/    1500     951/    1500     952/    1500     953/    1500     954/    1500     955/    1500     956/    1500     957/    1500     958/    1500     959/    1500     960/    1500     961/    1500     962/    1500     963/    1500     964/    1500     965/    1500     966/    1500     967/    1500     968/    1500     969/    1500     970/    1500     971/    1500     972/    1500     973/    1500     974/    1500     975/    1500     976/    1500     977/    1500     978/    1500     979/    1500     980/    1500     981/    1500     982/    1500     983/    1500     984/    1500     985/    1500     986/    1500     987/    1500     988/    1500     989/    1500     990/    1500     991/    1500     992/    1500     993/    1500     994/    1500     995/    1500     996/    1500     997/    1500     998/    1500     999/    1500    1000/    1500    1001/    1500    1002/    1500    1003/    1500    1004/    1500    1005/    1500    1006/    1500    1007/    1500    1008/    1500    1009/    1500    1010/    1500    1011/    1500    1012/    1500    1013/    1500    1014/    1500    1015/    1500    1016/    1500    1017/    1500    1018/    1500    1019/    1500    1020/    1500    1021/    1500    1022/    1500    1023/    1500    1024/    1500    1025/    1500    1026/    1500    1027/    1500    1028/    1500    1029/    1500    1030/    1500    1031/    1500    1032/    1500    1033/    1500    1034/    1500    1035/    1500    1036/    1500    1037/    1500    1038/    1500    1039/    1500    1040/    1500    1041/    1500    1042/    1500    1043/    1500    1044/    1500    1045/    1500    1046/    1500    1047/    1500    1048/    1500    1049/    1500    1050/    1500    1051/    1500    1052/    1500    1053/    1500    1054/    1500    1055/    1500    1056/    1500    1057/    1500    1058/    1500    1059/    1500    1060/    1500    1061/    1500    1062/    1500    1063/    1500    1064/    1500    1065/    1500    1066/    1500    1067/    1500    1068/    1500    1069/    1500    1070/    1500    1071/    1500    1072/    1500    1073/    1500    1074/    1500    1075/    1500    1076/    1500    1077/    1500    1078/    1500    1079/    1500    1080/    1500    1081/    1500    1082/    1500    1083/    1500    1084/    1500    1085/    1500    1086/    1500    1087/    1500    1088/    1500    1089/    1500    1090/    1500    1091/    1500    1092/    1500    1093/    1500    1094/    1500    1095/    1500    1096/    1500    1097/    1500    1098/    1500    1099/    1500    1100/    1500    1101/    1500    1102/    1500    1103/    1500    1104/    1500    1105/    1500    1106/    1500    1107/    1500    1108/    1500    1109/    1500    1110/    1500    1111/    1500    1112/    1500    1113/    1500    1114/    1500    1115/    1500    1116/    1500    1117/    1500    1118/    1500    1119/    1500    1120/    1500    1121/    1500    1122/    1500    1123/    1500    1124/    1500    1125/    1500    1126/    1500    1127/    1500    1128/    1500    1129/    1500    1130/    1500    1131/    1500    1132/    1500    1133/    1500    1134/    1500    1135/    1500    1136/    1500    1137/    1500    1138/    1500    1139/    1500    1140/    1500    1141/    1500    1142/    1500    1143/    1500    1144/    1500    1145/    1500    1146/    1500    1147/    1500    1148/    1500    1149/    1500    1150/    1500    1151/    1500    1152/    1500    1153/    1500    1154/    1500    1155/    1500    1156/    1500    1157/    1500    1158/    1500    1159/    1500    1160/    1500    1161/    1500    1162/    1500    1163/    1500    1164/    1500    1165/    1500    1166/    1500    1167/    1500    1168/    1500    1169/    1500    1170/    1500    1171/    1500    1172/    1500    1173/    1500    1174/    1500    1175/    1500    1176/    1500    1177/    1500    1178/    1500    1179/    1500    1180/    1500    1181/    1500    1182/    1500    1183/    1500    1184/    1500    1185/    1500    1186/    1500    1187/    1500    1188/    1500    1189/    1500    1190/    1500    1191/    1500    1192/    1500    1193/    1500    1194/    1500    1195/    1500    1196/    1500    1197/    1500    1198/    1500    1199/    1500    1200/    1500    1201/    1500    1202/    1500    1203/    1500    1204/    1500    1205/    1500    1206/    1500    1207/    1500    1208/    1500    1209/    1500    1210/    1500    1211/    1500    1212/    1500    1213/    1500    1214/    1500    1215/    1500    1216/    1500    1217/    1500    1218/    1500    1219/    1500    1220/    1500    1221/    1500    1222/    1500    1223/    1500    1224/    1500    1225/    1500    1226/    1500    1227/    1500    1228/    1500    1229/    1500    1230/    1500    1231/    1500    1232/    1500    1233/    1500    1234/    1500    1235/    1500    1236/    1500    1237/    1500    1238/    1500    1239/    1500    1240/    1500    1241/    1500    1242/    1500    1243/    1500    1244/    1500    1245/    1500    1246/    1500    1247/    1500    1248/    1500    1249/    1500    1250/    1500    1251/    1500    1252/    1500    1253/    1500    1254/    1500    1255/    1500    1256/    1500    1257/    1500    1258/    1500    1259/    1500    1260/    1500    1261/    1500    1262/    1500    1263/    1500    1264/    1500    1265/    1500    1266/    1500    1267/    1500    1268/    1500    1269/    1500    1270/    1500    1271/    1500    1272/    1500    1273/    1500    1274/    1500    1275/    1500    1276/    1500    1277/    1500    1278/    1500    1279/    1500    1280/    1500    1281/    1500    1282/    1500    1283/    1500    1284/    1500    1285/    1500    1286/    1500    1287/    1500    1288/    1500    1289/    1500    1290/    1500    1291/    1500    1292/    1500    1293/    1500    1294/    1500    1295/    1500    1296/    1500    1297/    1500    1298/    1500    1299/    1500    1300/    1500    1301/    1500    1302/    1500    1303/    1500    1304/    1500    1305/    1500    1306/    1500    1307/    1500    1308/    1500    1309/    1500    1310/    1500    1311/    1500    1312/    1500    1313/    1500    1314/    1500    1315/    1500    1316/    1500    1317/    1500    1318/    1500    1319/    1500    1320/    1500    1321/    1500    1322/    1500    1323/    1500    1324/    1500    1325/    1500    1326/    1500    1327/    1500    1328/    1500    1329/    1500    1330/    1500    1331/    1500    1332/    1500    1333/    1500    1334/    1500    1335/    1500    1336/    1500    1337/    1500    1338/    1500    1339/    1500    1340/    1500    1341/    1500    1342/    1500    1343/    1500    1344/    1500    1345/    1500    1346/    1500    1347/    1500    1348/    1500    1349/    1500    1350/    1500    1351/    1500    1352/    1500    1353/    1500    1354/    1500    1355/    1500    1356/    1500    1357/    1500    1358/    1500    1359/    1500    1360/    1500    1361/    1500    1362/    1500    1363/    1500    1364/    1500    1365/    1500    1366/    1500    1367/    1500    1368/    1500    1369/    1500    1370/    1500    1371/    1500    1372/    1500    1373/    1500    1374/    1500    1375/    1500    1376/    1500    1377/    1500    1378/    1500    1379/    1500    1380/    1500    1381/    1500    1382/    1500    1383/    1500    1384/    1500    1385/    1500    1386/    1500    1387/    1500    1388/    1500    1389/    1500    1390/    1500    1391/    1500    1392/    1500    1393/    1500    1394/    1500    1395/    1500    1396/    1500    1397/    1500    1398/    1500    1399/    1500    1400/    1500    1401/    1500    1402/    1500    1403/    1500    1404/    1500    1405/    1500    1406/    1500    1407/    1500    1408/    1500    1409/    1500    1410/    1500    1411/    1500    1412/    1500    1413/    1500    1414/    1500    1415/    1500    1416/    1500    1417/    1500    1418/    1500    1419/    1500    1420/    1500    1421/    1500    1422/    1500    1423/    1500    1424/    1500    1425/    1500    1426/    1500    1427/    1500    1428/    1500    1429/    1500    1430/    1500    1431/    1500    1432/    1500    1433/    1500    1434/    1500    1435/    1500    1436/    1500    1437/    1500    1438/    1500    1439/    1500    1440/    1500    1441/    1500    1442/    1500    1443/    1500    1444/    1500    1445/    1500    1446/    1500    1447/    1500    1448/    1500    1449/    1500    1450/    1500    1451/    1500    1452/    1500    1453/    1500    1454/    1500    1455/    1500    1456/    1500    1457/    1500    1458/    1500    1459/    1500    1460/    1500    1461/    1500    1462/    1500    1463/    1500    1464/    1500    1465/    1500    1466/    1500    1467/    1500    1468/    1500    1469/    1500    1470/    1500    1471/    1500    1472/    1500    1473/    1500    1474/    1500    1475/    1500    1476/    1500    1477/    1500    1478/    1500    1479/    1500    1480/    1500    1481/    1500    1482/    1500    1483/    1500    1484/    1500    1485/    1500    1486/    1500    1487/    1500    1488/    1500    1489/    1500    1490/    1500    1491/    1500    1492/    1500    1493/    1500    1494/    1500    1495/    1500    1496/    1500    1497/    1500    1498/    1500    1499/    1500

    1500/    1500

Generating estimation report...done.
Discrete-time Neural State-Space Model with 15 outputs, 14 states, and 1 inputs
     x(t+1) = f(x(t),u(t))
     y_1(t) = x(t) + e_1(t)
     y_2(t) = g(x(t),u(t)) + e_2(t)
       y(t) = [y_1(t); y_2(t)]

f(.) network:
  Deep network with 1 fully connected, hidden layers
  Activation function: Sigmoid
g(.) network:
  Deep network with 1 fully connected, hidden layers
  Activation function: Sigmoid

Inputs: Torque
Outputs: Angular Velocity(t-1), Angular Velocity(t-2), Angular Velocity(t-3), Angular Velocity(t-4), Angular Velocity(t-5), Angular Velocity(t-6), Angular Velocity(t-7), Torque(t-1), Torque(t-2), Torque(t-3), Torque(t-4), Torque(t-5), Torque(t-6), Torque(t-7), Angular Velocity
States: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11, x12, x13, x14
Sample time: 0.01 seconds

Status:                                                                                  
Estimated using NLSSEST on time domain data "Data".                                      
Fit to estimation data: [65.19 58.06 63.49 63.41 62.98 65.14 64.52 31.35 12.49 8.173....%
FPE: 2.292e-15, MSE: [6.141 6.324 6.006]                                                 
More information in model's "Report" property.

Model Properties

toc

Elapsed time is 1516.352434 seconds.

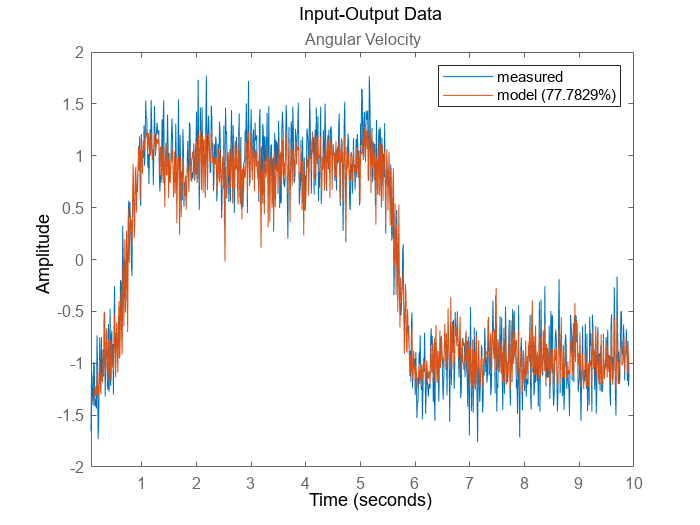
[yp,fit] = compare(XYData, nss);
plot(XYData(:,end,[]),yp(:,end,[]))
legend('measured',['model (',num2str(fit(end)),'%)'])

This estimation takes a long time. For reference, the results are available in the data file IdentifiedNeuralSSModel.mat.

Just like the Hammerstein-Wiener model, a Neural State Space model is an Output Error model. This means that there is no process noise considered as part of the state transition. However, the identified model can be extended post-estimation with a process noise component.

% Simulate the state trajectory
[~,~,Xp] = sim(nss,XYData);
% Fetch measured values of the states
X_measured = XYData.OutputData(:,1:end-1);
% Compute covariace of dX := Xp-X_measured
dX = Xp-X_measured;
XCov = cov(dX); 
NV = nss.NoiseVariance;
Xsd = chol(XCov);
NVc = chol(NV);
NumParticles = 1000;
x0 = X_measured(1,:)'

Use the generateMATLABFunction command to generate MATLAB functions that implement the state-transition and the measurement functions. The functions are generated as M files. An accompanying MAT file is also generated and it must be present together with the M files for the interface to work properly in downstream applications.

Run the following command in a folder with write privileges to generate the Jacobian files nssStateFcn.m, nssMeasurementFcn.m, and the accompanying files.

generateMATLABFunction(nss, "nssStateFcn", "nssMeasurementFcnOutput15");

The generated functions - nssStateFcn and nssMeasurementFcnOutput15 use persistent variables which are not allowed to be used inside MATLAB System blocks (the MATLAB System blocks are used to implement the predictor and corrector functions). Hence we modify these functions, post generation, to remove the use of the persistent variables. The modified functions are called nssStateFcn_2 and nssMeasurementFcnOutput15_2 respectively.

type nssStateFcn_2

function x1 = nssStateFcn(x,u)
%% auto-generated state function of neural state space system
%# codegen
persistent StateNetwork
MATname = 'nssStateFcnData';
if isempty(StateNetwork)
    StateNetwork = coder.load(MATname);
end
out = [x;u];
% hidden layer #1
out = StateNetwork.fc1.Weights*out + StateNetwork.fc1.Bias;
out = deep.internal.coder.sigmoid(out);
% output layer
dx = StateNetwork.output.Weights*out + StateNetwork.output.Bias;
x1 = x + dx;

type nssMeasurementFcnOutput15_2

function y = nssMeasurementFcnOutput15(x,u)
%% auto-generated output function of neural state space system
%# codegen
persistent OutputNetwork
MATname = 'nssMeasurementFcnOutput15Data';
if isempty(OutputNetwork)
    OutputNetwork = coder.load(MATname);
end
out = x;
% hidden layer #1
out = OutputNetwork.fc1.Weights*out + OutputNetwork.fc1.Bias;
out = deep.internal.coder.sigmoid(out);
% output layer
y = OutputNetwork.output.Weights*out + OutputNetwork.output.Bias;

Note that the measurement function file represents only the extra outputs (output numbers nx+1:ny). This is output signal number 15 in XYData. For use in EKF/UKF filters, we need a measurement function that describes all the outputs. Hence we wrap the nssMeasurementFcnOutput15 function in another function called nssMeasurementFcnAllOutputs which appends the model states as its first 14 outputs.

type nssMeasurementFcnAllOutputs

function y = nssMeasurementFcnAllOutputs(x,u)
%% output function of neural state space system
% all outputs
%# codegen

y15 = nssMeasurementFcnOutput15(x,u);
y = [x; y15];

The state-transition function (nssStateFcn.m) and the measurement function (nssMeasurementFcnAllOutputs.m) along with the process noise covariance (XCov) and measurement noise covariance (NV) can be used to set up online state estimators. This is implemented in StateEstimation_Using_NeuralSS.slx.

Ts = nss.Ts;
Ts2 = Ts*10; % correction time interval
open_system('StateEstimation_Using_NeuralSS')

The 10-step ahead prediction results are shown in the 3 scope plots (one for each type of filter), obtained for XYData.

sim('StateEstimation_Using_NeuralSS')

ans = 
  Simulink.SimulationOutput:

                   tout: [99101x1 double] 

     SimulationMetadata: [1x1 Simulink.SimulationMetadata] 
           ErrorMessage: [0x0 char]

Nonlinear Grey Box Model

Finally, we explore the modeling approach that requires the maximum amount of physical knowledge regarding the dynamics. This results in a 5th order nonlinear differential equation. In state-space form these equations are:

$\begin{array}{l} State defintion : \\ x_{1} (t) = q_{m} (t) - q_{g} (t) \\ x_{2} (t) = q_{g} (t) - q_{a} (t) \\ x_{3} (t) = {\dot{q}}_{m} (t) \\ x_{4} (t) = {\dot{q}}_{g} (t) \\ x_{5} (t) = {\dot{q}}_{a} (t) \end{array}$

$\begin{array}{l} Equations of motion : \\ {\dot{x}}_{1} (t) = x_{3} (t) - x_{4} (t) \\ {\dot{x}}_{2} (t) = x_{4} (t) - x_{5} (t) \\ {\dot{x}}_{3} (t) = \frac{1}{J_{m}} (- τ_{s} (t) - d_{g} (x_{3} (t) - x_{4} (t)) - τ_{f} (t) + u (t)) \\ {\dot{x}}_{4} (t) = \frac{1}{J_{g}} (τ_{s} (t) + d_{g} (x_{3} (t) - x_{4} (t)) - k_{a} x_{2} (t) - d_{a} (x_{4} (t) - x_{5} (t))) \\ {\dot{x}}_{5} (t) = \frac{1}{J_{a}} (k_{a} x_{2} (t) + d_{a} (x_{4} (t) - x_{5} (t))) \\ y (t) = x_{3} (t) \end{array}$

where:

$J_{m} . J_{g}, J_{a}$ are the moments of inertia of the motor, the gear-box and the arm structure, respectively
$d_{g}, d_{a}$ are damping parameters
$k_{a}$ is the stiffness of the arm structure.
The gear-box friction torque $τ_{f} (t) = F_{v} x_{3} (t) + (F_{c} + F_{cs} sech (α x_{3} (t))) \tanh (β x_{3} (t))$ , where $F_{v}$ and $F_{c}$ are the viscous and the Coulomb friction coefficients, $F_{cs}$ and $α$ are coefficients for reflecting the Stribeck effect, and $β$ is a parameter used to obtain a smooth transition from negative to positive velocities of $x_{3} (t)$ .
The torque of the spring $τ_{s} (t) = k_{g1} x_{1} (t) + k_{g3} x_{1}^{3} (t)$ , where $k_{g1}, k_{g3}$ are stiffness parameters of the gear-box spring.

The equations can be described by a Nonlinear Grey Box model (the idnlgrey object). The model structure for a nonlinear grey-box model is:

$\begin{array}{l} \dot{x} (t) = f (t, x, u, θ) \\ y (t) = g (t, x, u, θ) + e (t) \end{array}$

where $θ$ denotes the set of parameters used in the functions $f (.), g (.)$ . The identification task is to estimate $θ$ in order to minimize the difference between the simulated response of the model and its measured value. The procedure is similar to the one described above for the linear grey box case - the main task is to write an ODE file that returns the state derivatives $\dot{x} (t)$ , and output $y (t)$ as a function of $t, u (t), x (t)$ and the parameters. This exercise is the focus of the example "Modeling an Industrial Robot Arm". For current purposes, load the estimation results from this example.

load RobotArmNonlinearGreyBoxModel nlgr
nlgr.Name = 'Original Model (no process noise)';
nlgr

nlgr =

Continuous-time nonlinear grey-box model defined by 'robotarm_c' (MEX-file):

   dx/dt = F(t, u(t), x(t), p1, ..., p13)
    y(t) = H(t, u(t), x(t), p1, ..., p13) + e(t)

 with 1 input(s), 5 state(s), 1 output(s), and 7 free parameter(s) (out of 13).

Name: Original Model (no process noise)

Status:                                                                                
Estimated using Solver: ode45; Search: lsqnonlin on time domain data "estimation data".
Fit to estimation data: 85.52%                                                         
FPE: 9.184, MSE: 9.092                                                                 

Model Properties

compare(vData, nlgr)

Similar to the linear case, you can embed the identified nonlinear grey box model into a more general stochastic framework by adding process noise to the equations for $\dot{x} (t)$ , that is, pose $\dot{x} (t) = f (t, x, u, θ) + Gw (t)$ , where $G$ is the process noise gain matrix. However, there is no direct way to compute the value of $G$ under the nonlinear grey-box estimation framework. This is because the Nonlinear Grey Box methodology only handles Output-Error models, that is, it does not consider the influence of process noise.

An option is to pose a simple extension $\dot{x} (t) = f (t, x, u, θ) + Ke (t)$ , where $e (t)$ is the output prediction error. This is similar to the innovations form of the linear state-space model, where $\dot{x} (t) = Ax (t) + Bu (t) + Ke (t)$

For prediction of model output, the nonlinear predictor therefore takes the form:

$\begin{array}{l} {\dot{x}}_{p} (t) = f (t, x, u, θ) + K (y_{measured} - y_{p} (t)) \\ y_{p} (t) = g (t, x, u, θ) \end{array}$

In order to make this extension, add $K$ as a free parameter (5x1 vector) to the model nlgr. Also, the ODE function needs to compute $y_{measured} - y_{p} (t)$ . Replace the original ODE function employed by nlgr (robot_c) with a new one called robotARMNonlinearODE. For this, pass a gridded interpolator as a function argument.

type robotARMNonlinearODE

function [dx, y] = robotARMNonlinearODE(t, x, u, Fv, Fc, Fcs, alpha, beta, J, am, ...
   ag, kg1, kg3, dg, ka, da, K, Interpolator)
%robotARMNonlinearODE A physically parameterized robot arm.
% t: time instant (seconds)
% x: state value at time t (5 x 1 vector)
% u: input at time t (scalar)
% Fv, Fc, Fcs, alpha, beta, J, am, ag, kg1, kg3, dg, ka, da: parameters related to the model
% dynamics
% K: process noise gain matrix (free parameter)
% Interpolator: griddedInterpolant object to fetch measured output at a time t

%   Copyright 2005-2022 The MathWorks, Inc.

% Output equation.
y = x(3);                                                   % Rotational velocity of the motor.

% Intermediate quantities (gear box).
tauf = Fv*x(3)+(Fc+Fcs/cosh(alpha*x(3)))*tanh(beta*x(3));   % Gear friction torque.
taus = kg1*x(1)+kg3*x(1)^3;                                 % Spring torque.

% State equations.
dx = [x(3)-x(4);       ... % Rotational velocity difference between the motor and the gear-box.
   x(4)-x(5);       ... % Rotational velocity difference between the gear-box and the arm.
   1/(J*am)*(-taus-dg*(x(3)-x(4))-tauf+u);                ... % Rotational velocity of the motor.
   1/(J*ag)*(taus+dg*(x(3)-x(4))-ka*x(2)-da*(x(4)-x(5))); ... % Rotational velocity after the gear-box.
   1/(J*(1-am-ag))*(ka*x(2)+da*(x(4)-x(5)))               ... % Rotational velocity of the robot arm.
   ];

ym = Interpolator{1}(t);
dx = dx + K*(ym-y);

The last line of code adds a correction term to the state derivatives based on the output prediction error. In order to compute the measured output value at a given time instant, we can simply interpolate the values in eData.OutputData. To enable this, we pass a gridded interpolant as an extra input argument to the ODE function (see the last input argument "Interpolator"). When setting up the nonlinear grey-box model (idnlgrey object), you can specify any extra arguments to the ODE function using the FileArgument property.

% Change the ODE function of nlgr from "motor_c" to "robotARMNonlinearODE". robotARMNonlinearODE is
% mostly identical to motor_c except for the addition of the correction to dx induced by the process
% noise.   
PredictorModel = nlgr;
PredictorModel.Name = 'Predictor form';
PredictorModel.FileName = 'robotARMNonlinearODE';

% Create a new parameter to represent the process noise gain K
% Set 0 as initial guess for K entries
NoiseGain = struct('Name','K','Unit','','Value',zeros(5,1),...
   'Minimum',-Inf(5,1),'Maximum',Inf(5,1),'Fixed',false(5,1));

% Add this parameter to the model
PredictorModel.Parameters(end+1) = NoiseGain;

% Create a linear interpolator
t = eData.SamplingInstants;
y = eData.OutputData; % measured output
Interpolator = griddedInterpolant(t,y);
Interpolator.ExtrapolationMethod = 'nearest';
PredictorModel.FileArgument = {Interpolator};

Perform parameter estimation, Because of the process noise correction, the estimation is implicitly minimizing the 1-step ahead prediction error (rather than the default behavior which is to minimize the simulation error)

opt = nlgreyestOptions('Display', 'on','SearchMethod','lm');
opt.SearchOptions.MaxIterations = 20;
opt.EstimateCovariance = false; % to speed up estimation
% Keep the parameter estimates close to their initial guesses. This is because we already have a
% good guess of their values from previous estimation as carried out in the example "Modeling an
% Industrial Robot Arm"
opt.Regularization.Lambda = .1;
opt.Regularization.Nominal = 'model';

% Estimate the model parameters
PredictorModel = nlgreyest(eData, PredictorModel, opt)

PredictorModel =

Continuous-time nonlinear grey-box model defined by 'robotARMNonlinearODE' (MATLAB file):

   dx/dt = F(t, u(t), x(t), p1, ..., p14, FileArgument)
    y(t) = H(t, u(t), x(t), p1, ..., p14, FileArgument) + e(t)

 with 1 input(s), 5 state(s), 1 output(s), and 12 free parameter(s) (out of 18).

Name: Predictor form

Status:                                                                         
Estimated using Solver: ode45; Search: lm on time domain data "estimation data".
Fit to estimation data: 90.87%                                                  
FPE: 3.674, MSE: 3.618                                                          

Model Properties

compare(eData, nlgr, PredictorModel)

% Fetch the computed process noise gain matrix
K = PredictorModel.Parameters(end).Value

% Fetch the output noise variance
NV = PredictorModel.NoiseVariance

NV = 0.0182

Validate the model.

% Check 1-step ahead prediction quality on validation dataset
tv = vData.SamplingInstants;
yv = vData.OutputData; % measured output
Interpolator2 = griddedInterpolant(tv,yv);
Interpolator2.ExtrapolationMethod = 'nearest';
PredictorModel.FileArgument = {Interpolator2};
compare(vData, nlgr, PredictorModel)

As seen from both the comparisons to the training data (eData) as well as the validation data (vData), the correction applied to the state-transition using the noise gain K has a beneficial effect on 1-step ahead predictions. Note that the original model (nlgr) has no process noise component. Hence for this model, 1-step ahead prediction is same as pure simulation.

You now have all the information available to implement nonlinear state estimators. Use the functions $f (.), g (.)$ , as implemented in robotARMNonlinearODE to specify the state transition and measurement functions for the filters. The process noise is zero-mean Gaussian with a variance equal to $E {{ww}^{'}} = K Σ K^{T}$ , where $Σ$ =NV is the measurement covariance.

10-Step Ahead Prediction

Compute 10-step ahead prediction of the vData output using EKF, UKF, and PF state estimators based on PredictorModel.

% Gather block data
Ts = eData.Ts; % prediction interval
Ts2 = 10*Ts; % correction interval
% Parameter variables for use in the filter blocks
[Fv, Fc, Fcs, alpha, beta, J, am, ag, kg1, kg3, dg, ka, da, K] = deal(PredictorModel.Parameters.Value);
NumParticles = 1000; % number of particles used by the Particle filter

open_system('StateEstimation_Using_NonlinearGreyBox')

The Simulink model is set up to use a fixed step discrete solver with a fixed-step size of Ts/100 = 50 ms. The state transition equation used by the filters is implemented in the nlgreyPredictFcn function. This model is setup in a manner very similar to the one for Nonlinear ARX model based state prediction (see StateEstimation_Using_NonlinearARX.slx)

type nlgreyPredictFcn

function xnext = nlgreyPredictFcn(x,u,Fv, Fc, Fcs, alpha, beta, J, am, ...
   ag, kg1, kg3, dg, ka, da, Ts)
% Predict the state update for the nonlinear grey box model of robot arm.
% State transition function for the UKF/EKF block.
% Ts: data sample time. The model has been configured to use a fixed step size of Ts/100.

%  Copyright 2022 The MathWorks, Inc.

% Euler integration of continuous-time dynamics x'=f(x) with sample time dt
xnext = x;
for i = 1:size(x,2)
   xnext(:,i) = x(:,i) + continuousTimeDerivative(x(:,i),u,...
      Fv,Fc,Fcs,alpha,beta,J,am,ag,kg1,kg3,dg,ka,da)*Ts/100;
end
end

%---------------------------------------------------------------------------------------------------
function dx = continuousTimeDerivative(x,u,Fv, Fc, Fcs, alpha, beta, J, am, ...
   ag, kg1, kg3, dg, ka, da)
% Robot arm state derivatives.

tauf = Fv*x(3)+(Fc+Fcs/cosh(alpha*x(3)))*tanh(beta*x(3));   % Gear friction torque.
taus = kg1*x(1)+kg3*x(1)^3;                                 % Spring torque.

% State equations.
dx = [x(3)-x(4);       ... % Rotational velocity difference between the motor and the gear-box.
   x(4)-x(5);       ... % Rotational velocity difference between the gear-box and the arm.
   1/(J*am)*(-taus-dg*(x(3)-x(4))-tauf+u);                ... % Rotational velocity of the motor.
   1/(J*ag)*(taus+dg*(x(3)-x(4))-ka*x(2)-da*(x(4)-x(5))); ... % Rotational velocity after the gear-box.
   1/(J*(1-am-ag))*(ka*x(2)+da*(x(4)-x(5)))               ... % Rotational velocity of the robot arm.
   ];
end

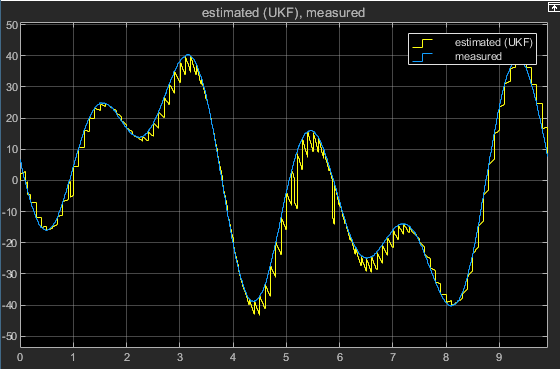
The 10-step ahead prediction results are shown in the 3 scope plots (one for each type of filter)

sim('StateEstimation_Using_NonlinearGreyBox');