使用盲反卷积算法对图像进行去模糊

步骤 1：读取图像

将灰度图像读入工作区。deconvblind 函数可以处理任何维度的数组。

I = imread("cameraman.tif");
imshow(I)
title("Original Image")

步骤 2：仿真模糊效果

模拟模糊的真实图像（例如，因为相机移动或失焦而模糊）。此示例通过使用高斯滤波器对真实图像进行卷积来模拟模糊效果（使用 imfilter）。然后，高斯滤波器表示点扩散函数 PSF。

PSF = fspecial("gaussian",7,10);
Blurred = imfilter(I,PSF,"symmetric","conv");
imshow(Blurred)
title("Blurred Image")

步骤 3：使用不同大小的 PSF 还原模糊图像

为了说明了解真实 PSF 大小的重要性，此示例执行三次还原。对于每次还原，PSF 重构都从均匀数组（全一数组）开始。

第一次还原由 J1 和 P1 描述，使用大小过小的数组 UNDERPSF 获得 PSF 的初始估计值。在每个维度上，UNDERPSF 数组的大小都比真实 PSF 短 4 个像素。

UNDERPSF = ones(size(PSF)-4);
[J1,P1] = deconvblind(Blurred,UNDERPSF);
imshow(J1)
title("Deblurring with Undersized PSF")

第二次还原由（J2 和 P2）说明，使用全一数组 OVERPSF 来获得初始 PSF，该初始 PSF 在每个维度上都比真实 PSF 长 4 个像素。

OVERPSF = padarray(UNDERPSF,[4 4],"replicate","both");
[J2,P2] = deconvblind(Blurred,OVERPSF);
imshow(J2)
title("Deblurring with Oversized PSF")

第三次还原由（J3 和 P3）说明，使用全一数组 INITPSF 获得与真实 PSF 大小完全相同的初始 PSF。

INITPSF = padarray(UNDERPSF,[2 2],"replicate","both");
[J3,P3] = deconvblind(Blurred,INITPSF);
imshow(J3)
title("Deblurring with INITPSF")

步骤 4：分析还原的 PSF

所有三个还原还会生成一个 PSF。下列各图显示对重构的 PSF 的分析如何有助于估计初始 PSF 的正确大小。在真实的 PSF（一个高斯滤波器）中，最大值在中心（白色），在边界处（黑色）减小。

subplot(2,2,1)
imshow(PSF,[],InitialMagnification="fit")
title("True PSF")
subplot(222)
imshow(P1,[],InitialMagnification="fit")
title("Reconstructed Undersized PSF")
subplot(2,2,3)
imshow(P2,[],InitialMagnification="fit")
title("Reconstructed Oversized PSF")
subplot(2,2,4)
imshow(P3,[],InitialMagnification="fit")
title("Reconstructed true PSF")

在第一次还原中重构的 PSF P1 显然无法放入限定的大小之内。它在边界上有很强的信号变化。相对于模糊图像 Blurred，对应的图像 J1 在清晰度上并未显示出任何改进。

在第二个还原中重构的 PSF (P2) 在边缘处非常平滑。这意味着还原可以处理大小较小的 PSF。对应的图像 J2 显示消除了一些模糊，但被振铃效应严破坏。

最后，在第三个还原中重构的 PSF P3 介于 P1 和 P2 之间。数组 P3 非常像真实的 PSF。对应的图像 J3 显示出显著的改进；然而，它仍然被振铃效应破坏。

步骤 5：改进还原

还原的图像 J3 中的振铃效应发生在强度对比强烈的区域和图像边界上。此示例说明如何通过指定加权函数来减少振铃效应。该算法根据 WEIGHT 数组对每个像素进行加权，同时还原图像和 PSF。在我们的示例中，我们首先使用边缘函数找到“较高锐度”的像素。通过反复试验，我们确定理想的阈值水平是 0.08。

WEIGHT = edge(Blurred,"sobel",0.08);

要加宽区域，请使用 imdilate 并传入盘形结构元素 se。

se = strel("disk",2);
WEIGHT = 1-double(imdilate(WEIGHT,se));

靠近边界的像素也被赋值为 0。

WEIGHT([1:3 end-(0:2)],:) = 0;
WEIGHT(:,[1:3 end-(0:2)]) = 0;
imshow(WEIGHT)
title("Weight Array")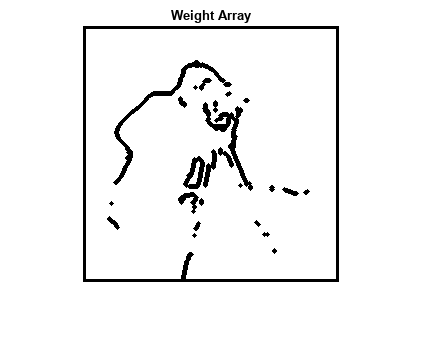

通过使用 WEIGHT 数组和增加的迭代次数 (30) 调用 deconvblind 来还原图像。几乎所有振铃效应都被消除。

[J,P] = deconvblind(Blurred,INITPSF,30,[],WEIGHT);
imshow(J)
title("Deblurred Image")

步骤 6：对 PSF 还原使用附加约束

此示例说明如何对 PSF 指定附加约束。以下函数 FUN 返回修正 PSF 数组，deconvblind将该数组用于下一次迭代。

在此示例中，FUN 会修正 PSF，分别在每个维度中裁去 P1 和 P2 个像素，然后用零回填数组以恢复其原始大小。此运算不会更改 PSF 中心的值，但实际上会将 PSF 大小减小 2*P1 和 2*P2 个像素。

P1 = 2;
P2 = 2;
FUN = @(PSF) padarray(PSF(P1+1:end-P1,P2+1:end-P2),[P1 P2]);

匿名函数 FUN 最后会传入 deconvblind 中。有关为函数 FUN 提供附加参数的详细信息，请参阅参数化函数。

在此示例中，初始 PSF OVERPSF 的大小比真实 PSF 大 4 个像素。将 P1 = 2 和 P2 = 2 设置为 FUN 中的参数，实际上是使 OVERPSF 中的有效空间与真实的 PSF 大小相同。因此，结果（JF 和 PF）与步骤 4 中的结果 J 和 P 类似，该步骤中执行卷积时使用了合适大小的 PSF，但没用调用 FUN。

[JF,PF] = deconvblind(Blurred,OVERPSF,30,[],WEIGHT,FUN);
imshow(JF)
title("Deblurred Image")

如果我们使用了过大的初始 PSF OVERPSF 而没有使用约束函数 FUN，得到的图像将类似于在步骤 3 中获得的不尽如人意的结果 J2。

请注意，在 FUN 之前的任何未指定参数都可以直接省略，例如此示例中的 DAMPAR 和 READOUT，不需要补上占位符 ([])。