Radon Transform

Note

For information about creating projection data from line integrals along paths that radiate from a single source, called fan-beam projections, see Fan-Beam Projection. To convert parallel-beam projection data to fan-beam projection data, use the para2fan function.

The radon function computes projections of an image matrix along specified directions.

A projection of a two-dimensional function f(x,y) is a set of line integrals. The radon function computes the line integrals from multiple sources along parallel paths, or beams, in a certain direction. The beams are spaced 1 pixel unit apart. To represent an image, the radon function takes multiple, parallel-beam projections of the image from different angles by rotating the source around the center of the image. 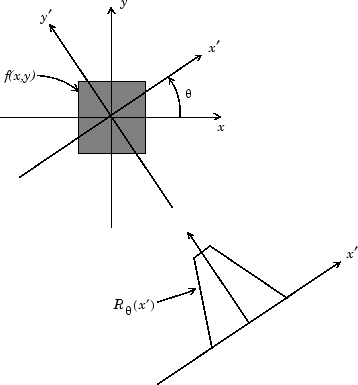The following figure shows a single projection at a specified rotation angle.

Parallel-Beam Projection at Rotation Angle Theta

Single projection of parallel beams at a rotation angle of theta about the center of the coordinate system.

For example, the line integral of f(x,y) in the vertical direction is the projection of f(x,y) onto the x-axis; the line integral in the horizontal direction is the projection of f(x,y) onto the y-axis. The following figure shows horizontal and vertical projections for a simple two-dimensional function.

Horizontal and Vertical Projections of a Simple Function

For a 2-D rectangular object aligned with the x and y axes, the horizontal and vertical projections are 1-D box functions with the same vertical and horizontal spatial extents as the rectangle, respectively.

Projections can be computed along any angle theta (θ). In general, the Radon transform of f(x,y) is the line integral of f parallel to the y´-axis

$R_{θ} (x') = \int_{- \infty}^{\infty} f (x' \cos θ - y' \sin θ, x' \sin θ + y' \cos θ) d y'$

where

$[\begin{matrix} x' \\ y' \end{matrix}] = [\begin{matrix} \cos θ & sin θ \\ - \sin θ & cos θ \end{matrix}] [\begin{matrix} x \\ y \end{matrix}]$

The following figure illustrates the geometry of the Radon transform.

Geometry of the Radon Transform

The Radon transform of a square at an arbitrary projection angle is an isosceles trapezoid whose axis of symmetry is the y'-axis.

Plot the Radon Transform of an Image

Open Live Script

This example shows how to compute the Radon transform of an image for a specific set of rotations angles using the radon function.

Create a small sample image that consists of a single square object, and display the image.

I = zeros(100,100);
I(25:75,25:75) = 1;
imshow(I)

Figure contains an axes object. The hidden axes object contains an object of type image.

Calculate the Radon transform of the image for the angles 0° and 30°. The function returns, R, in which the columns contain the Radon transform for each angle in theta. The function also returns the vector, xp, which contains the corresponding coordinates along the x-axis. The center pixel of I is defined to be floor((size(I)+1)/2), which is the pixel on the x-axis corresponding to x' = 0.

theta = [0 30];
[R,xp] = radon(I,theta);

Plot the transform at 0°.

figure
plot(xp,R(:,1))
title("Radon Transform of Square Function at 0 Degrees")

Figure contains an axes object. The axes object with title Radon Transform of Square Function at 0 Degrees contains an object of type line.

Plot the transform at 30°.

plot(xp,R(:,2));
title("Radon Transform of Square Function at 30 Degrees")

Figure contains an axes object. The axes object with title Radon Transform of Square Function at 30 Degrees contains an object of type line.

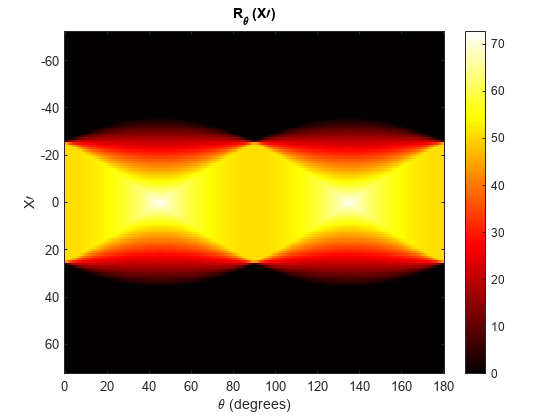
The Radon transform is often calculated for a large number of angles and displayed as an image. Calculate the Radon transform for the square image at angles from 0° to 180°, in 1° increments.

theta = 0:180;
[R,xp] = radon(I,theta);

Display the 2-D Radon transform as a sinogram.

figure
imagesc(theta,xp,R)
title("R_{\theta} (X\prime)")
xlabel("\theta (degrees)")
ylabel("X\prime")
set(gca,"XTick",0:20:180)
colormap(hot)
colorbar

Figure contains an axes object. The axes object with title R indexOf theta baseline blank (X prime ), xlabel theta blank (degrees), ylabel X prime contains an object of type image.