Register Multimodal MRI Images

Step 1: Load Images

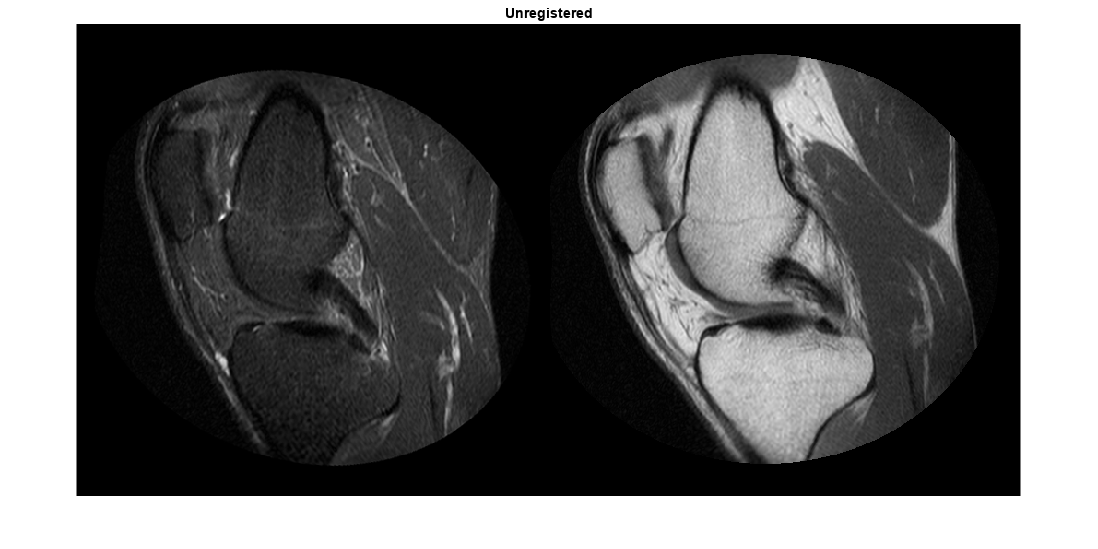
This example uses two MRI images of a knee. The fixed image is a spin echo image, while the moving image is a spin echo image with inversion recovery. The two sagittal slices were acquired at the same time but are slightly out of alignment.

fixed = dicomread("knee1.dcm");
moving = dicomread("knee2.dcm");

The imshowpair function is useful to visualize images during every part of the registration process. Use it to see the two images individually in a montage or display them overlapping to show the amount of misregistration.

imshowpair(moving,fixed,"montage")
title("Unregistered")

In the overlapping image from imshowpair, gray areas correspond to areas that have similar intensities, while magenta and green areas show places where one image is brighter than the other. In some image pairs, green and magenta areas do not always indicate misregistration, but in this example it is easy to use the color information to see where they do.

imshowpair(moving,fixed)
title("Unregistered")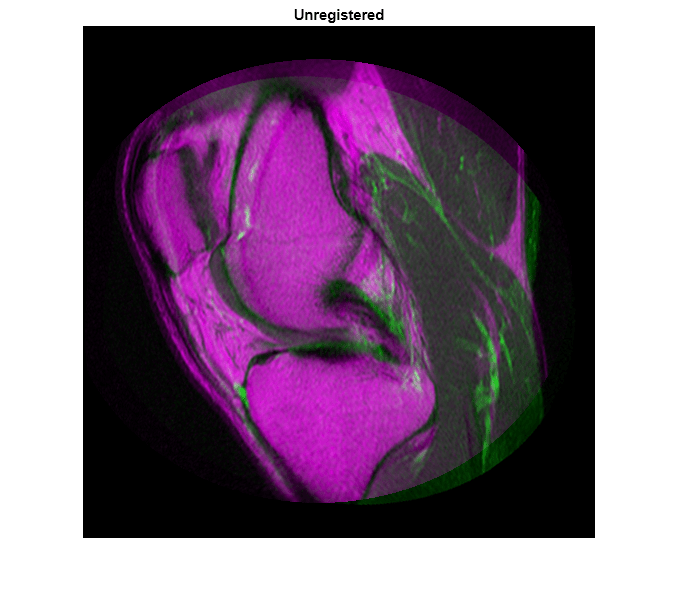

Step 2: Set up the Initial Registration

The imregconfig function makes it easy to pick the correct optimizer and metric configuration to use with imregister. The optimizer and metric variables are objects whose properties control the registration. For more information, see Create an Optimizer and Metric for Intensity-Based Image Registration.

These two images have different intensity distributions, which suggests a multimodal configuration.

[optimizer,metric] = imregconfig("multimodal");

The distortion between the two images includes scaling, rotation, and possibly shear. Use an affine transformation to register the images.

registeredDefault = imregister(moving,fixed,"affine",optimizer,metric);

Display the result. It is very rare that imregister will align images perfectly with the default settings. Nevertheless, using them is a useful way to decide which properties to tune first.

imshowpair(registeredDefault,fixed)
title("A: Default Registration")

Step 3: Improve Registration by Tuning Optimizer and Metric

The initial registration is not very good. There are still significant regions of poor alignment, particularly along the right edge. Try to improve the registration by adjusting the optimizer and metric configuration properties.

disp(optimizer)

  registration.optimizer.OnePlusOneEvolutionary

  Properties:
         GrowthFactor: 1.050000e+00
              Epsilon: 1.500000e-06
        InitialRadius: 6.250000e-03
    MaximumIterations: 100

disp(metric)

  registration.metric.MattesMutualInformation

  Properties:
    NumberOfSpatialSamples: 500
     NumberOfHistogramBins: 50
              UseAllPixels: 1

The InitialRadius property of the optimizer controls the initial step size used in parameter space to refine the geometric transformation. When multimodal registration problems do not converge with the default parameters, InitialRadius is a good first parameter to adjust. Start by reducing the default value of InitialRadius by a scale factor of 3.5.

optimizer.InitialRadius = optimizer.InitialRadius/3.5;
registeredAdjustedInitialRadius = imregister(moving,fixed,"affine",optimizer,metric);

Display the result. Adjusting InitialRadius has a positive impact. There is a noticeable improvement in the alignment of the images at the top and right edges.

imshowpair(registeredAdjustedInitialRadius,fixed)
title("B: Adjusted InitialRadius")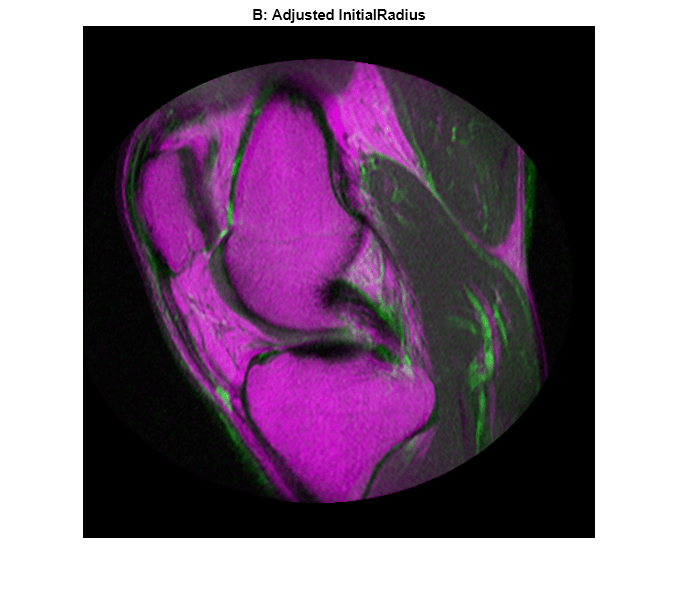

The MaximumIterations property of the optimizer controls the maximum number of iterations that the optimizer will be allowed to take. Increasing MaximumIterations allows the registration search to run longer and potentially find better registration results. Does the registration continue to improve if the InitialRadius from the last step is used with a large number of iterations?

optimizer.MaximumIterations = 300;
registeredAdjustedInitialRadius300 = imregister(moving,fixed,"affine",optimizer,metric);

Display the results. Further improvement in registration was achieved by reusing the InitialRadius optimizer setting from the previous registration and allowing the optimizer to take a large number of iterations.

imshowpair(registeredAdjustedInitialRadius300,fixed)
title("C: Adjusted InitialRadius, MaximumIterations = 300")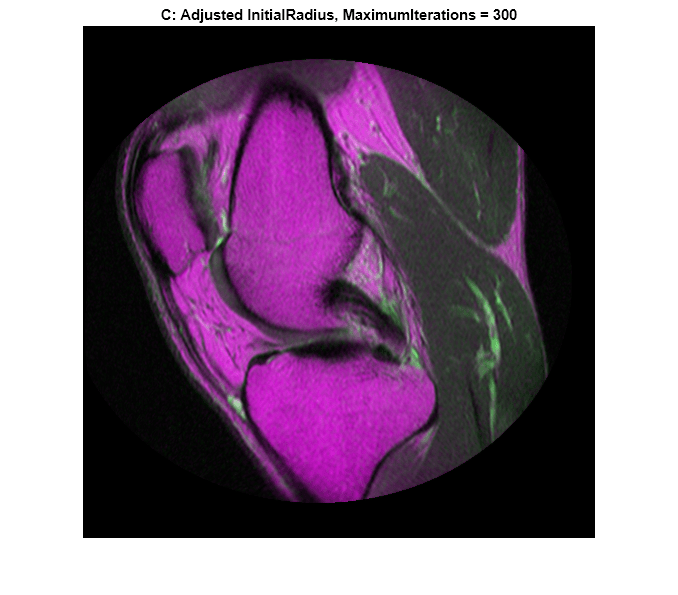

Step 4: Improve Registration Using Initial Conditions

Optimization based registration works best when a good initial condition can be given for the registration that relates the moving and fixed images. A useful technique for getting improved registration results is to start with more simple transformation types such as rigid or similarity transformations, and then to use the resulting transformation as an initial condition for more complicated affine transformation types.

The function imregtform uses the same algorithm as imregister, but returns a geometric transformation object as output instead of a registered output image. Use imregtform to get an initial transformation estimate based on a similarity transformation consisting of translation, rotation, and isotropic scaling. Use the tuned optimizer settings.

tformSimilarity = imregtform(moving,fixed,"similarity",optimizer,metric)

tformSimilarity = 
  simtform2d with properties:

    Dimensionality: 2
             Scale: 1.0390
     RotationAngle: -6.1345
       Translation: [-51.1491 6.9891]
                 R: [2x2 double]

                 A: [ 1.0331    0.1110  -51.1491
                     -0.1110    1.0331    6.9891
                           0         0    1.0000]

Because the registration is being solved in the default coordinate system, also known as the intrinsic coordinate system, obtain the default spatial referencing object that defines the location and resolution of the fixed image.

Rfixed = imref2d(size(fixed));

Use imwarp to apply the geometric transformation output from imregtform to the moving image to align it with the fixed image. Use the OutputView name-value argument in imwarp to assign to the moving image the same resolution and world limits as the fixed image.

registeredSimilarity = imwarp(moving,tformSimilarity,OutputView=Rfixed);

Display the result.

imshowpair(registeredSimilarity,fixed)
title("D: Registration Based on Similarity Transformation Model")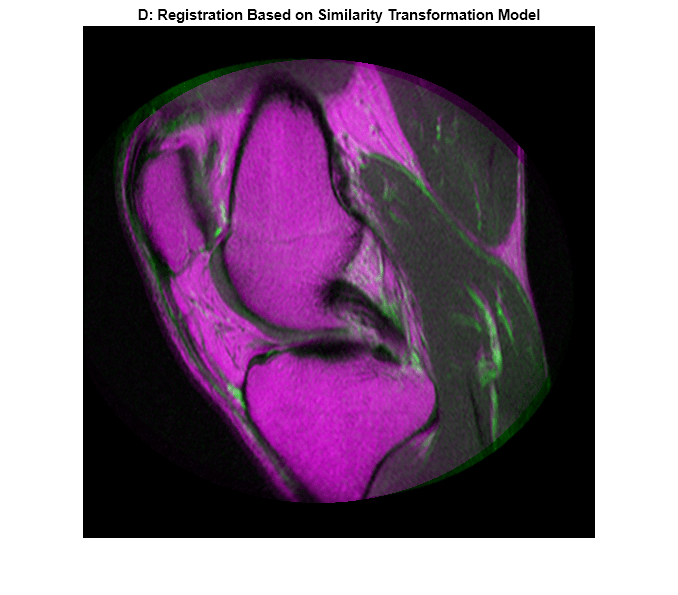

Refine the registration by using an affine transformation model and specifying the similarity transformation as the initial condition. The refined estimate for the registration includes the possibility of shear.

registeredAffineWithIC = imregister(moving,fixed,"affine",optimizer,metric, ...
    InitialTransformation=tformSimilarity);

Display the result. Refining the registration with a similarity initial condition yields a nice registration result.

imshowpair(registeredAffineWithIC,fixed)
title("E: Registration from Affine Model Based on Similarity Initial Condition")

Step 5: Decide When Enough is Enough

Comparing the results of running imregister with different configurations and initial conditions, it becomes apparent that there are a large number of input parameters that can be varied in imregister, each of which may lead to different registration results.

It can be difficult to quantitatively compare registration results because there is no one quality metric that accurately describes the alignment of two images. Often, registration results must be judged qualitatively by visualizing the results. In the results above, the registration results in C) and E) are both very good and are difficult to tell apart visually.

Step 6: Alternate Visualizations

Often as the quality of multimodal registrations improve it becomes more difficult to judge the quality of registration visually. This is because the intensity differences can obscure areas of misalignment. Sometimes switching to a different display mode for imshowpair exposes hidden details. (This is not always the case.)