Quantify Map Distortions at Point Locations

The tissot and mdistort functions provide synoptic visual overviews of different forms of map projection error. Sometimes, however, you need numerical estimates of error at specific locations in order to quantify or correct for map distortions. This is useful, for example, if you are sampling environmental data on a uniform basis across a map, and want to know precisely how much area is associated with each sample point, a statistic that will vary by location and be projection dependent. Once you have this information, you can adjust environmental density and other statistics you collect for areal variations induced by the map projection.

A Mapping Toolbox™ function returns location-specific map error statistics from the current projection or an mstruct. The distortcalc function computes the same distortion statistics as mdistort does, but for specified locations provided as arguments. You provide the latitude-longitude locations one at a time or in vectors. The general form is

[areascale,angdef,maxscale,minscale,merscale,parscale] = ...
    distortcalc(mstruct,lat,long)

However, if you are evaluating the current map figure, omit the mstruct. You need not specify any return values following the last one of interest to you.

Use `distortcalc` to Determine Map Projection Geometric Distortions

The following exercise uses distortcalc to compute the maximum area distortion for a map of Argentina from the land areas data set.

Read the North and South America polygon:

Americas = shaperead('landareas.shp','UseGeoCoords',true, ...
    'Selector', {@(name) ...
    strcmpi(name,{'north and south america'}),'Name'});

Set the spatial extent (map limits) to contain the southern part of South America and also include an area closer to the South Pole:
```
mlatlim = [-72.0 -20.0];
mlonlim = [-75.0 -50.0];
[alat, alon] = maptriml([Americas.Lat], ...
    [Americas.Lon], mlatlim, mlonlim);
```
Create a Mercator cylindrical conformal projection using these limits, specify a five-degree graticule, and then plot the outline for reference:
```
figure;
axesm('MapProjection','mercator','grid','on', ...
    'MapLatLimit',mlatlim,'MapLonLimit',mlonlim,...
    'MLineLocation',5, 'PLineLocation',5)
plotm(alat,alon,'b')
```
The map looks like this:
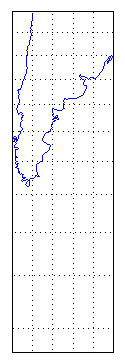
Sample every tenth point of the patch outline for analysis:
```
alats = alat(1:10:numel(alat));
alons = alon(1:10:numel(alat));
```
Compute the area distortions (the first value returned by distortcalc) at the sample points:
```
adistort = distortcalc(alats, alons);
```
Find the range of area distortion across Argentina (percent of a unit area on, in this case, the equator):
```
adistortmm = [min(adistort) max(adistort)]

adistortmm =
    1.1790    2.7716
```
As Argentina occupies mid southern latitudes, its area on a Mercator map is overstated, and the errors vary noticeably from north to south.
Remove any NaNs from the coordinate arrays and plot symbols to represent the relative distortions as proportional circles, using scatterm:
```
nanIndex = isnan(adistort);
alats(nanIndex) = [];
alons(nanIndex) = [];
adistort(nanIndex)  = [];
scatterm(alats,alons,20*adistort,'red','filled')
```
The resulting map is shown below:
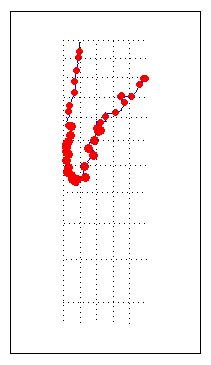
The degree of area overstatement would be considerably larger if it extended farther toward the pole. To see how much larger, get the area distortion for 50°S, 60°S, and 70°S:
```
a=distortcalc(-50,-60)

a =
       2.4203

a=distortcalc(-60,-60)

a =
            4

>> a=distortcalc(-70,-60)

a =
       8.5485
```
Note
You can only use distortcalc to query locations that are within the current map frame or mstruct limits. Outside points yield NaN as a result.
Using this technique, you can write a simple script that lets you query a map repeatedly to determine distortion at any desired location. You can select locations with the graphic cursor using inputm. For example,
```
[plat plon] = inputm(1)

plat =
      -62.225
plon =
      -72.301
>> a=distortcalc(plat,plon)

a =
       4.6048
```
Naturally the answer you get will vary depending on what point you pick. Using this technique, you can write a simple script that lets you query a map repeatedly to determine any distortion statistic at any desired location.

Try changing the map projection or even the orientation vector to see how the choice of projection affects map distortion. For further information, see the reference page for distortcalc.

Quantify Map Distortions at Point Locations

Use distortcalc to Determine Map Projection Geometric Distortions

Use `distortcalc` to Determine Map Projection Geometric Distortions