地球的形状
尽管地球非常圆,但它是一个扁的椭球体而非完美的球体。这种差异极其微小(仅为 300 分之 1),因此将地球视为球体足以满足绘制小比例尺(世界或大陆)地图的需求。然而,要绘制更大比例尺的精确地图,则必须采用椭球体模型。此类模型至关重要,例如在绘制高分辨率卫星或航空影像时,或处理全球定位系统 (GPS) 坐标时。本节阐述了 Mapping Toolbox™ 软件如何精确建模地球的形状或轮廓。
椭球体形状
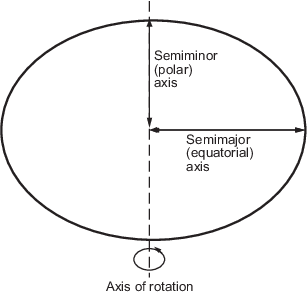
您可以通过多种方式定义椭球体。它们通常由一个半长轴和一个半短轴来定义,但常以半长轴配合扁率倒数(如前所述,地球的扁率倒数为 300 分之一)或偏心率来表示。无论采用何种参数,只要包含轴长,椭球体即被完全约束,其余参数均可推导得出。椭球体的各部分如图所示。
该工具箱包含代表太阳、月亮和行星形状的椭球体模型,以及一套最常用的地球椭球体模型。有关详细信息,请参阅Comparison of Reference Spheroids。
大地水准面形状
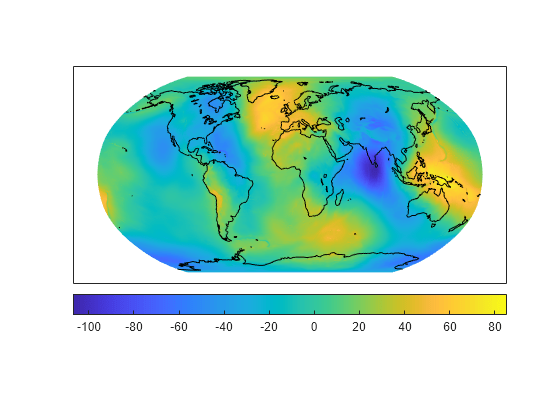
字面意思上,geoid(大地水准面)意为地球形状。大地水准面是对地球形状(减去地形起伏)的一种经验近似,即地球的"凹凸不平"。具体而言,它是一个重力等势面,大致对应于平均海平面。它近似为一个椭球体,但并非完全吻合,因为重力在局部区域的差异形成了微小的山丘与谷地(其高度范围在地球表面从-100 米到+60 米之间)。这种高度差异约为椭球体长半轴与短半轴之间差异的 1%,而椭球体正是用于近似描述地球形状的几何模型。
大地水准面的形状对于某些用途(如计算卫星轨道)至关重要,但并非所有测绘应用都需要考虑它。然而,有时需要了解大地水准面,例如在比较以平均海平面高度表示的海拔与基于 GPS 测量得出的海拔时。大地水准面表示法同样是基准面定义的内在组成部分。
绘制大地水准面
从 EGM96 大地水准面模型获取大地水准面高程及地理坐标参考对象。加载海岸线纬度和经度数据。
[N,R] = egm96geoid;
load coastlines使用罗宾逊投影将大地水准面高程以曲面形式显示。通过将 'CData' 名称-值对设置为大地水准面高程数据,并将 'ZData' 名称-值对设置为全零矩阵,确保海岸线数据显示在表面之上。然后,显示海岸线数据。
axesm robinson Z = zeros(R.RasterSize); geoshow(N,R,'DisplayType','surface','CData',N,'ZData',Z) geoshow(coastlat,coastlon,'color','k')
在地图下方显示一个颜色栏。
colorbar('southoutside')