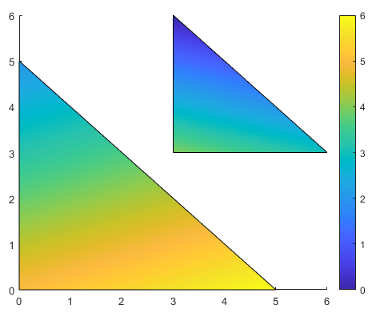补片数据与颜色图的关系
在创建使用 Patch 对象的图形时,可以通过调用 colormap 函数来控制总体颜色方案。您也可以通过以下方式控制颜色图与补片之间的关系:
为面分配特定颜色
为各个面周围的顶点分配特定颜色
您控制这些关系的方式取决于您指定补片的方式:是指定为 x、y、z 坐标,还是指定为面-顶点数据。
颜色图与 x、y、z 坐标数组的关系
如果您使用 x、y、z 坐标数组创建 Patch 对象,Patch 对象的 CData 属性将包含索引数组 C。此数组控制颜色图与补片之间的关系。要为面分配颜色,应将 C 指定为具有以下特征的数组:
C为 n×1 数组,其中 n 为面数。C(i)处的值控制面i的颜色。
下面的示例演示了 C 及其与颜色图和三个面的关系。C(i) 的值控制顶点 (X(i,:), Y(i,:)) 定义的面的颜色。
C 的最小值为 0。它映射到颜色图中的第一行。C 的最大值为 1,它映射到颜色图中的最后一行。C 的中间值线性映射到颜色图的中间行。在本例中,C(2) 映射到距离颜色图起始点约三分之二处的颜色。此代码将创建先前图示中所描述的 Patch 对象。
X = [0 0 5; 0 0 5; 4 4 9]; Y = [0 4 0; 3 7 3; 0 4 0]; C = [0; .6667; 1]; p = patch(X,Y,C); colorbar
要为顶点分配颜色,应将 C 指定为具有以下特征的数组:
C为 m×n 数组,其中 m 为每个面的顶点数,n 为面数。C(i,j)处的值控制面j的顶点i处的颜色。
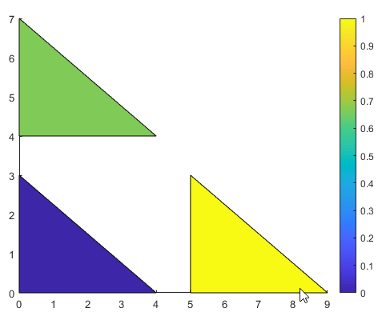
下面的示例演示了 C 及其与颜色图和六个顶点之间的关系。C(i,j) 的值控制 (X(i,j), Y(i,j)) 处的顶点的颜色。
与补片面一样,MATLAB® 可将 C 中的值缩放映射到颜色图中的行数。在本例中,最小值为 C(2,2)=1,它映射到颜色图中的第一行。最大值为 C(3,1)=6,它映射到颜色图中的最后一行。
此代码将创建先前图示中所描述的 Patch 对象。FaceColor 属性设置为 'interp',以使顶点颜色在各个面之间混合。
clf X = [0 3; 0 3; 5 6]; Y = [0 3; 5 6; 0 3]; C = [5 4; 2 0; 6 3]; p = patch(X,Y,C,'FaceColor','interp'); colorbar
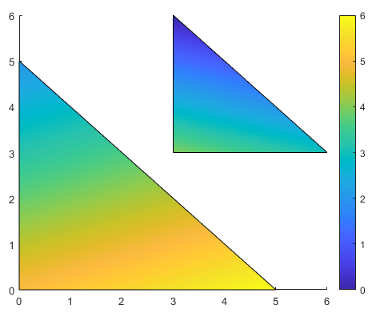
颜色图与面-顶点数据的关系
如果是使用面-顶点数据创建补片,Patch 对象的 FaceVertexCData 属性将包含索引数组 C。此数组控制颜色图与补片之间的关系。
要为面分配颜色,应将 C 指定为具有以下特征的数组:
C为 n×1 数组,其中 n 为面数。C(i)处的值控制面i的颜色。
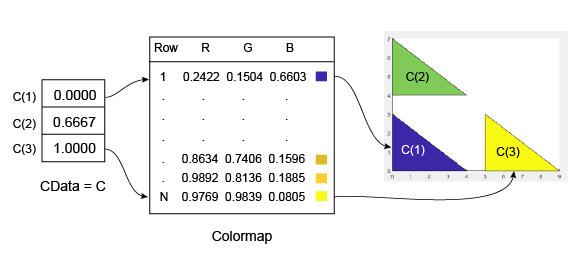
下面的示例演示了 C 及其与颜色图和三个面的关系。
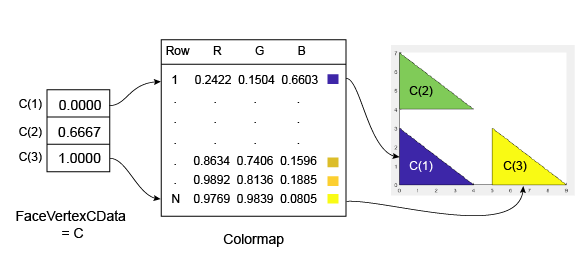
C 的最小值为 0,它映射到颜色图中的第一行。C 的最大值为 1,它映射到颜色图中的最后一个值。C 的中间值线性映射到颜色图的中间行。在本例中,C(2) 映射到距离颜色图底部约三分之二处的颜色。
此代码将创建先前图示中所描述的 Patch 对象。FaceColor 属性设置为 'flat',以显示颜色图的颜色而不显示默认颜色(黑色)。
clf vertices = [0 0; 0 3; 4 0; 0 4; 0 7; 4 4; 5 0; 5 3; 9 0]; faces = [1 2 3; 4 5 6; 7 8 9]; C = [0; 0.6667; 1]; p = patch('Faces',faces,'Vertices',vertices,'FaceVertexCData',C); p.FaceColor = 'flat'; colorbar

要为顶点分配颜色,应将 Patch 对象的 FaceVertexCData 属性指定为具有以下特征的数组 C:
C为 n×1 数组,其中 n 为顶点数。C(i)处的值控制顶点i的颜色。
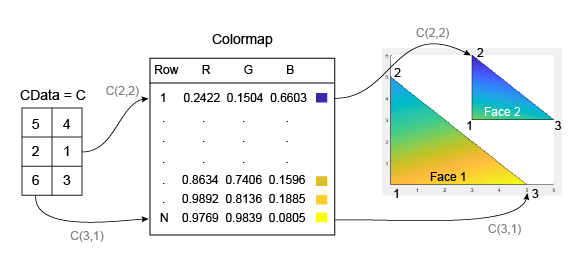
下面的示例演示了 C 及其与颜色图和六个顶点之间的关系。
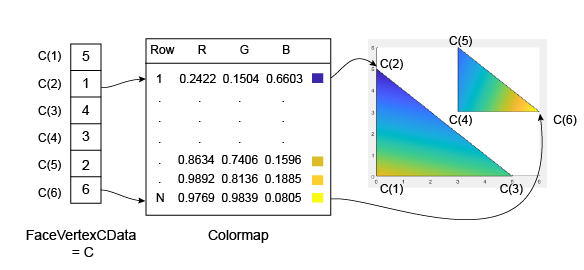
与补片面一样,MATLAB 可将 C 中的值缩放映射到颜色图中的行数。在本例中,最小值为 C(2)=1,它映射到颜色图中的第一行。最大值为 C(6)=6,它映射到颜色图中的最后一行。
此代码将创建先前图示中所描述的 Patch 对象。FaceColor 属性设置为 'interp',以使顶点颜色在各个面之间混合。
clf vertices = [0 0; 0 5; 5 0; 3 3; 3 6; 6 3]; faces = [1 2 3; 4 5 6]; C = [5; 1; 4; 3; 2; 6]; p = patch('Faces',faces,'Vertices',vertices,'FaceVertexCData',C); p.FaceColor = 'interp'; colorbar