绘制复数

绘制复数数组

创建一个包含复数 3 + 4i、-4 - 3i、1 - 2i 和 -1 - 1i 的向量。

z = [3 + 4i; -4 - 3i; 1 - 2i; -1 - 1i]

z = 4×1 complex

   3.0000 + 4.0000i
  -4.0000 - 3.0000i
   1.0000 - 2.0000i
  -1.0000 - 1.0000i

使用 plot 绘制复数向量 z 的虚部对实部的图。使用 real 函数和 imag 函数分别返回复数向量的实部和虚部。

plot(real(z),imag(z),"o")
axis equal
grid on
xlabel("Re(z)")
ylabel("Im(z)")

您还可以使用 plot(z,LineSpec) 而不是 plot(real(z),imag(z),LineSpec) 来绘制复数数组。此函数自动绘制 $$x$$ 轴上的实部和 $$y$$ 轴上的虚部。

在笛卡尔坐标中绘制复单位根

单位的 $$n$$ 次根是满足多项式方程的复数

${\mathit{z}}^{\mathit{n}}=1$,

其中 $$n$$ 是正整数。

单位的 $$n$$ 次根是

$\exp \left(\frac{2\mathit{k}\pi \mathrm{i}}{\mathit{n}}\right)=\cos \frac{2\mathit{k}\pi }{\mathit{n}}+\mathrm{i}\sin \frac{2\mathit{k}\pi }{\mathit{n}}$，$\mathit{k}=0,1,\dots ,\mathit{n}-1$。

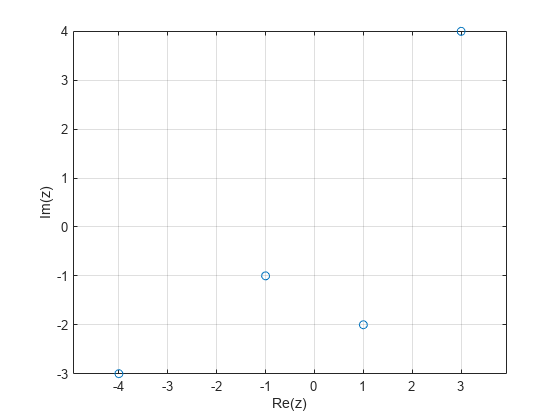
要求出单位的复根，可以使用 roots 求解多项式方程。roots 函数对 ${\mathit{p}}_1{\mathit{x}}^{\mathit{n}}+\cdots +{\mathit{p}}_{\mathit{n}}\mathit{x}+{\mathit{p}}_{\mathit{n}+1}=0$ 格式的多项式方程求解。例如，求 $$z^5=1$$ 或 $$z^5-1=0$$ 的 5 次单位根。

p = [1 0 0 0 0 -1];
z = roots(p)

z = 5×1 complex

  -0.8090 + 0.5878i
  -0.8090 - 0.5878i
   0.3090 + 0.9511i
   0.3090 - 0.9511i
   1.0000 + 0.0000i

在笛卡尔坐标中绘制复单位根。

plot(z,"o")
axis equal
grid on
xlabel("Re(z)")
ylabel("Im(z)")

在极坐标中绘制复数

使用 polarplot 在极坐标中绘制 5 次单位根。使用 angle 函数返回复根的相位角，使用 abs 函数返回复根的绝对值或半径。

polarplot(angle(z),abs(z),"o")

您还可以使用 polarplot(z,LineSpec) 而不是 polarplot(angle(z),abs(z),LineSpec) 来绘制极坐标中的复数数组。此函数自动绘制复数的半径和相位角。

在复平面中绘制参数化曲线

定义以下形式的参数化曲线

其中，参数 $$t$$ 在区间 $$[0,4\pi ]$$ 中。

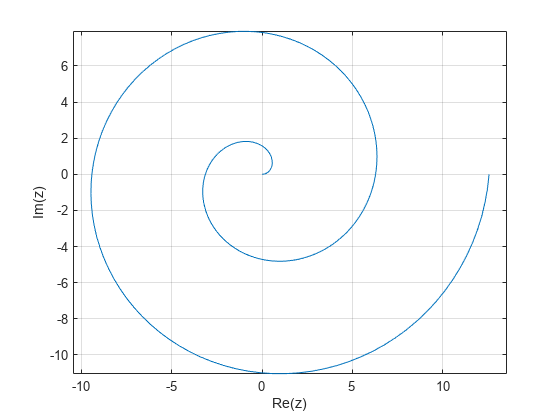
在此区间内创建一个包含 200 个等间距点的向量 t 以参数化 $$t$$。将位于复曲线上的点定义为复数向量 z。

t = linspace(0,4*pi,200);
z = t.*exp(1i*t);

在笛卡尔坐标中绘制复曲线。

plot(z,"-")
axis equal
grid on
xlabel("Re(z)")
ylabel("Im(z)")

在极坐标中绘制复曲线。

polarplot(z,"-")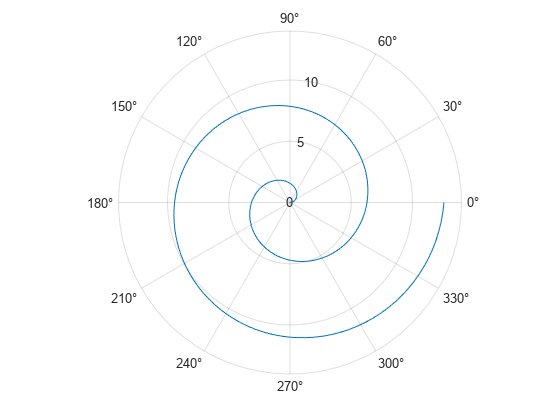

绘制方阵的特征值

一个 $$n$$×$$n$$ 实数方阵有 $$n$$ 个特征值（包括代数重数），这些特征值或者是实数，或者出现在复共轭对组中。

例如，假设有一个 20×20 实矩阵，其随机元素是从标准正态分布中采样的。使用 eig 计算特征值。

rng("default")
z = eig(randn(20));

绘制所有 20 个特征值的虚部对实部的图。请注意，对于不在实轴上的每个特征值 $$z_k=x_k+y_{k}i$$，此特征值还有另一个复共轭对组 $$z_k^{*}=x_k-y_{k}i$$。

plot(z,"o")
axis equal
grid on
xlabel("Re(z)")
ylabel("Im(z)")

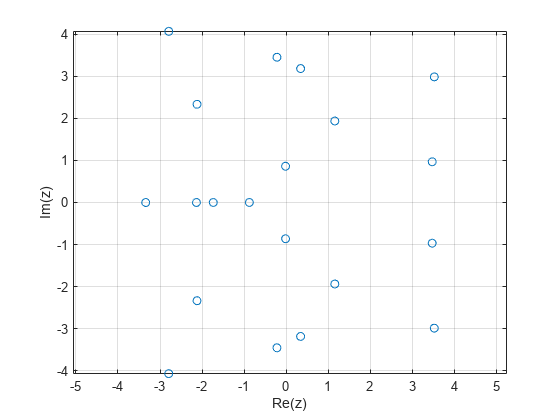
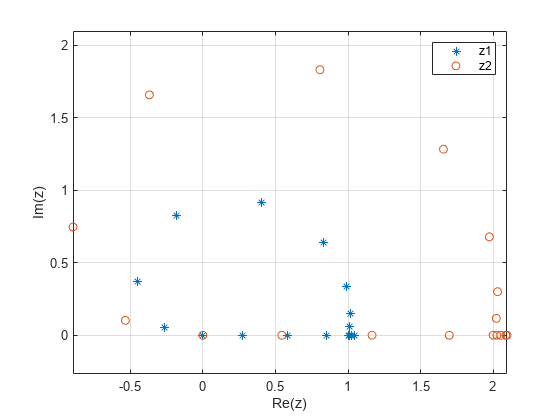
绘制多个复数数据集

绘制两个复数数据集的虚部对实部的图。如果您将多个复数输入参量传递给 plot，例如 plot(z1,z2)，则 plot 函数将忽略输入的虚部，而仅绘制实部。要为多个复数输入绘制多个实部对虚部的图，必须将实部和虚部显式传递给 plot。

例如，创建两个复数向量 z1 和 z2。

x = -2:0.25:2;
z1 = x.^exp(-x.^2);
z2 = 2*x.^exp(-x.^2);

通过使用 real 和 imag 函数求出每个向量的实部和虚部。

re_z1 = real(z1);
im_z1 = imag(z1);
re_z2 = real(z2);
im_z2 = imag(z2);

绘制复数数据。

plot(re_z1,im_z1,"*",re_z2,im_z2,"o")
axis equal
grid on
legend("z1","z2")
xlabel("Re(z)")
ylabel("Im(z)")