修改 alphamap
每个图窗都有一个关联的 alphamap,它是一组 0 到 1 之间的向量值。默认的 alphamap 包含 0 到 1 范围内的 64 个线性变化值。可以使用图窗的 Alphamap 属性或使用 alphamap 函数来查看或修改 alphamap。
默认的 alpha 映射
默认的 alphamap 包含 0 到 1 范围内的 64 个线性变化值,如下图所示。
am = get(gcf,'Alphamap'); plot(am)
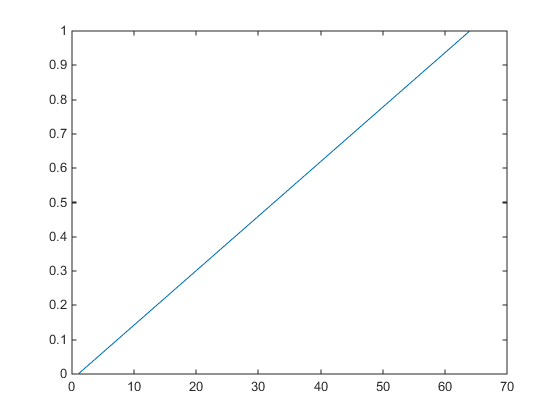
此 alphamap 将最低的 alpha 数据值显示为完全透明,将最高的 alpha 数据值显示为完全不透明。
alphamap 函数可以创建一些有用的预定义 alphamap,还可以修改现有 alphamap。例如,
figure;
alphamap('vup')
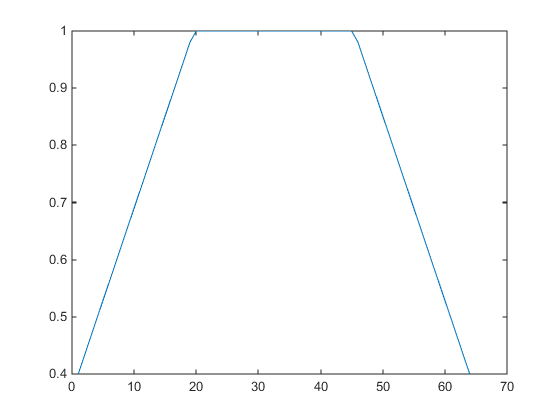
将图窗的 Alphamap 属性设置为值先增后减的 alphamap:
am = get(gcf,'Alphamap');
plot(am)

您可以使用 increase 或 decrease 选项改变这些值。例如,
alphamap('increase',.4)
将图窗当前 alphamap 中的所有值加上 0.4。重新绘制 'vup' alphamap 可以看出变化。这些值限制在 [0 1] 的范围内。
am = get(gcf,'Alphamap'); plot(am)
示例 - 修改 alphamap
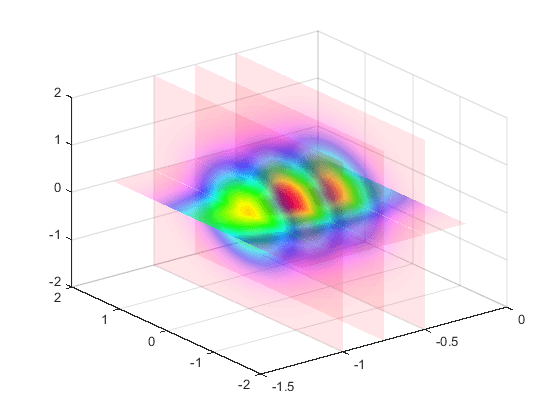
此示例使用切片平面来查看三维体数据。切片平面使用颜色数据作为 alpha 数据,并使用递减的 alphamap(值范围从 1 到 0):
通过计算一个包含三个变量的函数来创建三维体数据。
[x,y,z] = meshgrid(-1.25:.1:-.25,-2:.2:2,-2:.1:2); v = x.*exp(-x.^2-y.^2-z.^2);
创建切片平面,将 alpha 数据设置为等于颜色数据,并指定
FaceColor和FaceAlpha插值。h = slice(x,y,z,v,[-1 -.75 -.5],[],[0]); set(h,'EdgeColor','none',... 'FaceColor','interp',... 'FaceAlpha','interp') alpha('color')使用不透明度线性递减的 alphamap 并通过将 alphamap 中的每个值增加 0.1 来实现所需的透明度。指定
hsv颜色图。alphamap('rampdown') alphamap('increase',.1) colormap hsv
此 alphamap 用最小的透明度显示函数的最小值(接近零),用最大的透明度显示函数的最大值。这使您能够透视切片平面,同时保留了零附近的数据。