Main Content

有限差分拉普拉斯算子

打开实时脚本

此示例说明如何在 L 形域中计算和表示有限差分拉普拉斯算子。

域

numgrid 函数为 L 形域内的点编号。spy 函数可用于可视化矩阵中非零元素的模式。使用这两个函数生成并显示 L 形域。

n = 32;
R = 'L';
G = numgrid(R,n);
spy(G)
title('A Finite Difference Grid')

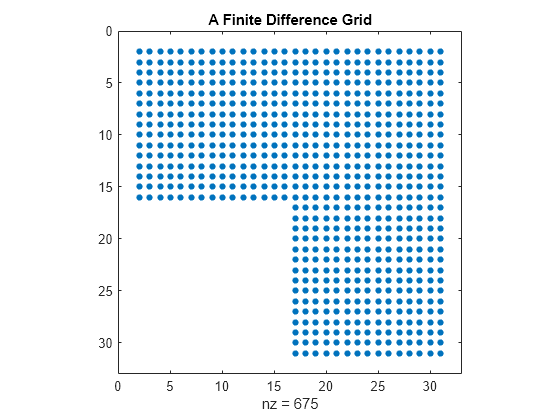
Figure contains an axes object. The axes object with title A Finite Difference Grid, xlabel nz = 675 contains a line object which displays its values using only markers.

取一个较小版本的矩阵作为样例。

g = numgrid(R,10)
g = 10×10

     0     0     0     0     0     0     0     0     0     0
     0     1     5     9    13    17    25    33    41     0
     0     2     6    10    14    18    26    34    42     0
     0     3     7    11    15    19    27    35    43     0
     0     4     8    12    16    20    28    36    44     0
     0     0     0     0     0    21    29    37    45     0
     0     0     0     0     0    22    30    38    46     0
     0     0     0     0     0    23    31    39    47     0
     0     0     0     0     0    24    32    40    48     0
     0     0     0     0     0     0     0     0     0     0

离散拉普拉斯算子

使用 delsq 生成离散拉普拉斯算子。同样使用 spy 函数显示矩阵元素的图形效果。

D = delsq(G);
spy(D)
title('The 5-Point Laplacian')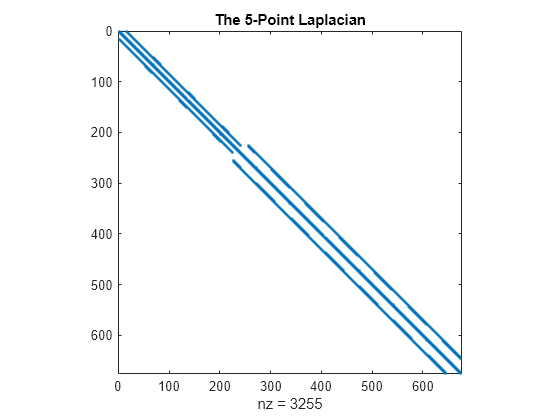

Figure contains an axes object. The axes object with title The 5-Point Laplacian, xlabel nz = 3255 contains a line object which displays its values using only markers.

确定内部点的数量。

N = sum(G(:)>0)
N = 
675

狄利克雷边界值问题

求解稀疏线性系统的狄利克雷边界值问题。问题设置：

delsq(u) = 1 在内部，u = 0 在边界上。

rhs = ones(N,1);
if (R == 'N') % For nested dissection, turn off minimum degree ordering.
   spparms('autommd',0)
   u = D\rhs;
   spparms('autommd',1)
else
   u = D\rhs; % This is used for R=='L' as in this example
end

将解映射到 L 形网格并绘制等高线图。

U = G;
U(G>0) = full(u(G(G>0)));
clabel(contour(U));
prism
axis square ij

Figure contains an axes object. The axes object contains 15 objects of type contour, line, text.

现在，以网格图形式呈现该解。

mesh(U)
axis([0 n 0 n 0 max(max(U))])
axis square ij

Figure contains an axes object. The axes object contains an object of type surface.

另请参阅