基本运算的兼容数组大小

MATLAB^® 中的大多数二元（两个输入）运算符和函数都支持具有兼容大小的数值数组。对于每个维度，如果两个输入的维度大小相同或其中一个为 1，则这些输入将具有兼容的大小。以最简单的情况为例，如果两个数组大小完全相同或其中一个为标量，则这两个数组大小是兼容的。执行按元素运算或函数时，MATLAB 会将大小兼容的数组隐式扩展为相同的大小。

大小兼容的输入

二维输入

以下是一些具有兼容大小的标量、向量和矩阵的组合：

两个大小完全相同的输入。
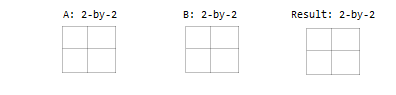
一个输入是标量。
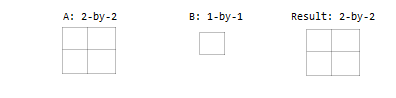
一个输入是矩阵，另一个输入是具有相同行数的列向量。
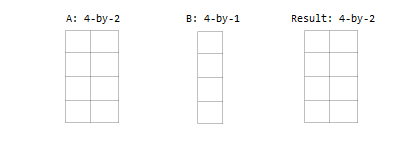
一个输入是列向量，另一个输入是行向量。

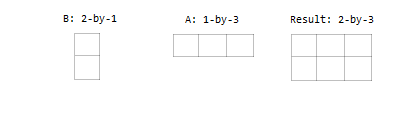
多维数组

MATLAB 中的每个数组都具有大小为 1 的尾部维度。对于多维数组，这意味着 3×4 矩阵与大小为 3×4×1×1×1 的矩阵相同。具有兼容大小的多维数组的示例如下：

一个输入是矩阵，另一个输入是具有相同行数和列数的三维数组。
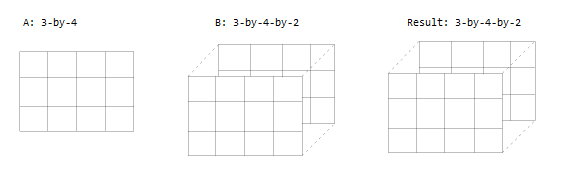
一个输入是矩阵，另一个输入是三维数组。这些维度要么都相同，要么其中一个为 1。

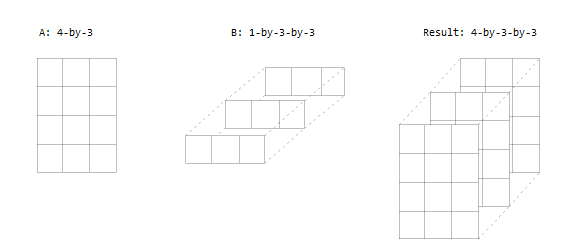
空数组

对于空数组或维度大小为零的数组，规则是相同的。不等于 1 的维度大小确定输出的大小。这意味着，大小为零的维度必须与另一个数组中大小为 1 或 0 的维度进行配对，并且输出的维度大小为 0。

     A: 1-by-0     
     B: 3-by-1
Result: 3-by-0

大小不兼容的输入

不兼容的输入的大小无法隐式扩展为相同的大小。例如：

其中一个维度大小不相等，并且维度大小均不为 1。
```
A: 3-by-2
B: 4-by-2
```
两个长度不相同的非标量行向量。
```
A: 1-by-3
B: 1-by-4
```

示例

从矩阵减去向量

要简化向量-矩阵运算，请对维函数（例如 sum、mean、min 以及其他）使用隐式扩展。

例如，计算矩阵中每列的均值，然后从每个元素中减去均值。

A = magic(3)

A =

     8     1     6
     3     5     7
     4     9     2

C = mean(A)

C =

     5     5     5

A - C

ans =

     3    -4     1
    -2     0     2
    -1     4    -3

行向量和列向量相加

行向量和列向量的大小兼容，当您对它们执行运算时，结果为一个矩阵。

例如，将行向量和列向量相加。结果与 bsxfun(@plus,a,b) 相同。

a = [1 2 3 4]

ans =

     1     2     3     4

b = [5; 6; 7]

a + b

ans =

     6     7     8     9
     7     8     9    10
     8     9    10    11

另请参阅

bsxfun