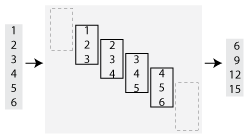
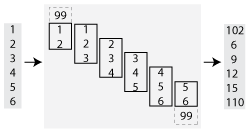
matlab.tall.blockMovingWindow

将移动窗函数和块约简应用于填充的数据块

全页折叠

语法

tA = matlab.tall.blockMovingWindow(windowfcn,blockfcn,window,tX)
[tA,tB,...] = matlab.tall.blockMovingWindow(windowfcn,blockfcn,window,tX,tY,...)
[___] = matlab.tall.blockMovingWindow(___,Name,Value)

说明

tA = matlab.tall.blockMovingWindow(windowfcn,blockfcn,window,tX) 将 blockfcn 应用于完整的数据窗，将 windowfcn 应用于边附近的不完整数据窗。window 指定滑动窗的大小。结果包含将 blockfcn 和 windowfcn 应用于这些数据窗口的垂直串联。

示例

[tA,tB,...] = matlab.tall.blockMovingWindow(windowfcn,blockfcn,window,tX,tY,...)（其中 windowfcn 和 blockfcn 是返回多个输出的函数句柄）返回数组 tA, tB, ...，其中每个数组对应于 windowfcn 和 blockfcn 的一个输出参量。对 windowfcn 和 blockfcn 的输入是来自 tX, tY, ... 参量的数据片段。此语法具有以下要求：

  • windowfcn 和 blockfcn 返回的输出数目必须与从 matlab.tall.blockMovingWindow 请求的输出数目相同。

  • windowfcn 和 blockfcn 的每个输出必须与第一个数据输入 tX 的输出类型相同。

  • 所有输出 tA,tB,... 必须具有相同的高度。

示例

[___] = matlab.tall.blockMovingWindow(___,Name,Value) 支持任何上述语法，且可使用一个或多个名称-值对组参量指定其他选项。例如，要调整窗口之间的步长，可以指定 'Stride' 和一个标量。或者，要在没有足够元素来完成窗口的情况下更改端点处理，您可以指定 'EndPoints' 和一个有效选项（'shrink'、'discard' 或数值填充值）。

示例

示例

全部折叠

打开实时脚本

使用 matlab.tall.blockMovingWindow 计算航班到港和离港延误的移动均值。

为 airlinesmall.csv 数据集创建一个数据存储，并将其转换为 tall 数组。该数据包含有关美国航班的到港和离港时间的信息。提取 ArrDelay 和 DepDelay 变量（它们是航班延误数据的向量），以创建两者延误数据分别位于单独列中的 tall 数组。

varnames = {'ArrDelay', 'DepDelay'};
ds = tabularTextDatastore('airlinesmall.csv', 'TreatAsMissing', 'NA', ...
    'SelectedVariableNames', varnames);
tt = tall(ds);
tX = [tt.ArrDelay tt.DepDelay]
tX =

  M×2 tall double matrix

     8    12
     8     1
    21    20
    13    12
     4    -1
    59    63
     3    -2
    11    -1
    :     :
    :     :

使用 matlab.tall.blockMovingWindow 计算窗口大小为 10 的第一个维度中数据的移动均值。由于 windowfcn 仅应用于单个数据窗口，您可以使用 mean 函数将数据窗口约简为具有一行的矩阵。blockfcn 应用于整个数据块，因此使用 movmean 函数计算数据块中每个完整数据窗口的均值。

windowfcn = @(info,x) mean(x,1,'omitnan');
blockfcn = @(info,x) movmean(x,info.Window,1,'omitnan','EndPoints','discard');
A = matlab.tall.blockMovingWindow(windowfcn, blockfcn, 10, tX)
A =

  M×N×... tall double array

    ?    ?    ?    ...
    ?    ?    ?    ...
    ?    ?    ?    ...
    :    :    :
    :    :    :

Preview deferred. Learn more.

将部分结果收集到内存中。

gather(A(1:10,:))
Evaluating tall expression using the Local MATLAB Session:
- Pass 1 of 2: Completed in 0.55 sec
- Pass 2 of 2: Completed in 1.6 sec
Evaluation completed in 2.5 sec

ans = 10×2

   10.8000    8.8000
   18.8333   17.8333
   16.5714   15.0000
   15.8750   13.0000
   14.4444   11.8889
   13.2000   10.8000
   14.0000   11.1000
   13.5000   11.9000
   15.3000   11.4000
   19.7000   13.4000
打开实时脚本

计算表变量的移动统计量信息。

将 outages.csv 数据集作为 tall 表加载。数据包含停电信息。

T = tall(readtable('outages.csv'))
T =

  1,468×6 tall table

       Region           OutageTime        Loss     Customers     RestorationTime            Cause       
    _____________    ________________    ______    __________    ________________    ___________________

    {'SouthWest'}    2002-02-01 12:18    458.98    1.8202e+06    2002-02-07 16:50    {'winter storm'   }
    {'SouthEast'}    2003-01-23 00:49    530.14    2.1204e+05                 NaT    {'winter storm'   }
    {'SouthEast'}    2003-02-07 21:15     289.4    1.4294e+05    2003-02-17 08:14    {'winter storm'   }
    {'West'     }    2004-04-06 05:44    434.81    3.4037e+05    2004-04-06 06:10    {'equipment fault'}
    {'MidWest'  }    2002-03-16 06:18    186.44    2.1275e+05    2002-03-18 23:23    {'severe storm'   }
    {'West'     }    2003-06-18 02:49         0             0    2003-06-18 10:54    {'attack'         }
    {'West'     }    2004-06-20 14:39    231.29           NaN    2004-06-20 19:16    {'equipment fault'}
    {'West'     }    2002-06-06 19:28    311.86           NaN    2002-06-07 00:51    {'equipment fault'}
          :                 :              :           :                :                     :
          :                 :              :           :                :                     :

使用 matlab.tall.blockMovingWindow 将移动窗函数应用于 tall 表的数据块。指定下列选项：

  • 将 blkstats 指定为对完整数据块进行操作的块函数（作为局部函数包含在示例末尾）。

  • 窗口大小为 50，步幅为 5。

  • 将 EndPoints 指定为 'discard' 以忽略不完整的数据窗口。使用此值，windowfcn 输入可以指定为空的 []，因为只对完整的数据窗口进行操作。

  • 输入表有六个变量，但两个输出是双精度向量。将双精度标量指定为 OutputsLike 的值，以便该函数允许数据类型和大小的这种更改。

[A, B] = matlab.tall.blockMovingWindow([], @blkstats, 50, T, 'Stride', 5, ...
    'EndPoints', 'discard', 'OutputsLike', {1, 1});

预览结果中的几行。

[A,B] = gather(head(A),head(B))
Evaluating tall expression using the Local MATLAB Session:
- Pass 1 of 2: Completed in 0.33 sec
- Pass 2 of 2: Completed in 0.4 sec
Evaluation completed in 1.2 sec

A = 8×1

  254.0861
  254.0861
  340.3499
  452.0191
  464.8524
  471.9737
  464.8524
  464.8524


B = 8×1
105 ×

    1.3447
    1.0779
    1.4227
    1.4509
    1.2888
    1.2888
    1.2308
    1.3722

blkstats 函数使用指定的窗口大小计算第一个维度中 Loss 和 Customers 表变量的移动中位数值。该函数应用 Stride 值来约简输出的大小，然后以两个向量形式返回结果。

function [out1, out2] = blkstats(info, t)
    a = movmedian([t.Loss t.Customers], info.Window, 1, 'omitnan', 'EndPoints', 'discard');
    a = a(1:info.Stride:end, :);
    out1 = a(:,1);
    out2 = a(:,2);
end

输入参数

全部折叠

应用于不完整数据窗口的函数，指定为函数句柄、匿名函数或 []。当在 tall 维度的数据上进行移动窗口计算时，对于每个不完整窗口，都要调用一次 windowfcn。matlab.tall.blockMovingWindow 仅当 'EndPoints' 的默认值为 'shrink' 时才会应用 windowfcn。如果您为 'EndPoints' 指定不同值，则将 windowfcn 设置为 []。

windowfcn 的每个输出必须与第一个数据输入 tX 的类型相同。您可以使用 'OutputsLike' 选项返回不同数据类型的输出。

windowfcn 的一般函数签名是

[a, b, c, ...] = windowfcn(info, x, y, ...)
info 输入是由 matlab.tall.blockMovingWindow 提供的结构体，包括以下字段：

  • Stride - 指定的窗口之间的步长（默认值：1）。使用 'Stride' 名称-值对组设置此值。

  • Window - 指定的窗口大小。使用 window 输入参量设置此值。

windowfcn 必须满足以下要求：

  1. 输入参量 - 输入 [x, y, z, ...] 是内存数据块。通过分别从各个 tall 数组输入 [tX, tY, tZ, ...] 中提取数据来生成这些数据块。输入 [x, y, z, ...] 满足以下属性：

    • 所有输入 [x, y, z, ...] 在第一个维度中具有相同的大小。

    • [x, y, z, ...] 中的数据块来自 tall 维度中的相同索引（假设 tall 数组的 tall 维度是非单一维度）。例如，如果 tX 和 tY 的 tall 维度为非单一维度，则第一组数据块可能是 x = tX(1:20000,:) 和 y = tY(1:20000,:)。

    • 当任一 [tX, tY, tZ, ...] 的第一个维度的大小为 1 时，对应的块 [x, y, z, ...] 包含该 tall 数组中的所有数据。

    • 应用 windowfcn 对输入数据进行约简后，结果必须是标量或高度为 1 的数组切片。

      当输入是矩阵、N 维数组、表或时间表时，应用 windowfcn 必须对输入数据的每列或每个变量都进行约简。

  2. 输出参量 - 输出 [a, b, c, ...] 是可放入内存的数据块，将被发送到对应的输出 [tA, tB, tC, ...]。输出 [a, b, c, ...] 满足以下属性：

    • 所有输出 [a, b, c, ...] 的第一个维度必须具有相同的维度。

    • 所有输出 [a, b, c, ...] 与先前对 windowfcn 的调用的对应结果垂直串联。

    • 所有输出 [a, b, c, ...] 都将发送到各自目标输出数组中第一个维度中的相同索引。

  3. 函数规则 - windowfcn 必须满足以下函数规则：

    • F([inputs1; inputs2]) == [F(inputs1); F(inputs2)]:将函数应用于输入的串联应该等效于将函数分别应用于各输入，然后对结果进行串联。

示例: A = matlab.tall.blockMovingWindow(@windowfcn, @blockfcn, 10, tX)

示例: A = matlab.tall.blockMovingWindow([], @blockfcn, 10, tX, 'EndPoints', 'discard')

数据类型: function_handle

应用于数据块的函数，指定为函数句柄或匿名函数。blockfcn 应用于包含完整数据窗口的数据块。因此，blockfcn 必须对整个数据块进行向量化运算，并返回具有适合指定窗口大小和步幅的输出。

blockfcn 的每个输出必须与第一个数据输入 tX 的类型相同。您可以使用 'OutputsLike' 选项返回不同数据类型的输出。

matlab.tall.blockMovingWindow 将 blockfcn 只有在数据块仅包含完整窗口时应用于数据块：

  • 当 'EndPoints' 设置为 'shrink' 时应用于中间块（默认行为）。在这种情况下，windowfcn 对末端不完整的数据窗口进行操作。

  • 当 'EndPoints' 设置为 'discard' 或填充值时，应用于所有块。

blockfcn 的一般函数签名是

[a, b, c, ...] = blockfcn(info, bX, bY, bZ, ...)
info 输入是由 matlab.tall.blockMovingWindow 提供的结构体，包括以下字段：

  • Stride - 指定的窗口之间的步长（默认值：1）。使用 'Stride' 名称-值对组设置此值。

  • Window - 指定的窗口大小。使用 window 输入参量设置此值。

matlab.tall.blockMovingWindow 向 blockfcn 提供的数据块 bX, bY, bZ, ... 具有以下属性：

  • 这些数据块只包含完整大小的窗口。blockfcn 不必为不完整的数据窗口定义行为。

  • 第一个数据窗口从数据块的第一个元素开始。最后一个窗口的最后一个元素是数据块的最后一个元素。

blockfcn 必须满足以下要求：

  1. 输入参量 - 输入 [bX, bY, bZ, ...] 是内存数据块。通过分别从各个 tall 数组输入 [tX, tY, tZ, ...] 中提取数据来生成这些数据块。输入 [bX, bY, bZ, ...] 满足以下属性：

    • 进行任何允许的扩展后，所有输入 [bX, bY, bZ, ...] 在第一个维度中具有相同的维度。

    • [bX, bY, bZ, ...] 中的数据块来自 tall 维度中的相同索引（假设 tall 数组的 tall 维度是非单一维度）。例如，如果 tX 和 tY 的 tall 维度为非单一维度，则第一组数据块可能是 bX = tX(1:20000,:) 和 bY = tY(1:20000,:)。

    • 如果任一数据输入 [tX, tY, tZ, ...] 的第一个维度的大小为 1，则对应的块 [bX, bY, bZ, ...] 包含该 tall 数组中的所有数据。

    • 应用 blockfcn 对输入数据进行约简后的结果的高度必须等于数据块中的窗口数。您可以使用 info.Window 和 info.Stride 来确定一个数据块中的窗口数量。

      如果输入是矩阵、N 维数组、表或时间表，则应用 blockfcn 必须对输入数据的每列或每个变量都进行约简。

  2. 输出参量 - 输出 [a, b, c, ...] 是可放入内存的数据块，将被发送到对应的输出 [tA, tB, tC, ...]。输出 [a, b, c, ...] 满足以下属性：

    • 所有输出 [a, b, c, ...] 的第一个维度必须具有相同的维度。

    • 所有输出 [a, b, c, ...] 与先前对 blockfcn 的调用的对应结果垂直串联。

    • 所有输出 [a, b, c, ...] 都将发送到各自目标输出数组中第一个维度中的相同索引。

  3. 函数规则 - blockfcn 必须满足以下函数规则：

    • F([inputs1; inputs2]) == [F(inputs1); F(inputs2)]:将函数应用于输入的串联应该等效于将函数分别应用于各输入，然后对结果进行串联。

示例: A = matlab.tall.blockMovingWindow(@windowfcn, @blockfcn, 10, tX)

示例: A = matlab.tall.blockMovingWindow([], @blockfcn, 10, tX, 'EndPoints', 'discard')

数据类型: function_handle

窗口大小，指定为正整数标量或二元素行向量 [NB NF]。

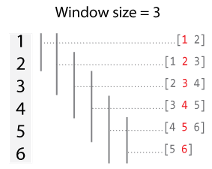
  • 如果 window 是标量，则：

    • 当窗口大小为奇数时，每个窗口都以数据中对应的元素为中心。

      Illustration of a window size of three for a vector with six elements. There are six windows and the first and last windows have two elements such that each window is centered on the corresponding element in the data.

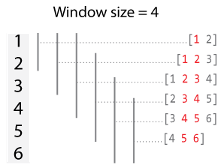
    • 当窗口大小为偶数时，每个窗口都以当前元素及其前一个元素为中心。

      Illustration of a window size of four for a vector with six elements. The first window has two elements, the second has three elements, the next three windows have four elements, and the last window has three elements. Each window is centered about the current and previous elements.

  • 如果 window 是向量 [NB NF]，则窗口包括输入的当前元素及其前面 NB 个元素和后面 NF 个元素。

    Illustration of a window size of [2 2] for a vector with six elements. The first window has three elements, the second has four elements, the next two windows have five elements, the second-to-last window has four elements, and the last window has three elements. Each window includes two previous values (when possible), the current value, and the next two values (when possible).

默认情况下，在端点处如果没有足够元素充满整个窗口大小时，窗口会自动在端点处截断。当窗口以这种方式截断时，函数仅应用于窗口内所含的元素。您可以使用 EndPoints 名称-值对组来更改此行为。

数据类型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

输入数组，指定为标量、向量、矩阵、多维数组、表或时间表的单独参量。输入数组可以是 tall 数组或内存数组。输入数组用作变换函数 fcn 的输入。每个输入数组 tX,tY,... 必须具有相同的高度。

名称-值参数

全部折叠

以 Name1=Value1,...,NameN=ValueN 的形式指定可选参量对组，其中 Name 是参量名称，Value 是对应的值。名称-值参量必须出现在其他参量之后，但对各个参量对组的顺序没有要求。

在 R2021a 之前，使用逗号分隔每个名称和值，并用引号将 Name 引起来。

示例: tA = matlab.tall.blockMovingWindow(@windowfcn, blockfcn, window, tX, 'Stride', 2)

窗口之间的步长，指定为包含 'Stride' 和正整数标量的逗号分隔对组。在 fcn 对数据窗口进行操作后，在对下一个窗口进行操作之前，计算将按照 'Stride' 值步进。将 'Stride' 的值从默认值 1 增加等于通过每隔一个元素或每隔两个元素等进行选取来减小输出的大小。

默认情况下，'Stride' 的值是 1，因此每个窗口都以输入中的每个元素为中心。例如，此处有一个移动和计算，窗口大小为 3，对向量 [1 2 3 4 5 6]' 进行操作：

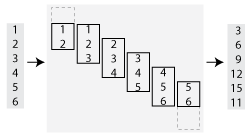
Illustration of a moving sum on a vector with six elements utilizing a stride value of 1. A total of six windows are used in the calculation, so the output has six elements.

如果 'Stride' 的值是 2，则计算会发生变化，每个窗口以输入中的每第二个元素为中心 (1, 3, 5)。移动和现在返回三个部分和，而不是六个：

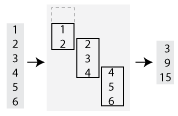
Illustration of a moving sum on a vector with six elements utilizing a stride value of 2. A total of three windows are used in the calculation, so the output has three elements.

数据类型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

用于处理前导和尾部窗的方法，指定为以逗号分隔的对组，包含 'EndPoints' 和下表中的值之一。

在加窗计算的开始和结束时，正在操作的元素的窗口是不完整的。'EndPoints' 选项指定如何处理这些不完整的窗口。

'EndPoints' 值描述示例：移动和

'shrink'

在窗接近输入端点时缩小窗口的大小，从而只包括现有元素。

Illustration of a moving sum on a vector with six elements. Six windows are used in the moving sum, with the windows at the endpoints including two elements and interior windows including three elements.

'discard'

当窗口不与现有元素完全重叠时，不输出任何结果。

Illustration of a moving sum on a vector with six elements. Four windows are used in the moving sum, with all windows including three elements.

数值或逻辑填充值

将不存在的元素替换为指定的数值或逻辑值。

  • 填充值的类型必须与 tX 相同。

  • 第一个维度中填充值的大小必须等于 1，其他维度中的大小必须匹配 tX。

Illustration of a moving sum on a vector with six elements. Six windows are used in the moving sum, with the windows at the endpoints including two elements plus a fill value. The interior windows have three elements.

数据类型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | char | string

输出数组的原型，以逗号分隔的对组形式指定，由 'OutputsLike' 和包含原型数组的元胞数组组成。当您指定 'OutputsLike' 时，matlab.tall.blockMovingWindow 返回的输出数组 tA,tB,... 与指定的原型数组 {PA,PB,...} 具有相同的数据类型和属性。每当输出数组的数据类型不同于输入数组的数据类型时，您必须指定 'OutputsLike'。如果指定 'OutputsLike'，则必须为每个输出指定一个原型数组。

示例: tA = matlab.tall.blockMovingWindow(..., tX, 'OutputsLike', {int8(1)});（其中 tX 是双精度 tall 数组）以 int8（而不是 double）形式返回 tA。

数据类型: cell

输出参量

全部折叠

输出数组，以标量、向量、矩阵或多维数组形式返回。如果 matlab.tall.blockMovingWindow 的任一输入为 tall，则所有输出参量也为 tall。否则，所有输出参量均为内存数组。

  • 输出数组的大小和数据类型取决于指定的窗口函数 windowfcn 和 blockfcn。

  • 输出数组 tA,tB,... 都具有相同的高度，这取决于 'Stride' 和 'EndPoints' 的值。默认情况下，输出数组与输入数组大小相同。

  • 通常，输出 tA,tB,... 必须与第一个数据输入 tX 具有相同的数据类型。但是，您可以指定 'OutputsLike' 以返回不同数据类型。如果输入数组 tX, tY, ... 为空，或 'EndPoints' 为 'discard' 且没有足够的元素来填充完整大小的窗口，matlab.tall.blockMovingWindow 将返回空输出。空输出的大小基于输入数组 tX 的大小，或基于提供给 'OutputsLike' 的原型数组的大小（如果指定）。

提示

  • matlab.tall.movingWindow 用于简单的滑动窗计算。matlab.tall.blockMovingWindow 是一个高级 API，可更灵活地对 tall 数组执行滑动窗计算。因此，它使用起来更加复杂，原因在于函数必须精确地处理包含许多完整窗口的数据块。但是，通过适当的向量化计算，您可以减少必要的函数调用数量并提高性能。

版本历史记录

在 R2019a 中推出

另请参阅

|

主题