Main Content

unmesh

将边矩阵转换为坐标和拉普拉斯矩阵

语法

[L,XY] = unmesh(E)

说明

[L,XY] = unmesh(E) 返回 M×4 边矩阵 E 的拉普拉斯矩阵 L 和网格顶点坐标矩阵 XY。边矩阵的每一行必须包含边端点 [x1 y1 x2 y2] 的坐标。

输入参数

EM×4 边矩阵 E。

输出参量

L图形的拉普拉斯矩阵表示。
XY网格顶点坐标矩阵。

示例

以一个简单的正方形的顶点 (1,1)、(1,–1)、(–1,–1) 和 (–1,1) 为例，连接它的顶点的是正方形的四个垂直边外加 (–1, –1) 与 (1,1) 之间的一个对角线。

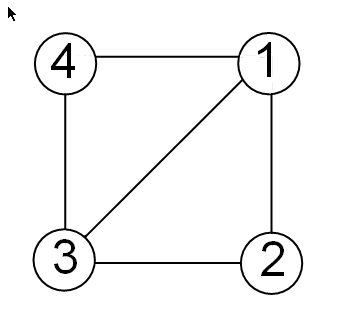
Undirected graph with four nodes

该图形的边矩阵 E 为：

E = [1  1  1 -1;  % edge from 1 to 2
     1 -1 -1 -1;  % edge from 2 to 3 
    -1 -1 -1  1;  % edge from 3 to 4
    -1 -1  1  1;  % edge from 3 to 1
    -1  1  1  1]  % edge from 4 to 1
使用 unmesh 基于边列表创建一个拉普拉斯矩阵和网格坐标矩阵。
[L,XY] = unmesh(E);
拉普拉斯矩阵定义为

Lij={deg(vi)     if i=j−1             if i≠j and vi is adjacent to vj0               otherwise

unmesh 以稀疏矩阵形式返回拉普拉斯矩阵 L。

L
L =

   (1,1)        3
   (2,1)       -1
   (3,1)       -1
   (4,1)       -1
   (1,2)       -1
   (2,2)        2
   (4,2)       -1
   (1,3)       -1
   (3,3)        2
   (4,3)       -1
   (1,4)       -1
   (2,4)       -1
   (3,4)       -1
   (4,4)        3
要采用常规矩阵表示法查看 L，请使用 full 命令。
full(L)
ans =

     3    -1    -1    -1
    -1     2     0    -1
    -1     0     2    -1
    -1    -1    -1     3
网格坐标矩阵 XY 返回正方形各个角的坐标。
XY
XY =

    -1    -1
    -1     1
     1    -1
     1     1

另请参阅

|