Inverse Clarke Transform

实现 αβ 到 abc 的变换

自 R2020a 起

库:
Motor Control Blockset / Controls / Math Transforms
Motor Control Blockset HDL Support / Controls / Math Transforms

描述

Inverse Clarke Transform 模块计算静止 αβ 参考系中平衡的两相正交分量的克拉克逆变换，并输出静止 abc 参考系中平衡的三相分量。该模块也可以计算分量 α、β 和 0 的克拉克逆变换，以输出三相分量 a、b 和 c。对于平衡系统，零分量等于零。使用 Number of inputs 参数以使用两个或三个输入。

该模块接受 α-β 轴分量作为输入，并输出对应的三相信号，其中相位 a 轴与 α 轴对齐。

αβ 参考系中的 α 和 β 输入分量。
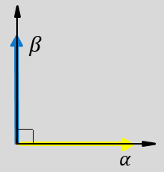
abc 参考系和 αβ 参考系中等效的 a、b 和 c 输出分量的方向。
等效平衡的 αβ 和 abc 系统的单个分量的时间响应。

方程

以下方程描述了克拉克逆变换计算：

$[\begin{matrix} f_{a} \\ f_{b} \\ f_{c} \end{matrix}] = [\begin{matrix} 1 & 0 & 1 \\ - \frac{1}{2} & \frac{\sqrt{3}}{2} & 1 \\ - \frac{1}{2} & - \frac{\sqrt{3}}{2} & 1 \end{matrix}] [\begin{matrix} f_{α} \\ f_{β} \\ f_{0} \end{matrix}]$

对于电机等平衡系统，零序分量计算始终为零：

$i_{a} + i_{b} + i_{c} = 0$

因此，在三相电机驱动中可以只使用两个电流传感器，您可以将其中的第三相计算为，

$i_{c} = - (i_{a} + i_{b})$

通过使用以下方程，该模块将克拉克逆变换实现为，

$[\begin{matrix} \begin{matrix} f_{a} \\ f_{b} \end{matrix} \\ f_{c} \end{matrix}] = [\begin{matrix} \begin{matrix} 1 & 0 \\ - \frac{1}{2} & \frac{\sqrt{3}}{2} \\ - \frac{1}{2} & - \frac{\sqrt{3}}{2} \end{matrix} \end{matrix}] [\begin{matrix} f_{α} \\ f_{β} \end{matrix}]$

其中：

$f_{α}$ 和 $f_{β}$ 是静止 αβ 参考系中的平衡两相正交分量。
$f_{0}$ 是静止 αβ 参考系中的零分量。
$f_{a}$ 、 $f_{b}$ 和 $f_{c}$ 是 abc 参考系中的平衡三相分量。

端口

输入

全部展开

α — 轴分量
标量

静止 αβ 参考系中的 alpha 轴分量 α。

依存关系

要启用此端口，请将 Number of inputs 参数设置为 Two inputs。

数据类型: single | double | fixed point

β — 轴分量
标量

静止 αβ 参考系中的 beta 轴分量 β。

依存关系

要启用此端口，请将 Number of inputs 参数设置为 Two inputs。

数据类型: single | double | fixed point

αβ0 — 轴分量
标量

静止 αβ 参考系中多路复用 alpha 轴分量 α 和 beta 轴分量 β 以及 0 分量。

依存关系

要启用此端口，请将 Number of inputs 参数设置为 Three inputs。

数据类型: single | double | fixed point

输出

全部展开

a — 相分量
标量

abc 参考系中三相系统的分量。

依存关系

要启用此端口，请将 Number of inputs 参数设置为 Two inputs。

数据类型: single | double | fixed point

b — 相分量
标量

abc 参考系中三相系统的分量。

依存关系

要启用此端口，请将 Number of inputs 参数设置为 Two inputs。

数据类型: single | double | fixed point

c — 相分量
标量

abc 参考系中三相系统的分量。

依存关系

要启用此端口，请将 Number of inputs 参数设置为 Two inputs。

数据类型: single | double | fixed point

abc — 相分量
标量

abc 参考系中三相系统的多路复用相分量 a、b 和 c。

依存关系

要启用此端口，请将 Number of inputs 参数设置为 Three inputs。

数据类型: single | double | fixed point

参数

全部展开

Number of inputs — 模块输入的数目
Two inputs (默认) | Three inputs

选择您可以指定的输入数目：

Two inputs - 将模块配置为接受两个单独的输入信号 α 和 β。该模块生成三个单独的输出信号 a、b 和 c。
Three inputs - 将模块配置为接受包含 α、β 和 0 信号的多路复用输入。该模块生成一个包含 a、b 和 c 信号的多路复用输出。

Power invariant — 启用功率不变性
`off` (默认) | `on`

要在模块输出中启用功率不变性属性，请选择此参数。要在模块输出中禁用功率不变性（启用振幅不变性），请不要选择此参数。

扩展功能

C/C++ 代码生成
使用 Simulink® Coder™ 生成 C 代码和 C++ 代码。

HDL 代码生成
使用 HDL Coder™ 为 FPGA 和 ASIC 设计生成 VHDL、Verilog 和 SystemVerilog 代码。

HDL Coder™ 提供了影响 HDL 实现和综合逻辑的额外配置选项。

HDL 架构

此模块具有一个默认 HDL 架构。

HDL 模块属性


ConstrainedOutputPipeline	要通过移动设计中的现有延迟来放置在输出端的寄存器的数量。分布式流水线不会重新分布这些寄存器。默认值为 `0`。有关更多详细信息，请参阅 ConstrainedOutputPipeline (HDL Coder)。
InputPipeline	要在生成的代码中插入的输入流水线阶段数。分布式流水线和受限输出流水线可以移动这些寄存器。默认值为 `0`。有关更多详细信息，请参阅 InputPipeline (HDL Coder)。
OutputPipeline	要在生成的代码中插入的输出流水线阶段数。分布式流水线和受限输出流水线可以移动这些寄存器。默认值为 `0`。有关更多详细信息，请参阅 OutputPipeline (HDL Coder)。

Inverse Clarke Transform

描述

方程

端口