Gain-Scheduled MPC Control of Nonlinear Chemical Reactor

About the Continuous Stirred Tank Reactor

A continuously stirred tank reactor (CSTR) is a common chemical system in the process industry. A schematic of the CSTR system is:

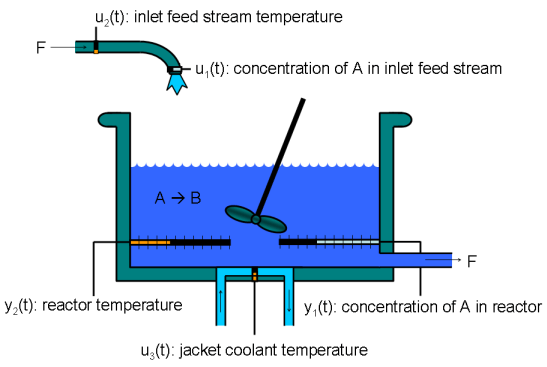
This system is a jacketed non-adiabatic tank reactor described extensively in [1]. The vessel is assumed to be perfectly mixed, and a single first-order exothermic and irreversible reaction, A --> B, takes place. The inlet stream of reagent A is fed to the tank at a constant volumetric rate. The product stream exits continuously at the same volumetric rate, and liquid density is constant. Thus, the volume of reacting liquid is constant.

The inputs of the CSTR model are:

The outputs of the model, which are also the model states, are:

The control objective is to maintain the concentration of reagent A, 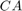at its desired setpoint, which changes over time when the reactor transitions from a low conversion rate to a high conversion rate. The coolant temperature 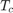is the manipulated variable used by the MPC controller to track the reference. The inlet feed stream concentration and temperature are assumed to be constant. The Simulink model mpc_cstr_plant implements the nonlinear CSTR plant.

About Gain-Scheduled Model Predictive Control

It is well known that the CSTR dynamics are strongly nonlinear with respect to reactor temperature variations and can be open-loop unstable during the transition from one operating condition to another. A single MPC controller designed at a particular operating condition cannot give satisfactory control performance over a wide operating range.

To control the nonlinear CSTR plant with linear MPC control technique, you have a few options:

(1) Design several MPC controllers offline, one for each plant model. At run time, use the Multiple MPC Controller block, which switches between controllers based on a desired scheduling strategy, as discussed in this example. Use this approach when the plant models have different orders or time delays.

(2) Design one MPC controller offline at a nominal operating point. At run time, use the Adaptive MPC Controller block together with a linear parameter-varying system (LPV System block). The Adaptive MPC Controller block updates the predictive model at each control interval, and the LPV System block supplies a linear plant model based on a scheduling strategy. For more details, see Adaptive MPC Control of Nonlinear Chemical Reactor Using Linear Parameter-Varying System. Use this approach when all the plant models have the same order and time delay.

(1) Use successive linearization. For more details, see Adaptive MPC Control of Nonlinear Chemical Reactor Using Successive Linearization. Use this approach when a nonlinear plant model is available and can be linearized at run time.

(2) Use online estimation to identify a linear model when loop is closed. For more details, see Adaptive MPC Control of Nonlinear Chemical Reactor Using Online Model Estimation. Use this approach when a linear plant model cannot be obtained from either an LPV system or successive linearization.

Obtain Linear Plant Model at Initial Operating Condition

To run this example, Simulink and Simulink Control Design™ software are required.

if ~mpcchecktoolboxinstalled('simulink')
    disp('Simulink is required to run this example.')
    return
end
if ~mpcchecktoolboxinstalled('slcontrol')
    disp('Simulink Control Design is required to run this example.')
    return
end

First, obtain a linear plant model at the initial operating condition, where CAi is 10 kgmol/m^3, and both Ti and Tc are 298.15 K. To generate the linear state-space system from the Simulink model, use functions such as operspec, findop, and linearize from Simulink Control Design.

Create operating point specification.

plant_mdl = 'mpc_cstr_plant';
op = operspec(plant_mdl);

Specify the known feed concentration at the initial condition.

op.Inputs(1).u = 10;
op.Inputs(1).Known = true;

Specify the known feed temperature at the initial condition.

op.Inputs(2).u = 298.15;
op.Inputs(2).Known = true;

Specify the known coolant temperature at the initial condition.

op.Inputs(3).u = 298.15;
op.Inputs(3).Known = true;

Compute the initial condition.

[op_point,op_report] = findop(plant_mdl,op);

 Operating point search report:
---------------------------------

opreport = 


 Operating point search report for the Model mpc_cstr_plant.
 (Time-Varying Components Evaluated at time t=0)

Operating point specifications were successfully met.
States: 
----------
    Min          x          Max        dxMin        dx         dxMax   
___________ ___________ ___________ ___________ ___________ ___________
                                                                       
(1.) mpc_cstr_plant/CSTR/Integrator
     0       311.2639       Inf          0      8.1176e-11       0     
(2.) mpc_cstr_plant/CSTR/Integrator1
     0        8.5698        Inf          0      -6.8709e-12      0     

Inputs: 
----------
 Min     u     Max  
______ ______ ______
                    
(1.) mpc_cstr_plant/CAi
  10     10     10  
(2.) mpc_cstr_plant/Ti
298.15 298.15 298.15
(3.) mpc_cstr_plant/Tc
298.15 298.15 298.15

Outputs: 
----------
  Min       y       Max   
________ ________ ________
                          
(1.) mpc_cstr_plant/T
  -Inf   311.2639   Inf   
(2.) mpc_cstr_plant/CA
  -Inf    8.5698    Inf   

Obtain nominal values of x, y, and u.

x0 = [op_report.States(1).x; op_report.States(2).x];
y0 = [op_report.Outputs(1).y; op_report.Outputs(2).y];
u0 = [op_report.Inputs(1).u; op_report.Inputs(2).u; op_report.Inputs(3).u];

Obtain a linear model at the initial condition.

plant = linearize(plant_mdl,op_point);

Verify that the linear model is open-loop stable at this condition.

eig(plant)

ans =

   -0.5223
   -0.8952

Design MPC Controller for Initial Operating Condition

Specify signal types used in MPC. Assume both reactor temperature and concentration are measurable.

plant.InputGroup.UnmeasuredDisturbances = [1 2];
plant.InputGroup.ManipulatedVariables = 3;
plant.OutputGroup.Measured = [1 2];
plant.InputName = {'CAi','Ti','Tc'};
plant.OutputName = {'T','CA'};

Create MPC controller with a specified sample time and default prediction and control horizons.

Ts = 0.5;
mpcobj = mpc(plant,Ts);

-->"PredictionHorizon" is empty. Assuming default 10.
-->"ControlHorizon" is empty. Assuming default 2.
-->"Weights.ManipulatedVariables" is empty. Assuming default 0.00000.
-->"Weights.ManipulatedVariablesRate" is empty. Assuming default 0.10000.
-->"Weights.OutputVariables" is empty. Assuming default 1.00000.
   for output(s) y1 and zero weight for output(s) y2 

Set nominal values in the controller. The nominal values for unmeasured disturbances must be zero.

mpcobj.Model.Nominal = struct('X',x0,'U',[0;0;u0(3)],'Y',y0,'DX',[0 0]);

Since the plant input and output signals have different orders of magnitude, specify scaling factors.

Uscale = [10;30;50];
Yscale = [50;10];
mpcobj.DV(1).ScaleFactor = Uscale(1);
mpcobj.DV(2).ScaleFactor = Uscale(2);
mpcobj.MV.ScaleFactor = Uscale(3);
mpcobj.OV(1).ScaleFactor = Yscale(1);
mpcobj.OV(2).ScaleFactor = Yscale(2);

The goal is to track a specified transition in the reactor concentration. The reactor temperature is measured and used in state estimation but the controller will not attempt to regulate it directly. It will vary as needed to regulate the concentration. Thus, set its MPC weight to zero.

mpcobj.Weights.OV = [0 1];

Plant inputs 1 and 2 are unmeasured disturbances. By default, the controller assumes integrated white noise with unit magnitude at these inputs when configuring the state estimator. Try increasing the state estimator signal-to-noise by a factor of 10 to improve disturbance rejection performance.

Dist = ss(getindist(mpcobj));
Dist.B = eye(2)*10;
setindist(mpcobj,'model',Dist);

-->Converting model to discrete time.
-->The "Model.Disturbance" property is empty:
   Assuming unmeasured input disturbance #1 is integrated white noise.
   Assuming unmeasured input disturbance #2 is integrated white noise.
   Assuming no disturbance added to measured output #2.
   Assuming no disturbance added to measured output #1.
-->"Model.Noise" is empty. Assuming white noise on each measured output.

Keep all other MPC parameters at their default values.

Test the Controller with a Step Disturbance in Feed Concentration

The mpc_cstr_single Simulink model contains the CSTR plant and MPC controller in a feedback configuration.

mpc_mdl = 'mpc_cstr_single';
open_system(mpc_mdl)

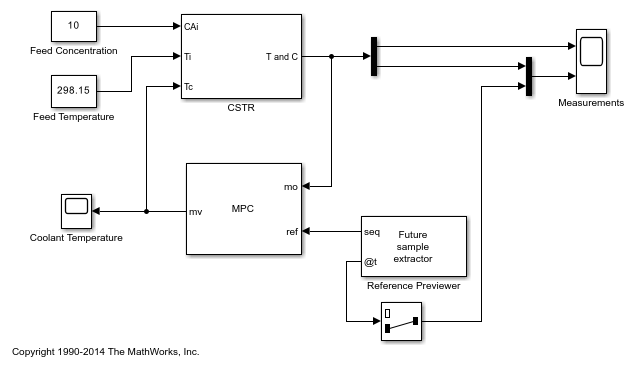
Note that the MPC Controller block is configured to look ahead at (preview) setpoint changes in the future; that is, anticipating the setpoint transition. This generally improves setpoint tracking.

Define a constant setpoint for the output.

CSTR_Setpoints.time = [0; 60];
CSTR_Setpoints.signals.values = [y0 y0]';

Test the response to a 5% increase in feed concentration.

set_param([mpc_mdl '/Feed Concentration'],'Value','10.5');

Set plot scales and simulate the response.

open_system([mpc_mdl '/Measurements'])
open_system([mpc_mdl '/Coolant Temperature'])
set_param([mpc_mdl '/Measurements'],'Ymin','305~8','Ymax','320~9')
set_param([mpc_mdl '/Coolant Temperature'],'Ymin','295','Ymax','305')
sim(mpc_mdl,10)

-->Converting model to discrete time.
   Assuming no disturbance added to measured output #2.
   Assuming no disturbance added to measured output #1.
-->"Model.Noise" is empty. Assuming white noise on each measured output.

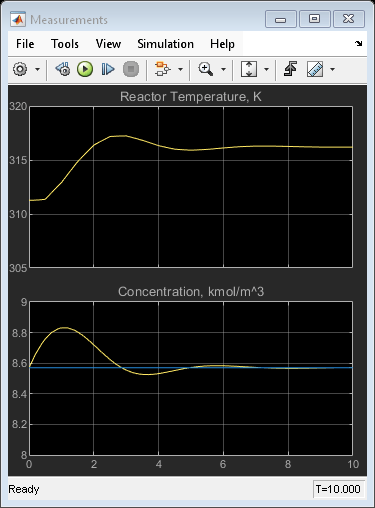
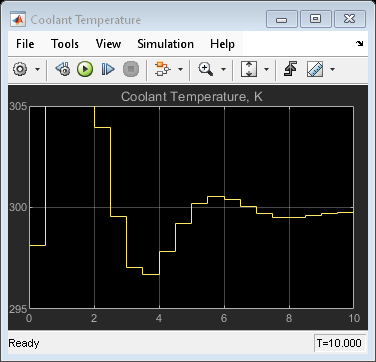
The closed-loop response is satisfactory.

Simulate Designed MPC Controller Using Full Transition

First, define the desired setpoint transition. After a 10-minute warm-up period, ramp the concentration setpoint downward at a rate of 0.25 per minute until it reaches 2.0 kmol/m^3.

CSTR_Setpoints.time = [0 10 11:39]';
CSTR_Setpoints.signals.values = [y0(1)*ones(31,1),[y0(2);y0(2);(y0(2):-0.25:2)';2;2]];

Remove the 5% increase in feed concentration used previously.

set_param([mpc_mdl '/Feed Concentration'],'Value','10')

Set plot scales and simulate the response.

set_param([mpc_mdl '/Measurements'],'Ymin','300~0','Ymax','400~10')
set_param([mpc_mdl '/Coolant Temperature'],'Ymin','240','Ymax','360')

Simulate the model.

sim(mpc_mdl,60)

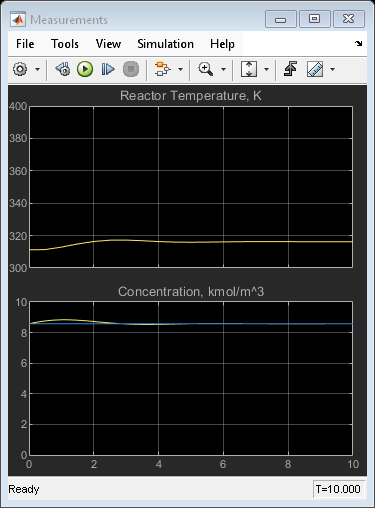
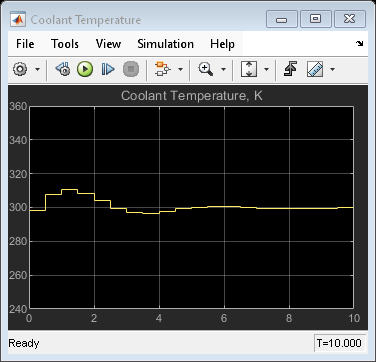
The closed-loop response is unacceptable. Performance along the full transition can be improved if other MPC controllers are designed at different operating conditions along the transition path. In the next two sections, you design MPC controllers for the intermediate and final transition stages.

Design MPC Controller for Intermediate Operating Condition

Create the operating point specification.

op = operspec(plant_mdl);

Specify the feed concentration.

op.Inputs(1).u = 10;
op.Inputs(1).Known = true;

Specify the feed temperature.

op.Inputs(2).u = 298.15;
op.Inputs(2).Known = true;

Specify the reactor concentration.

op.Outputs(2).y = 5.5;
op.Outputs(2).Known = true;

Find steady state operating condition.

[op_point,op_report] = findop(plant_mdl,op);

% Obtain nominal values of |x|, |y|, and |u|.
x0 = [op_report.States(1).x; op_report.States(2).x];
y0 = [op_report.Outputs(1).y; op_report.Outputs(2).y];
u0 = [op_report.Inputs(1).u; op_report.Inputs(2).u; op_report.Inputs(3).u];

 Operating point search report:
---------------------------------

opreport = 


 Operating point search report for the Model mpc_cstr_plant.
 (Time-Varying Components Evaluated at time t=0)

Operating point specifications were successfully met.
States: 
----------
    Min          x          Max        dxMin        dx         dxMax   
___________ ___________ ___________ ___________ ___________ ___________
                                                                       
(1.) mpc_cstr_plant/CSTR/Integrator
     0       339.4282       Inf          0      3.4187e-08       0     
(2.) mpc_cstr_plant/CSTR/Integrator1
     0          5.5         Inf          0      -2.8686e-09      0     

Inputs: 
----------
  Min      u      Max  
_______ _______ _______
                       
(1.) mpc_cstr_plant/CAi
  10      10      10   
(2.) mpc_cstr_plant/Ti
298.15  298.15  298.15 
(3.) mpc_cstr_plant/Tc
 -Inf   298.222   Inf  

Outputs: 
----------
  Min       y       Max   
________ ________ ________
                          
(1.) mpc_cstr_plant/T
  -Inf   339.4282   Inf   
(2.) mpc_cstr_plant/CA
  5.5      5.5      5.5   

Obtain a linear model at the initial condition.

plant_intermediate = linearize(plant_mdl,op_point);

Verify that the linear model is open-loop unstable at this condition.

eig(plant_intermediate)

ans =

    0.4941
   -0.8357

Specify signal types used in MPC. Assume both reactor temperature and concentration are measurable.

plant_intermediate.InputGroup.UnmeasuredDisturbances = [1 2];
plant_intermediate.InputGroup.ManipulatedVariables = 3;
plant_intermediate.OutputGroup.Measured = [1 2];
plant_intermediate.InputName = {'CAi','Ti','Tc'};
plant_intermediate.OutputName = {'T','CA'};

Create the MPC controller.

mpcobj_intermediate = mpc(plant_intermediate,Ts);

-->"PredictionHorizon" is empty. Assuming default 10.
-->"ControlHorizon" is empty. Assuming default 2.
-->"Weights.ManipulatedVariables" is empty. Assuming default 0.00000.
-->"Weights.ManipulatedVariablesRate" is empty. Assuming default 0.10000.
-->"Weights.OutputVariables" is empty. Assuming default 1.00000.
   for output(s) y1 and zero weight for output(s) y2 

Set nominal values, scaling factors, and weights in the controller.

mpcobj_intermediate.Model.Nominal = struct('X',x0,'U',[0;0;u0(3)],'Y',y0,'DX',[0 0]);
Uscale = [10;30;50];
Yscale = [50;10];
mpcobj_intermediate.DV(1).ScaleFactor = Uscale(1);
mpcobj_intermediate.DV(2).ScaleFactor = Uscale(2);
mpcobj_intermediate.MV.ScaleFactor = Uscale(3);
mpcobj_intermediate.OV(1).ScaleFactor = Yscale(1);
mpcobj_intermediate.OV(2).ScaleFactor = Yscale(2);
mpcobj_intermediate.Weights.OV = [0 1];
Dist = ss(getindist(mpcobj_intermediate));
Dist.B = eye(2)*10;
setindist(mpcobj_intermediate,'model',Dist);

-->Converting model to discrete time.
-->The "Model.Disturbance" property is empty:
   Assuming unmeasured input disturbance #1 is integrated white noise.
   Assuming unmeasured input disturbance #2 is integrated white noise.
   Assuming no disturbance added to measured output #2.
   Assuming no disturbance added to measured output #1.
-->"Model.Noise" is empty. Assuming white noise on each measured output.

Design MPC Controller for Final Operating Condition

Create the operating point specification.

op = operspec(plant_mdl);

Specify the feed concentration.

op.Inputs(1).u = 10;
op.Inputs(1).Known = true;

Specify the feed temperature.

op.Inputs(2).u = 298.15;
op.Inputs(2).Known = true;

Specify the reactor concentration.

op.Outputs(2).y = 2;
op.Outputs(2).Known = true;

Find steady-state operating condition.

[op_point,op_report] = findop(plant_mdl,op);

% Obtain nominal values of |x|, |y|, and |u|.
x0 = [op_report.States(1).x; op_report.States(2).x];
y0 = [op_report.Outputs(1).y; op_report.Outputs(2).y];
u0 = [op_report.Inputs(1).u; op_report.Inputs(2).u; op_report.Inputs(3).u];

 Operating point search report:
---------------------------------

opreport = 


 Operating point search report for the Model mpc_cstr_plant.
 (Time-Varying Components Evaluated at time t=0)

Operating point specifications were successfully met.
States: 
----------
    Min          x          Max        dxMin        dx         dxMax   
___________ ___________ ___________ ___________ ___________ ___________
                                                                       
(1.) mpc_cstr_plant/CSTR/Integrator
     0       373.1311       Inf          0      5.7298e-11       0     
(2.) mpc_cstr_plant/CSTR/Integrator1
     0           2          Inf          0      -4.7411e-12      0     

Inputs: 
----------
  Min       u       Max   
________ ________ ________
                          
(1.) mpc_cstr_plant/CAi
   10       10       10   
(2.) mpc_cstr_plant/Ti
 298.15   298.15   298.15 
(3.) mpc_cstr_plant/Tc
  -Inf   305.2015   Inf   

Outputs: 
----------
  Min       y       Max   
________ ________ ________
                          
(1.) mpc_cstr_plant/T
  -Inf   373.1311   Inf   
(2.) mpc_cstr_plant/CA
   2        2        2    

Obtain a linear model at the initial condition.

plant_final = linearize(plant_mdl,op_point);

Verify that the linear model is again open-loop stable at this condition.

eig(plant_final)

ans =

  -1.1077 + 1.0901i
  -1.1077 - 1.0901i

Specify signal types used in MPC. Assume both reactor temperature and concentration are measurable.

plant_final.InputGroup.UnmeasuredDisturbances = [1 2];
plant_final.InputGroup.ManipulatedVariables = 3;
plant_final.OutputGroup.Measured = [1 2];
plant_final.InputName = {'CAi','Ti','Tc'};
plant_final.OutputName = {'T','CA'};

Create the MPC controller.

mpcobj_final = mpc(plant_final,Ts);

-->"PredictionHorizon" is empty. Assuming default 10.
-->"ControlHorizon" is empty. Assuming default 2.
-->"Weights.ManipulatedVariables" is empty. Assuming default 0.00000.
-->"Weights.ManipulatedVariablesRate" is empty. Assuming default 0.10000.
-->"Weights.OutputVariables" is empty. Assuming default 1.00000.
   for output(s) y1 and zero weight for output(s) y2 

Set nominal values, scaling factors, and weights in the controller.

mpcobj_final.Model.Nominal = struct('X',x0,'U',[0;0;u0(3)],'Y',y0,'DX',[0 0]);
Uscale = [10;30;50];
Yscale = [50;10];
mpcobj_final.DV(1).ScaleFactor = Uscale(1);
mpcobj_final.DV(2).ScaleFactor = Uscale(2);
mpcobj_final.MV.ScaleFactor = Uscale(3);
mpcobj_final.OV(1).ScaleFactor = Yscale(1);
mpcobj_final.OV(2).ScaleFactor = Yscale(2);
mpcobj_final.Weights.OV = [0 1];
Dist = ss(getindist(mpcobj_final));
Dist.B = eye(2)*10;
setindist(mpcobj_final,'model',Dist);

-->Converting model to discrete time.
-->The "Model.Disturbance" property is empty:
   Assuming unmeasured input disturbance #1 is integrated white noise.
   Assuming unmeasured input disturbance #2 is integrated white noise.
   Assuming no disturbance added to measured output #2.
   Assuming no disturbance added to measured output #1.
-->"Model.Noise" is empty. Assuming white noise on each measured output.

Control CSTR Plant Using Multiple MPC Controllers

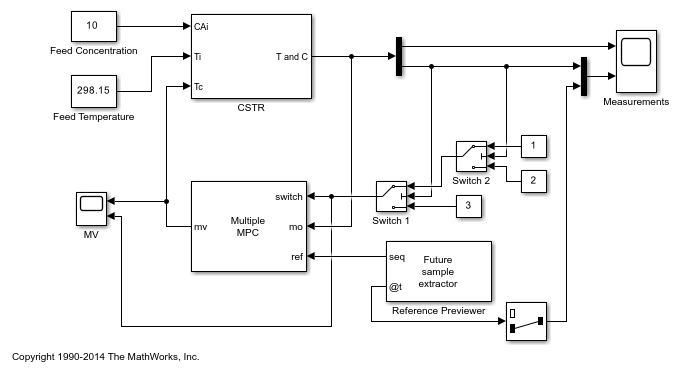
The following model uses the Multiple MPC Controllers block to implement three MPC controllers across the operating range.

mmpc_mdl = 'mpc_cstr_multiple';
open_system(mmpc_mdl)

The model is configured to use the three controllers in a sequence: mpcobj, mpcobj_intermediate, and mpcobj_final.

open_system([mmpc_mdl '/Multiple MPC Controllers'])

Also, the two switches specify when to switch from one controller to another. The rules are:

Simulate using the Multiple MPC Controllers block.

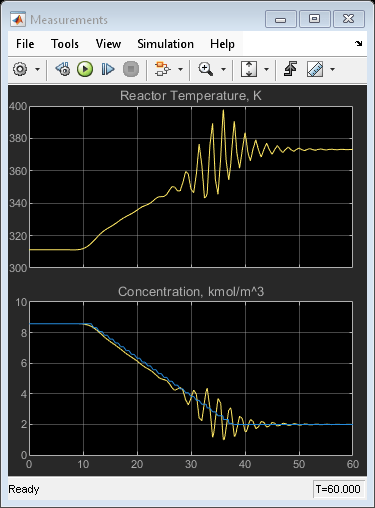
open_system([mmpc_mdl '/Measurements'])
open_system([mmpc_mdl '/MV'])
sim(mmpc_mdl)

-->Converting model to discrete time.
   Assuming no disturbance added to measured output #2.
   Assuming no disturbance added to measured output #1.
-->"Model.Noise" is empty. Assuming white noise on each measured output.
-->Converting model to discrete time.
   Assuming no disturbance added to measured output #2.
   Assuming no disturbance added to measured output #1.
-->"Model.Noise" is empty. Assuming white noise on each measured output.

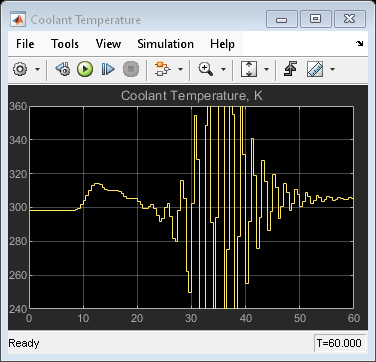
The transition is now well-controlled. The major improvement is in the transition through the open-loop unstable region. The plot of the switching signal shows when controller transitions occur. The MV character changes at these times because of the change in dynamic characteristics introduced by the new prediction model.

References

[1] Seborg, D. E., T. F. Edgar, and D. A. Mellichamp, Process Dynamics and Control, 2nd Edition, Wiley, 2004.

bdclose(plant_mdl)
bdclose(mpc_mdl)
bdclose(mmpc_mdl)