Rotations, Orientation, and Quaternions
This example reviews concepts in three-dimensional rotations and how quaternions are used to describe orientation and rotations. Quaternions are a skew field of hypercomplex numbers. They have found applications in aerospace, computer graphics, and virtual reality. In MATLAB®, quaternion mathematics can be represented by manipulating the quaternion class.
The HelperDrawRotation class is used to illustrate several portions of this example.
dr = HelperDrawRotation;
Rotations in Three Dimensions
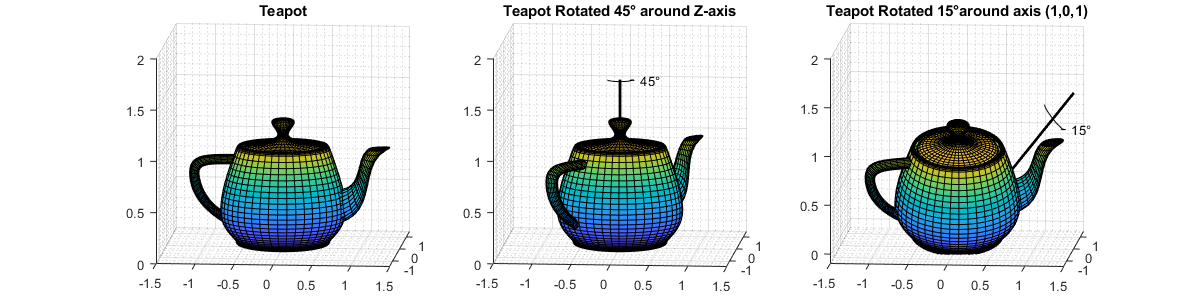
All rotations in 3-D can be defined by an axis of rotation and an angle of rotation about that axis. Consider the 3-D image of a teapot in the leftmost plot. The teapot is rotated by 45 degrees around the Z-axis in the second plot. A more complex rotation of 15 degrees around the axis [1 0 1] is shown in the third plot. Quaternions encapsulate the axis and angle of rotation and have an algebra for manipulating these rotations. The quaternion class, and this example, use the "right-hand rule" convention to define rotations. That is, positive rotations are clockwise around the axis of rotation when viewed from the origin.
dr.drawTeapotRotations;
Point Rotation
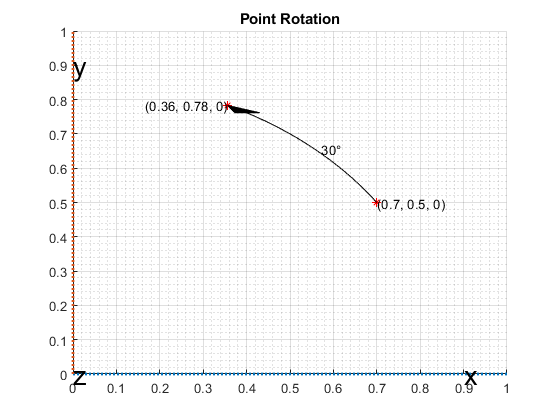
The vertices of the teapot were rotated about the axis of rotation in the reference frame. Consider a point (0.7, 0.5) rotated 30 degrees about the Z-axis.
figure; dr.draw2DPointRotation(gca);
Frame Rotation
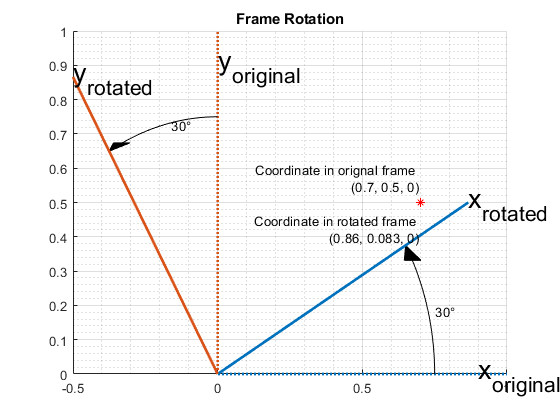
Frame rotation is, in some sense, the opposite of point rotation. In frame rotation, the points of the object stay fixed, but the frame of reference is rotated. Again, consider the point (0.7, 0.5). Now the reference frame is rotated by 30 degrees around the Z-axis. Note that while the point (0.7, 0.5) stays fixed, it has different coordinates in the new, rotated frame of reference.
figure; dr.draw2DFrameRotation(gca);
Orientation
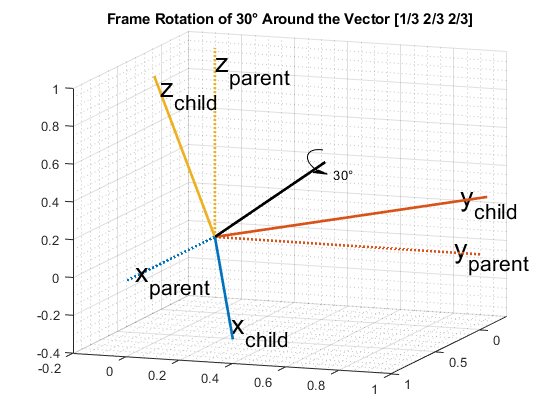
Orientation refers to the angular displacement of an object relative to a frame of reference. Typically, orientation is described by the rotation that causes this angular displacement from a starting orientation. In this example, orientation is defined as the rotation that takes a quantity in a parent reference frame to a child reference frame. Orientation is usually given as a quaternion, rotation matrix, set of Euler angles, or rotation vector. It is useful to think about orientation as a frame rotation: the child reference frame is rotated relative to the parent frame.
Consider an example where the child reference frame is rotated 30 degrees around the vector [1/3 2/3 2/3].
figure; dr.draw3DOrientation(gca, [1/3 2/3 2/3], 30);
Quaternions
Quaternions are numbers of the form
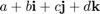
where
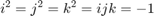
and 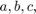 and
and  are real numbers. In the rest of this example, the four numbers
are real numbers. In the rest of this example, the four numbers 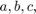 and
and  are referred to as the parts of the quaternion.
are referred to as the parts of the quaternion.
Quaternions for Rotations and Orientation
The axis and the angle of rotation are encapsulated in the quaternion parts. For a unit vector axis of rotation [ x, y, z], and rotation angle  , the quaternion describing this rotation is
, the quaternion describing this rotation is

Note that to describe a rotation using a quaternion, the quaternion must be a unit quaternion. A unit quaternion has a norm of 1, where the norm is defined as
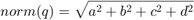
There are a variety of ways to construct a quaternion in MATLAB, for example:
q1 = quaternion(1,2,3,4)
q1 =
quaternion
1 + 2i + 3j + 4k
Arrays of quaternions can be made in the same way:
quaternion([1 10; -1 1], [2 20; -2 2], [3 30; -3 3], [4 40; -4 4])
ans =
2×2 quaternion array
1 + 2i + 3j + 4k 10 + 20i + 30j + 40k
-1 - 2i - 3j - 4k 1 + 2i + 3j + 4k
Arrays with four columns can also be used to construct quaternions, with each column representing a quaternion part:
qmgk = quaternion(magic(4))
qmgk =
4×1 quaternion array
16 + 2i + 3j + 13k
5 + 11i + 10j + 8k
9 + 7i + 6j + 12k
4 + 14i + 15j + 1k
Quaternions can be indexed and manipulated just like any other array:
qmgk(3)
ans =
quaternion
9 + 7i + 6j + 12k
reshape(qmgk,2,2)
ans =
2×2 quaternion array
16 + 2i + 3j + 13k 9 + 7i + 6j + 12k
5 + 11i + 10j + 8k 4 + 14i + 15j + 1k
[q1; q1]
ans =
2×1 quaternion array
1 + 2i + 3j + 4k
1 + 2i + 3j + 4k
Quaternion Math
Quaternions have well-defined arithmetic operations. Addition and subtraction are similar to complex numbers: parts are added/subtracted independently. Multiplication is more complicated because of the earlier equation:
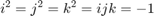
This means that multiplication of quaternions is not commutative. That is,  for quaternions
for quaternions 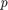 and
and  . However, every quaternion has a multiplicative inverse, so quaternions can be divided. Arrays of the
. However, every quaternion has a multiplicative inverse, so quaternions can be divided. Arrays of the quaternion class can be added, subtracted, multiplied, and divided in MATLAB.
q = quaternion(1,2,3,4); p = quaternion(-5,6,-7,8);
Addition
p + q
ans =
quaternion
-4 + 8i - 4j + 12k
Subtraction
p - q
ans =
quaternion
-6 + 4i - 10j + 4k
Multiplication
p*q
ans =
quaternion
-28 - 56i - 30j + 20k
Multiplication in the reverse order (note the different result)
q*p
ans =
quaternion
-28 + 48i - 14j - 44k
Right division of p by q is equivalent to 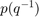 .
.
p./q
ans =
quaternion
0.6 + 2.2667i + 0.53333j - 0.13333k
Left division of q by p is equivalent to 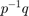 .
.
p.\q
ans =
quaternion
0.10345 + 0.2069i + 0j - 0.34483k
The conjugate of a quaternion is formed by negating each of the non-real parts, similar to conjugation for a complex number:
conj(p)
ans =
quaternion
-5 - 6i + 7j - 8k
Quaternions can be normalized in MATLAB:
pnormed = normalize(p)
pnormed =
quaternion
-0.37905 + 0.45486i - 0.53067j + 0.60648k
norm(pnormed)
ans =
1
Point and Frame Rotations with Quaternions
Quaternions can be used to rotate points in a static frame of reference, or to rotate the frame of reference itself. The rotatepoint function rotates a point 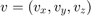 using a quaternion
using a quaternion  through the following equation:
through the following equation:

where 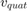 is
is
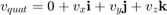
and 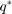 indicates quaternion conjugation. Note the above quaternion multiplication results in a quaternion with the real part,
indicates quaternion conjugation. Note the above quaternion multiplication results in a quaternion with the real part,  , equal to 0. The
, equal to 0. The 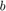 ,
,  , and
, and  parts of the result form the rotated point (
parts of the result form the rotated point (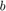 ,
,  ,
,  ).
).
Consider the example of point rotation from above. The point (0.7, 0.5) was rotated 30 degrees around the Z-axis. In three dimensions this point has a 0 Z-coordinate. Using the axis-angle formulation, a quaternion can be constructed using [0 0 1] as the axis of rotation.
ang = deg2rad(30);
q = quaternion(cos(ang/2), 0, 0, sin(ang/2));
pt = [0.7, 0.5, 0]; % Z-coordinate is 0 in the X-Y plane
ptrot = rotatepoint(q, pt)
ptrot =
0.3562 0.7830 0
Similarly, the rotateframe function takes a quaternion  and point
and point  to compute
to compute

Again the above quaternion multiplication results in a quaternion with 0 real part. The (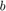 ,
,  ,
,  ) parts of the result form the coordinate of the point
) parts of the result form the coordinate of the point  in the new, rotated reference frame. Using the
in the new, rotated reference frame. Using the quaternion class:
ptframerot = rotateframe(q, pt)
ptframerot =
0.8562 0.0830 0
A quaternion and its conjugate have opposite effects because of the symmetry in the point and frame rotation equations. Rotating by the conjugate "undoes" the rotation.
rotateframe(conj(q), ptframerot)
ans =
0.7000 0.5000 0
Because of the symmetry of the equations, this code performs the same rotation.
rotatepoint(q, ptframerot)
ans =
0.7000 0.5000 0
Other Rotation Representations
Often rotations and orientations are described using alternate means: Euler angles, rotation matrices, and/or rotation vectors. All of these interoperate with quaternions in MATLAB.
Euler angles are frequently used because they are easy to interpret. Consider a frame of reference rotated by 30 degrees around the Z-axis, then 20 degrees around the Y-axis, and then -50 degrees around the X-axis. Note here, and throughout, the rotations around each axis are intrinsic: each subsequent rotation is around the newly created set of axes. In other words, the second rotation is around the "new" Y-axis created by the first rotation, not around the original Y-axis.
figure; euld = [30 20 -50]; dr.drawEulerRotation(gca, euld);

To build a quaternion from these Euler angles for the purpose of frame rotation, use the quaternion constructor. Since the order of rotations is around the Z-axis first, then around the new Y-axis, and finally around the new X-axis, use the 'ZYX' flag.
qeul = quaternion(deg2rad(euld), 'euler', 'ZYX', 'frame')
qeul =
quaternion
0.84313 - 0.44275i + 0.044296j + 0.30189k
The 'euler' flag indicates that the first argument is in radians. If the argument is in degrees, use the 'eulerd' flag.
qeuld = quaternion(euld, 'eulerd', 'ZYX', 'frame')
qeuld =
quaternion
0.84313 - 0.44275i + 0.044296j + 0.30189k
To convert back to Euler angles:
rad2deg(euler(qeul, 'ZYX', 'frame'))
ans = 30.0000 20.0000 -50.0000
Equivalently, the eulerd method can be used.
eulerd(qeul, 'ZYX', 'frame')
ans = 30.0000 20.0000 -50.0000
Alternatively, this same rotation can be represented as a rotation matrix:
rmat = rotmat(qeul, 'frame')
rmat =
0.8138 0.4698 -0.3420
-0.5483 0.4257 -0.7198
-0.1926 0.7733 0.6040
The conversion back to quaternions is similar:
quaternion(rmat, 'rotmat', 'frame')
ans =
quaternion
0.84313 - 0.44275i + 0.044296j + 0.30189k
Just as a quaternion can be used for either point or frame rotation, it can be converted to a rotation matrix (or set of Euler angles) specifically for point or frame rotation. The rotation matrix for point rotation is the transpose of the matrix for frame rotation. To convert between rotation representations, it is necessary to specify 'point' or 'frame'.
The rotation matrix for the point rotation section of this example is:
rotmatPoint = rotmat(q, 'point')
rotmatPoint =
0.8660 -0.5000 0
0.5000 0.8660 0
0 0 1.0000
To find the location of the rotated point, right-multiply rotmatPoint by the transposed array pt.
rotmatPoint * (pt')
ans =
0.3562
0.7830
0
The rotation matrix for the frame rotation section of this example is:
rotmatFrame = rotmat(q, 'frame')
rotmatFrame =
0.8660 0.5000 0
-0.5000 0.8660 0
0 0 1.0000
To find the location of the point in the rotated reference frame, right-multiply rotmatFrame by the transposed array pt.
rotmatFrame * (pt')
ans =
0.8562
0.0830
0
A rotation vector is an alternate, compact rotation encapsulation. A rotation vector is simply a three-element vector that represents the unit length axis of rotation scaled-up by the angle of rotation in radians. There is no frame-ness or point-ness associated with a rotation vector. To convert to a rotation vector:
rv = rotvec(qeul)
rv = -0.9349 0.0935 0.6375
To convert to a quaternion:
quaternion(rv, 'rotvec')
ans =
quaternion
0.84313 - 0.44275i + 0.044296j + 0.30189k
Distance
One advantage of quaternions over Euler angles is the lack of discontinuities. Euler angles have discontinuities that vary depending on the convention being used. The dist function compares the effect of rotation by two different quaternions. The result is a number in the range of 0 to pi. Consider two quaternions constructed from Euler angles:
eul1 = [0, 10, 0]; eul2 = [0, 15, 0]; qdist1 = quaternion(deg2rad(eul1), 'euler', 'ZYX', 'frame'); qdist2 = quaternion(deg2rad(eul2), 'euler', 'ZYX', 'frame');
Subtracting the Euler angles, you can see there is no rotation around the Z-axis or X-axis.
eul2 - eul1
ans =
0 5 0
The difference between these two rotations is five degrees around the Y-axis. The dist shows the difference as well.
rad2deg(dist(qdist1, qdist2))
ans =
5.0000
For Euler angles such as eul1 and eul2, computing angular distance is trivial. A more complex example, which spans an Euler angle discontinuity, is:
eul3 = [0, 89, 0]; eul4 = [180, 89, 180]; qdist3 = quaternion(deg2rad(eul3), 'euler', 'ZYX', 'frame'); qdist4 = quaternion(deg2rad(eul4), 'euler', 'ZYX', 'frame');
Though eul3 and eul4 represent nearly the same orientation, simple Euler angle subtraction gives the impression that these two orientations are very far apart.
euldiff = eul4 - eul3
euldiff = 180 0 180
Using the dist function on the quaternions shows that there is only a two-degree difference in these rotations:
euldist = rad2deg(dist(qdist3, qdist4))
euldist =
2.0000
A quaternion and its negative represent the same rotation. This is not obvious from subtracting quaternions, but the dist function makes it clear.
qpos = quaternion(-cos(pi/4), 0 ,0, sin(pi/4))
qpos =
quaternion
-0.70711 + 0i + 0j + 0.70711k
qneg = -qpos
qneg =
quaternion
0.70711 + 0i + 0j - 0.70711k
qdiff = qpos - qneg
qdiff =
quaternion
-1.4142 + 0i + 0j + 1.4142k
dist(qpos, qneg)
ans =
0
Supported Functions
The quaternion class lets you effectively describe rotations and orientations in MATLAB. The full list of quaternion-supported functions can be found with the methods function:
methods('quaternion')
Methods for class quaternion: angvel ismatrix power cat isnan prod classUnderlying isrow quaternion compact isscalar rdivide conj isvector reshape ctranspose ldivide rotateframe disp length rotatepoint dist log rotmat double meanrot rotvec eq minus rotvecd euler mldivide single eulerd mrdivide size exp mtimes slerp horzcat ndims times interp1 ne transpose iscolumn norm uminus isempty normalize underlyingType isequal numel validateattributes isequaln parts vertcat isfinite permute isinf plus Static methods: nan zeros ones