工厂、仓库、销售分配模型：基于求解器

此示例显示如何建立和求解混合整数线性规划问题。问题是在一组工厂、仓库和销售网点中找到最佳的生产和分销水平。有关基于问题的方法，请参阅工厂、仓库、销售分配模型：基于问题。

该示例首先为工厂、仓库和销售网点生成随机位置。请随意修改缩放参数 $N$ ，它不仅缩放生产和分销设施所在网格的大小，还缩放这些设施的数量，使得每个网格区域每种类型的设施密度与 $N$ 无关。

设施位置

对于缩放参数 $N$ 的给定值，假设存在以下内容：

$⌊ f N^{2} ⌋$ 工厂
$⌊ w N^{2} ⌋$ 仓库
$⌊ s N^{2} ⌋$ 销售网点

这些设施位于 $N$ 和 $x$ 方向 1 至 $y$ 之间的单独整数网格点上。为了使设施有单独的位置，您需要 $f + w + s \leq 1$ 。在此示例中，取 $N = 20$ 、 $f = 0.05$ 、 $w = 0.05$ 和 $s = 0.1$ 。

生产和发行

有工厂生产 $P$ 种产品。取 $P = 20$ 。

销售网点 $p$ 中每种产品 $s$ 的需求量为 $d (s, p)$ 。需求是在一定时间间隔内可以销售的数量。该模型的一个约束是需求得到满足，这意味着系统生产和分配的数量恰好是需求的数量。

每个工厂和每个仓库都有容量约束。

工厂 $p$ 生产的产品 $f$ 少于 $p c a p (f, p)$ 。
仓库 $w$ 的容量为 $w c a p (w)$ 。
在时间间隔内可以从仓库 $p$ 运输到销售网点的产品 $w$ 的数量小于 $t u r n (p) * w c a p (w)$ ，其中 $t u r n (p)$ 是产品 $p$ 的周转率。

假设每个销售网点仅从一个仓库接收供货。问题的一部分是确定销售网点到仓库的最便宜的映射。

成本

将产品从工厂运输到仓库，以及从仓库运输到销售网点的成本取决于设施之间的距离以及具体产品。如果 $d i s t (a, b)$ 是设施 $a$ 和 $b$ 之间的距离，那么在这两个设施之间运送产品 $p$ 的成本就是距离乘以运输成本 $t c o s t (p)$ ：

$d i s t (a, b) * t c o s t (p) .$

本例中的距离是网格距离，也称为 $L_{1}$ 距离。它是 $x$ 坐标和 $y$ 坐标的绝对差的总和。

工厂 $p$ 生产一单位产品 $f$ 的成本为 $p c o s t (f, p)$ 。

优化问题

给定一组设施位置以及需求和容量约束，找到：

每个工厂每种产品的生产水平
产品从工厂到仓库的配送时间表
产品从仓库到销售网点的配送时间表

这些数量必须确保满足需求并且总成本最小化。此外，每个销售网点都必须从一个仓库接收所有产品。

优化问题的变量和方程

控制变量，也就是您可以在优化中改变的变量，是

$x (p, f, w)$ = 从工厂 $p$ 运输到仓库 $f$ 的产品 $w$ 的数量
$y (s, w)$ = 二元变量，当销售网点 $s$ 与仓库 $w$ 关联时，取值为 1

要最小化的目标函数是

$\sum_{f} \sum_{p} \sum_{w} x (p, f, w) \cdot (p c o s t (f, p) + t c o s t (p) \cdot d i s t (f, w))$

$+ \sum_{s} \sum_{w} \sum_{p} (d (s, p) \cdot t c o s t (p) \cdot d i s t (s, w) \cdot y (s, w)) .$

约束包括

$\sum_{w} x (p, f, w) \leq p c a p (f, p)$ （工厂产能）。

$\sum_{f} x (p, f, w) = \sum_{s} (d (s, p) \cdot y (s, w))$ （需求得到满足）。

$\sum_{p} \sum_{s} \frac{d (s, p)}{t u r n (p)} \cdot y (s, w) \leq w c a p (w)$ （仓库容量）。

$\sum_{w} y (s, w) = 1$ （每个销售网点与一个仓库关联）。

$x (p, f, w) \geq 0$ （非负产量）。

$y (s, w) ϵ {0, 1}$ （二元变量 $y$ ）。

变量 $x$ 和 $y$ 线性出现在目标函数和约束函数中。由于 $y$ 仅限于整数值，因此该问题是混合整数线性规划 (MILP)。

生成随机问题：设施位置

设置 $N$ 、 $f$ 、 $w$ 、 $s$ 参数的值，并生成设施位置。

rng(1) % for reproducibility
N = 20; % N from 10 to 30 seems to work. Choose large values with caution.
N2 = N*N;
f = 0.05; % density of factories
w = 0.05; % density of warehouses
s = 0.1; % density of sales outlets

F = floor(f*N2); % number of factories
W = floor(w*N2); % number of warehouses
S = floor(s*N2); % number of sales outlets

xyloc = randperm(N2,F+W+S); % unique locations of facilities
[xloc,yloc] = ind2sub([N N],xyloc);

当然，设施随意选址是不现实的。此示例旨在展示解技术，而不是如何生成良好的设施位置。

绘制设施。设施 1 至 F 为工厂，F+1 至 F+W 为仓库，F+W+1 至 F+W+S 为销售网点。

h = figure;
plot(xloc(1:F),yloc(1:F),'rs',xloc(F+1:F+W),yloc(F+1:F+W),'k*',...
    xloc(F+W+1:F+W+S),yloc(F+W+1:F+W+S),'bo');
lgnd = legend('Factory','Warehouse','Sales outlet','Location','EastOutside');
lgnd.AutoUpdate = 'off';
xlim([0 N+1]);ylim([0 N+1])

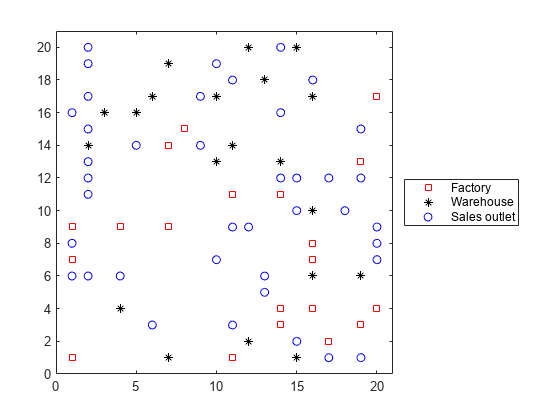
Figure contains an axes object. The axes object contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent Factory, Warehouse, Sales outlet.

生成随机容量、成本和需求

生成随机生产成本、产能、周转率和需求。

P = 20; % 20 products

% Production costs between 20 and 100
pcost = 80*rand(F,P) + 20;

% Production capacity between 500 and 1500 for each product/factory
pcap = 1000*rand(F,P) + 500;

% Warehouse capacity between P*400 and P*800 for each product/warehouse
wcap = P*400*rand(W,1) + P*400;

% Product turnover rate between 1 and 3 for each product
turn = 2*rand(1,P) + 1;

% Product transport cost per distance between 5 and 10 for each product
tcost = 5*rand(1,P) + 5;

% Product demand by sales outlet between 200 and 500 for each
% product/outlet
d = 300*rand(S,P) + 200;

这些随机的需求和能力可能会导致不可行的问题。换句话说，有时需求超出了生产和仓库容量的约束。如果您改变某些参数并得到一个不可行的问题，在解中您将得到一个 -2 的退出标志。

生成目标和约束矩阵和向量

obj 中的目标函数向量 intlincon 由变量 $x (p, f, w)$ 和 $y (s, w)$ 的系数组成。因此 P*F*W + S*W 中自然存在 obj 系数。

生成系数的一种方法是首先为 $x$ 系数生成一个 P-by-F-by-W 数组 obj1，然后为 $y (s, w)$ 系数生成一个 S-by-W 数组 obj2。然后将这些数组转换为两个向量，并通过调用将它们组合成 obj

obj = [obj1(:);obj2(:)];

obj1 = zeros(P,F,W); % Allocate arrays
obj2 = zeros(S,W);

在目标和约束向量和矩阵的生成中，我们生成 $(p, f, w)$ 数组或 $(s, w)$ 数组，然后将结果转换为向量。

要开始生成输入，请生成距离数组 distfw(i,j) 和 distsw(i,j)。

distfw = zeros(F,W); % Allocate matrix for factory-warehouse distances
for ii = 1:F
    for jj = 1:W
        distfw(ii,jj) = abs(xloc(ii) - xloc(F + jj)) + abs(yloc(ii) ...
            - yloc(F + jj));
    end
end

distsw = zeros(S,W); % Allocate matrix for sales outlet-warehouse distances
for ii = 1:S
    for jj = 1:W
        distsw(ii,jj) = abs(xloc(F + W + ii) - xloc(F + jj)) ...
            + abs(yloc(F + W + ii) - yloc(F + jj));
    end
end

生成 obj1 和 obj2 的条目。

for ii = 1:P
    for jj = 1:F
        for kk = 1:W
            obj1(ii,jj,kk) = pcost(jj,ii) + tcost(ii)*distfw(jj,kk);
        end
    end
end

for ii = 1:S
    for jj = 1:W
        obj2(ii,jj) = distsw(ii,jj)*sum(d(ii,:).*tcost);
    end
end

将条目合并为一个向量。

obj = [obj1(:);obj2(:)]; % obj is the objective function vector

现在创建约束矩阵。

每个线性约束矩阵的宽度是 obj 向量的长度。

matwid = length(obj);

线性不等式有两种类型：生产能力约束和仓库容量约束。

有 P*F 生产能力的约束，也有 W 仓库容量的约束。约束矩阵非常稀疏，非零值的数量级为 1%，因此使用稀疏矩阵可以节省内存。

Aineq = spalloc(P*F + W,matwid,P*F*W + S*W); % Allocate sparse Aeq
bineq = zeros(P*F + W,1); % Allocate bineq as full

% Zero matrices of convenient sizes:
clearer1 = zeros(size(obj1));
clearer12 = clearer1(:);
clearer2 = zeros(size(obj2));
clearer22 = clearer2(:);

% First the production capacity constraints
counter = 1;
for ii = 1:F
    for jj = 1:P
        xtemp = clearer1;
        xtemp(jj,ii,:) = 1; % Sum over warehouses for each product and factory
        xtemp = sparse([xtemp(:);clearer22]); % Convert to sparse
        Aineq(counter,:) = xtemp'; % Fill in the row
        bineq(counter) = pcap(ii,jj);
        counter = counter + 1;
    end
end

% Now the warehouse capacity constraints
vj = zeros(S,1); % The multipliers 
for jj = 1:S
    vj(jj) = sum(d(jj,:)./turn); % A sum of P elements
end

for ii = 1:W
    xtemp = clearer2;
    xtemp(:,ii) = vj;
    xtemp = sparse([clearer12;xtemp(:)]); % Convert to sparse
    Aineq(counter,:) = xtemp'; % Fill in the row
    bineq(counter) = wcap(ii);
    counter = counter + 1;
end

线性等式约束有两种类型：满足需求的约束和每个销售网点对应一个仓库的约束。

Aeq = spalloc(P*W + S,matwid,P*W*(F+S) + S*W); % Allocate as sparse
beq = zeros(P*W + S,1); % Allocate vectors as full

counter = 1;
% Demand is satisfied:
for ii = 1:P
    for jj = 1:W
        xtemp = clearer1;
        xtemp(ii,:,jj) = 1;
        xtemp2 = clearer2;
        xtemp2(:,jj) = -d(:,ii);
        xtemp = sparse([xtemp(:);xtemp2(:)]'); % Change to sparse row
        Aeq(counter,:) = xtemp; % Fill in row
        counter = counter + 1;
    end
end

% Only one warehouse for each sales outlet:
for ii = 1:S
    xtemp = clearer2;
    xtemp(ii,:) = 1;
    xtemp = sparse([clearer12;xtemp(:)]'); % Change to sparse row
    Aeq(counter,:) = xtemp; % Fill in row
    beq(counter) = 1;
    counter = counter + 1;
end

边界约束和整数变量

整数变量是从 length(obj1) + 1 到末尾的变量。

intcon = P*F*W+1:length(obj);

上界也是从 length(obj1) + 1 到末尾。

lb = zeros(length(obj),1);
ub = Inf(length(obj),1);
ub(P*F*W+1:end) = 1;

关闭迭代显示，这样您就不会得到数百行输出。包括一个绘图函数来监控解的进度。

opts = optimoptions("intlinprog",Display="off",...
    PlotFcn=@optimplotmilp);

求解问题

您生成了所有求解器输入。调用求解器来寻找解。

[solution,fval,exitflag,output] = intlinprog(obj,intcon,...
                                     Aineq,bineq,Aeq,beq,lb,ub,opts);

Figure Optimization Plot Function contains an axes object. The axes object with title Best Objective: 3.0952e+07, Relative Gap: 7.60069e-06, xlabel Number of nodes, ylabel Objective value contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent Primal bound, Dual bound, New solution.

if isempty(solution) % If the problem is infeasible or you stopped early with no solution
    disp('intlinprog did not return a solution.')
    return % Stop the script because there is nothing to examine
end

检查解

该解是可行的，在给定的公差范围内。

exitflag

exitflag = 
1

infeas1 = max(Aineq*solution - bineq)

infeas1 = 
8.4128e-12

infeas2 = norm(Aeq*solution - beq,Inf)

infeas2 = 
3.1378e-11

检查整数分量是否确实是整数，或者是否足够接近整数以便合理地对其进行四舍五入。要了解为什么这些变量可能不完全是整数，请参阅有些“整数”解不是整数。

diffint = norm(solution(intcon) - round(solution(intcon)),Inf)

diffint = 
6.7069e-14

有些整数变量并不完全是整数，但都非常接近整数。因此对整数变量进行四舍五入。

solution(intcon) = round(solution(intcon));

检查取整解的可行性，以及目标函数值的变化。

infeas1 = max(Aineq*solution - bineq)

infeas1 = 
8.4128e-12

infeas2 = norm(Aeq*solution - beq,Inf)

infeas2 = 
4.0302e-11

diffrounding = norm(fval - obj(:)'*solution,Inf)

diffrounding = 
1.8626e-08

对解进行四舍五入并没有明显改变其可行性。

您可以通过将其重新调整回其原始尺寸来最轻松地检查解。

solution1 = solution(1:P*F*W); % The continuous variables
solution2 = solution(intcon); % The integer variables
solution1 = reshape(solution1,P,F,W);
solution2 = reshape(solution2,S,W);

例如，每个仓库关联多少个销售网点？请注意，在这种情况下，一些仓库有 0 个关联出口，这意味着这些仓库在最佳解中未被使用。

outlets = sum(solution2,1) % Sum over the sales outlets

outlets = 1×20

     2     0     3     2     2     3     3     2     3     2     0     0     0     3     4     3     2     3     2     1

绘制每个销售网点与其仓库之间的连接。

figure(h);
hold on
for ii = 1:S
    jj = find(solution2(ii,:)); % Index of warehouse associated with ii
    xsales = xloc(F+W+ii); ysales = yloc(F+W+ii);
    xwarehouse = xloc(F+jj); ywarehouse = yloc(F+jj);
    if rand(1) < .5 % Draw y direction first half the time
        plot([xsales,xsales,xwarehouse],[ysales,ywarehouse,ywarehouse],'g--')
    else % Draw x direction first the rest of the time
        plot([xsales,xwarehouse,xwarehouse],[ysales,ysales,ywarehouse],'g--')
    end
end
hold off

title('Mapping of sales outlets to warehouses')

Figure contains an axes object. The axes object with title Mapping of sales outlets to warehouses contains 43 objects of type line. One or more of the lines displays its values using only markers These objects represent Factory, Warehouse, Sales outlet.

没有绿线的黑色*代表未使用的仓库。

另请参阅

主题

工厂、仓库、销售分配模型：基于问题