lsqnonlin 与 Simulink 模型

此示例显示如何调整 Simulink® 模型的参数。运行此示例时，将包含模型 optsim。该模型包括一个以 Simulink 框图建模的非线性过程工厂。

执行器饱和的工厂

该设备是一个具有执行器限制的欠阻尼三阶模型。执行器的限制是饱和限制和斜率限制。执行器饱和限制会切断大于 2 个单位或小于 -2 个单位的输入值。执行器的斜率限制为 0.8 单位/秒。系统对阶跃输入的闭环响应如闭环响应所示。您可以通过打开模型（在命令行中输入 optsim 或点击模型名称）并从仿真菜单中选择运行来查看此响应。响应绘制在范围内。

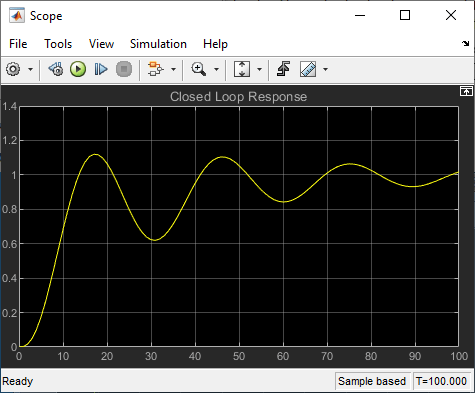
闭环响应

问题是设计一个反馈控制回路来跟踪系统的单位阶跃输入。闭环设备是按照设备和执行器位于分层 Subsystem 块中的块来输入的。Scope 块显示设计过程中的输出轨迹。

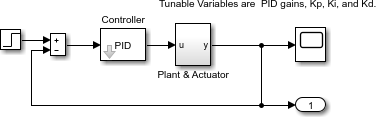
闭环模型

为了求解这个问题，尽量减少输出和输入信号之间的误差。（相反，在示例 将 fminimax 与 Simulink 模型结合使用 中，解涉及最小化输出的最大值。）这些变量是比例积分微分 (PID) 控制器的参数。如果您只需要最小化一个时间单位内的错误，那么您将有一个标量目标函数。但目标是最小化从 0 到 100 的所有时间步骤的误差，从而产生一个多目标函数（每个时间步骤一个函数）。

使用 lsqnonlin 对输出的跟踪执行最小二乘拟合。跟踪由函数 tracklsq 执行，该函数嵌套在本例末尾的 runtracklsq 中。tracklsq 返回误差信号 yout，即通过调用 sim 计算出的输出减去输入信号 1。

函数 runtracklsq 设置所有必需的值，然后使用目标函数 lsqnonlin 调用 tracklsq。传递给 options 的变量 lsqnonlin 定义了标准和显示特征。选项指定不显示输出，使用 'levenberg-marquardt' 算法，并且选项为步骤和目标函数提供大约 0.001 的终止公差。

为了在模型 optsim 中运行模拟，必须指定变量 Kp、Ki、Kd、a1 和 a2（a1 和 a2 是 Plant 块中的变量）。Kp、Ki 和 Kd 是需要优化的变量。函数 tracklsq 嵌套在 runtracklsq 内部，这样变量 a1 和 a2 在两个函数之间共享。变量 a1 和 a2 在 runtracklsq 中初始化。

目标函数 tracklsq 运行模拟。您可以在基础工作区或当前工作区中运行模拟，即调用 sim 的函数的工作区，在本例中是 tracklsq 的工作区。在这个示例中，SrcWorkspace 选项设置为 'Current'，以告诉 sim 在当前工作区中运行模拟。runtracklsq 将模拟运行至 100 秒。

当模拟完成后，runtracklsq 会在当前工作区（即 myobj 的工作区）中创建 tracklsq 对象。框图模型中的 Outport 块在模拟结束时将对象的 yout 字段放入当前工作区。

当您运行 runtracklsq 时，优化会为控制器的比例、积分和微分（Kp、Ki、Kd）增益提供解。示波器显示了优化的闭环阶跃响应。

[Kp, Ki, Kd] = runtracklsq

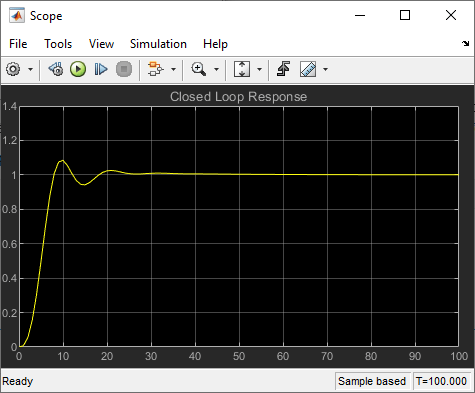
Kp = 
3.1330

Ki = 
0.1465

Kd = 
14.3918

注意：对 sim 的调用会导致对 Simulink 常微分方程 (ODE) 求解器之一的调用。您需要选择使用哪种类型的求解器。从优化的角度来看，如果足以求解 ODE，则固定步长 ODE 求解器是最佳选择。然而，在刚性系统的情况下，可能需要采用变步长 ODE 方法来求解 ODE。

然而，由于步长控制机制，变步长求解器产生的数值解并不是参数的平滑函数。这种缺乏平滑性的情况会阻止优化程序收敛。当您使用固定步长求解器时，缺乏平滑度就不是问题了。（有关进一步解释，请参阅 [53]。）

建议使用 Simulink Design Optimization™ 软件与 Simulink 可变步长求解器结合来求解多目标优化问题。该软件提供了一种特殊的数字梯度计算，可与 Simulink 配合使用，并避免引入缺乏平滑度的问题。

function [Kp,Ki,Kd] = runtracklsq
% RUNTRACKLSQ demonstrates using LSQNONLIN with Simulink.
mdl = 'optsim';
open_system(mdl)                             % Load the model
in = Simulink.SimulationInput(mdl);          % Create simulation input object
in = in.setModelParameter('StopTime','100'); % Stop time 100
pid0 = [0.63 0.0504 1.9688];                 % Initial gain values
a1 = 3; a2 = 43;                             % Initialize model plant variables
options = optimoptions(@lsqnonlin,'Algorithm','levenberg-marquardt',...
   'Display','off','StepTolerance',0.001,'OptimalityTolerance',0.001);
% Optimize the gains
set_param(mdl,'FastRestart','on');           % Fast restart
pid = lsqnonlin(@tracklsq,pid0,[],[],options);
set_param(mdl,'FastRestart','off');
% Return the gains
Kp = pid(1); Ki = pid(2); Kd = pid(3); 

    function F = tracklsq(pid)
      % Track the output of optsim to a signal of 1
      % Set the simulation input object parameters
      in = in.setVariable('Kp',pid(1),'Workspace',mdl);
      in = in.setVariable('Ki',pid(2),'Workspace',mdl);
      in = in.setVariable('Kd',pid(3),'Workspace',mdl);
      
      % Simulate
      out = sim(in);
      F = out.get('yout') - 1;
    end
end