使用线性规划实现长期投资最大化：基于问题

打开实时脚本

此示例说明如何使用基于问题的方法来求解固定年数内具有确定性回报的投资问题 T。问题在于如何将您的资金分配到可用的投资中，以最大化您的最终财富。有关基于求解器的方法，请参阅使用线性规划实现长期投资最大化：基于求解器。

问题表示

假设您有初始金额 Capital_0，准备在 T 年期限内投资 N 零息债券。每张债券支付固定利率，每年复利投资，并在到期时支付本金和复利。目标是最大化 T 年后返还的总金额。

您可以添加一个约束，即投资时任何单项投资不得超过您总资本的一定比例。

这个示例首先展示了小案例的问题设置，然后构造了一般情况。

您可以将其建模为线性规划问题。因此，为了优化您的财富，请使用优化问题方法来构造问题。

介绍性示例

从一个小示例开始：

Capital_0 的投资起始金额为 1000 美元。
时间段 T 为 5 年。
N 债券的数量为 4。
为了对未投资资金建模，每年提供一个选项 B0，其到期期限为 1 年，利率为 0%。
债券 1，标记为 B1，可在第 1 年购买，期限为 4 年，利率为 2%。
债券 2，标记为 B2，可在第 5 年购买，期限为 1 年，利率为 4%。
债券 3，标记为 B3，可在第 2 年购买，期限为 4 年，利率为 6%。
债券 4，标记为 B4，可在第 2 年购买，期限为 3 年，利率为 6%。

通过将第一个期权 B0 拆分为 5 张债券，期限为 1 年，利率为 0%，该问题可以等效建模为总共有 9 张可用债券，因此对于 k=1..9

向量 k 的条目 PurchaseYears 代表债券 k 可以购买的年份的年初。
向量 k 的条目 Maturity 代表债券 k 的到期期限 $m_{k}$ 。
向量 k 的条目 MaturityYears 代表债券 k 可供出售的年份年底。
向量 k 的条目 InterestRates 代表债券 k 的百分比利率 $ρ_{k}$ 。

通过代表每张债券可用购买时间和期限的水平条来直观地展示这个问题。

% Time period in years
T = 5;
% Number of bonds
N = 4;
% Initial amount of money
Capital_0 = 1000;
% Total number of buying opportunities
nPtotal = N+T;
% Purchase times
PurchaseYears = [1;2;3;4;5;1;5;2;2];
% Bond durations
Maturity = [1;1;1;1;1;4;1;4;3];
% Bond sale times
MaturityYears = PurchaseYears + Maturity - 1;
% Interest rates in percent
InterestRates = [0;0;0;0;0;2;4;6;6];
% Return after one year of interest
rt = 1 + InterestRates/100;

plotInvestments(N,PurchaseYears,Maturity,InterestRates)

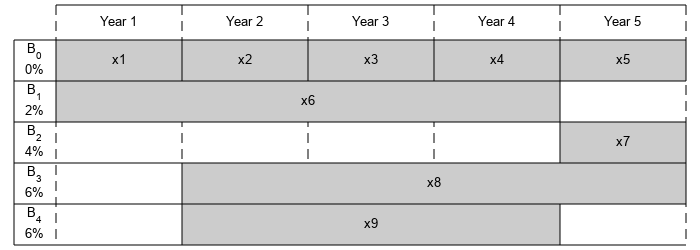
Figure contains an axes object. The hidden axes object contains 4 objects of type line.

决策变量

用向量 x 表示您的决策变量，其中 x(k) 是债券 k 的投资美元金额，对于 k = 1,...,9。到期后，投资 x(k) 的收益为

$x (k) (1 + ρ_{k} / 100)^{m_{k}} .$

定义 $β_{k} = 1 + ρ_{k} / 100$ 并将 $r_{k}$ 定义为债券 k 的总回报：

$r_{k} = (1 + ρ_{k} / 100)^{m_{k}} = β_{k}^{m_{k}} .$

x = optimvar('x',nPtotal,'LowerBound',0);
% Total returns
r = rt.^Maturity;

目标函数

目标是选择投资来最大化年末所收集的资金量 T。从图中可以看出，投资是在各个中间年份收集并再投资的。在第 T 年末，您可以收回投资 5、7 和 8 所返还的资金，这代表了您的最终财富：

$\max_{x} x_{5} r_{5} + x_{7} r_{7} + x_{8} r_{8}$

创建一个最大化的优化问题，并包含目标函数。

interestprob = optimproblem('ObjectiveSense','maximize');
interestprob.Objective = x(5)*r(5) + x(7)*r(7) + x(8)*r(8);

线性约束：不要投资超过您拥有的

每年，您都会有一定数量的资金可用于购买债券。从第 1 年开始，您可以将初始资本投资于购买期权 $x_{1}$ 和 $x_{6}$ ，因此：

$x_{1} + x_{6} = {C a p i t a l}_{0}$

然后在接下来的几年里，您收集到期债券的收益，并将其再投资于新的可用债券以获得方程组：

$\begin{array}{ll} x_{2} + x_{8} + x_{9} & = r_{1} x_{1} \\ x_{3} & = r_{2} x_{2} \\ x_{4} & = r_{3} x_{3} \\ x_{5} + x_{7} & = r_{4} x_{4} + r_{6} x_{6} + r_{9} x_{9} \end{array}$

investconstr = optimconstr(T,1);
investconstr(1) = x(1) + x(6) == Capital_0;
investconstr(2) = x(2) + x(8) + x(9) == r(1)*x(1);
investconstr(3) = x(3) == r(2)*x(2);
investconstr(4) = x(4) == r(3)*x(3);
investconstr(5) = x(5) + x(7) == r(4)*x(4) + r(6)*x(6) + r(9)*x(9);
interestprob.Constraints.investconstr = investconstr;

边界约束：禁止借贷

因为每个投资金额必须为正，所以解向量 $x$ 中的每个条目都必须为正。通过设置解向量 $x$ 的下界来包含此约束。解向量没有明确的上界。

x.LowerBound = 0;

求解问题

求解这个问题时，对您可以投资债券的金额没有任何约束。内点算法可以用来求解此类线性规划问题。

options = optimoptions('linprog','Algorithm','interior-point');
[sol,fval,exitflag] = solve(interestprob,'options',options)

Solving problem using linprog.

Solution found during presolve.

sol = struct with fields:
    x: [9×1 double]

fval = 
1.2625e+03

exitflag = 
    OptimalSolution

可视化解

退出标志表明求解器找到了最佳解。作为第二个输出参量返回的值 fval 对应于最终财富。查看最终的投资总额，以及随时间推移的投资分配。

fprintf('After %d years, the return for the initial $%g is $%g \n',...
    T,Capital_0,fval);

After 5 years, the return for the initial $1000 is $1262.48

plotInvestments(N,PurchaseYears,Maturity,InterestRates,sol.x)

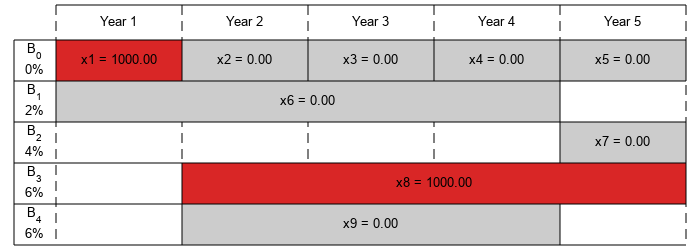
Figure contains an axes object. The hidden axes object contains 4 objects of type line.

有限持股的最优投资

为了分散您的投资，您可以选择将投资于任何一只债券的金额限制为当年总资本的一定百分比 Pmax（包括目前处于到期期的债券的回报）。您将获得以下不等式系统：

$\begin{array}{ll} x_{1} & \leq P m a x \times {C a p i t a l}_{0} \\ x_{2} & \leq P m a x \times (β_{1} x_{1} + β_{6} x_{6}) \\ x_{3} & \leq P m a x \times (β_{2} x_{2} + β_{6}^{2} x_{6} + β_{8} x_{8} + β_{9} x_{9}) \\ x_{4} & \leq P m a x \times (β_{3} x_{3} + β_{6}^{3} x_{6} + β_{8}^{2} x_{8} + β_{9}^{2} x_{9}) \\ x_{5} & \leq P m a x \times (β_{4} x_{4} + β_{6}^{4} x_{4} + β_{8}^{3} x_{8} + β_{9}^{3} x_{9}) \\ x_{6} & \leq P m a x \times {C a p i t a l}_{0} \\ x_{7} & \leq P m a x \times (β_{4} x_{4} + β_{6}^{4} x_{4} + β_{8}^{3} x_{8} + β_{9}^{3} x_{9}) \\ x_{8} & \leq P m a x \times (β_{1} x_{1} + β_{6} x_{6}) \\ x_{9} & \leq P m a x \times (β_{1} x_{1} + β_{6} x_{6}) \end{array}$

% Maximum percentage to invest in any bond
Pmax = 0.6;

constrlimit = optimconstr(nPtotal,1);
constrlimit(1) = x(1) <= Pmax*Capital_0;
constrlimit(2) = x(2) <= Pmax*(rt(1)*x(1) + rt(6)*x(6));
constrlimit(3) = x(3) <= Pmax*(rt(2)*x(2) + rt(6)^2*x(6) + rt(8)*x(8) + rt(9)*x(9));
constrlimit(4) = x(4) <= Pmax*(rt(3)*x(3) + rt(6)^3*x(6) + rt(8)^2*x(8) + rt(9)^2*x(9));
constrlimit(5) = x(5) <= Pmax*(rt(4)*x(4) + rt(6)^4*x(6) + rt(8)^3*x(8) + rt(9)^3*x(9));
constrlimit(6) = x(6) <= Pmax*Capital_0;
constrlimit(7) = x(7) <= Pmax*(rt(4)*x(4) + rt(6)^4*x(6) + rt(8)^3*x(8) + rt(9)^3*x(9));
constrlimit(8) = x(8) <= Pmax*(rt(1)*x(1) + rt(6)*x(6));
constrlimit(9) = x(9) <= Pmax*(rt(1)*x(1) + rt(6)*x(6));

interestprob.Constraints.constrlimit = constrlimit;

通过对任何一项资产的投资不超过 60% 来求解问题。绘制购买结果图。请注意，您的最终财富将少于没有此约束的投资。

[sol,fval] = solve(interestprob,'options',options);

Solving problem using linprog.

Minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in feasible directions, to within the function tolerance, and constraints are satisfied to within the constraint tolerance.

fprintf('After %d years, the return for the initial $%g is $%g \n',...
    T,Capital_0,fval);

After 5 years, the return for the initial $1000 is $1207.78

plotInvestments(N,PurchaseYears,Maturity,InterestRates,sol.x)

Figure contains an axes object. The hidden axes object contains 4 objects of type line.

任意尺寸模型

为该问题的一般版本创建一个模型。使用 T = 30 年和 400 个随机生成的债券（利率从 1% 到 6%）来说明。此设置产生一个具有 430 个决策变量的线性规划问题。

% For reproducibility
rng default 
% Initial amount of money
Capital_0 = 1000;
% Time period in years
T = 30;
% Number of bonds
N = 400;
% Total number of buying opportunities
nPtotal = N + T;
% Generate random maturity durations
Maturity = randi([1 T-1],nPtotal,1);
% Bond 1 has a maturity period of 1 year
Maturity(1:T) = 1;
% Generate random yearly interest rate for each bond
InterestRates = randi(6,nPtotal,1);
% Bond 1 has an interest rate of 0 (not invested)
InterestRates(1:T) = 0;
% Return after one year of interest
rt = 1 + InterestRates/100;
% Compute the return at the end of the maturity period for each bond:
r = rt.^Maturity;

% Generate random purchase years for each option
PurchaseYears = zeros(nPtotal,1);
% Bond 1 is available for purchase every year
PurchaseYears(1:T)=1:T;
for i=1:N
    % Generate a random year for the bond to mature before the end of
    % the T year period
    PurchaseYears(i+T) = randi([1 T-Maturity(i+T)+1]);
end

% Compute the years where each bond reaches maturity at the end of the year
MaturityYears = PurchaseYears + Maturity - 1;

计算债券可以买入或卖出的时间。buyindex 矩阵保存每个债券的潜在购买时间，而 sellindex 矩阵保存每个债券的潜在销售时间。

buyindex = false(nPtotal,T); % allocate nPtotal-by-T matrix
for ii = 1:T
    buyindex(:,ii) = PurchaseYears == ii;
end
sellindex = false(nPtotal,T);
for ii = 1:T
    sellindex(:,ii) = MaturityYears == ii;
end

设置与债券相对应的优化变量。

x = optimvar('x',nPtotal,1,'LowerBound',0);

创建优化问题和目标函数。

interestprob = optimproblem('ObjectiveSense','maximize');
interestprob.Objective = sum(x(sellindex(:,T)).*r(sellindex(:,T)));

为了方便起见，创建一个临时数组 xBuy，其列代表我们在每个时间段可以购买的债券。

xBuy = repmat(x,1,T).*double(buyindex);

类似地，创建一个临时数组 xSell，其列代表我们可以在每个时间段内出售的债券。

xSell = repmat(x,1,T).*double(sellindex);

卖出这些债券产生的回报是

xReturnFromSell = xSell.*repmat(r,1,T);

创建约束，即您在每个时间段内投资的金额是您在上一时间段内销售的金额。

interestprob.Constraints.InitialInvest = sum(xBuy(:,1)) == Capital_0;
interestprob.Constraints.InvestConstraint = sum(xBuy(:,2:T),1) == sum(xReturnFromSell(:,1:T-1),1);

无限持股解

求解。

tic
[sol,fval,exitflag] = solve(interestprob,'options',options);

Solving problem using linprog.

Solution found during presolve.

toc

Elapsed time is 0.406917 seconds.

投资效果如何？

fprintf('After %d years, the return for the initial $%g is $%g \n',...
    T,Capital_0,fval);

After 30 years, the return for the initial $1000 is $5167.58

有限持股解

为了创建限制每项资产投资比例的约束，需要建立一个矩阵来跟踪每个时间的活跃债券。为了表达每项投资必须小于总价值 Pmax 倍的约束，请建立一个矩阵来跟踪每个时间的每项投资的价值。对于这个较大的问题，将可以保留的最大分数设置为 0.4。

Pmax = 0.4;

创建一个 active 矩阵，对应债券可持有的时间，以及一个 cactive 矩阵，保存每个活跃债券的累积持续时间。因此，债券 j 在时间 t 的价值为 x(j)*(rt^cactive)。

active = double(buyindex | sellindex);
for ii = 1:T
    active(:,ii) = double((ii >= PurchaseYears) & (ii <= MaturityYears));
end
cactive = cumsum(active,2);
cactive = cactive.*active;

创建矩阵，其条目 (j,p) 表示债券 j 在时间段 p 的价值：

bondValue = repmat(x, 1, T).*active.*(rt.^(cactive));

确定每个时间间隔内投资的总价值，以便可以对有限持有量施加约束。mvalue 是每个时间段结束时投资于所有债券的资金，一个 nPtotal×T 矩阵。moneyavailable 是时间段开始时投资于债券的资金总和，即每个时间的投资组合的价值。

constrlimit = optimconstr(nPtotal,T);
constrlimit(:,1) = xBuy(:,1) <= Pmax*Capital_0;
constrlimit(:,2:T) = xBuy(:,2:T)  <= repmat(Pmax*sum(bondValue(:,1:T-1),1), nPtotal, 1).*double(buyindex(:,2:T));
interestprob.Constraints.constrlimit = constrlimit;

求解持股受限的问题。

tic
[sol,fval,exitflag] = solve(interestprob,'options',options);

Solving problem using linprog.

Minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in feasible directions, to within the function tolerance, and constraints are satisfied to within the constraint tolerance.

toc

Elapsed time is 1.822707 seconds.

fprintf('After %d years, the return for the initial $%g is $%g \n',...
    T,Capital_0,fval);

After 30 years, the return for the initial $1000 is $5095.26

为了加快求解器的速度，请尝试对偶单纯形算法。

options = optimoptions('linprog','Algorithm','dual-simplex');
tic
[sol,fval,exitflag] = solve(interestprob,'options',options);

Solving problem using linprog.

Optimal solution found.

toc

Elapsed time is 0.254835 seconds.

fprintf('After %d years, the return for the initial $%g is $%g \n',...
    T,Capital_0,fval);

After 30 years, the return for the initial $1000 is $5095.26

在这种情况下，对偶单纯形算法花费更少的时间来获得相同的解。

定性结果分析

为了对解有个大概的了解，请将其与如果您可以在整个 30 年期间将所有启动资金投资于一张利率为 6%（最高利率）的债券，您将获得的金额 fmax 进行比较。您还可以计算与您的最终财富相对应的等值利率。

% Maximum amount
fmax = Capital_0*(1+6/100)^T;
% Ratio (in percent)
rat = fval/fmax*100;
% Equivalent interest rate (in percent)
rsol = ((fval/Capital_0)^(1/T)-1)*100;

fprintf(['The amount collected is %g%% of the maximum amount $%g '...
    'that you would obtain from investing in one bond.\n'...
    'Your final wealth corresponds to a %g%% interest rate over the %d year '...
    'period.\n'], rat, fmax, rsol, T)

The amount collected is 88.7137% of the maximum amount $5743.49 that you would obtain from investing in one bond.
Your final wealth corresponds to a 5.57771% interest rate over the 30 year period.

plotInvestments(N,PurchaseYears,Maturity,InterestRates,sol.x,false)

Figure contains an axes object. The hidden axes object contains 2 objects of type line.

使用线性规划实现长期投资最大化：基于问题

问题表示

介绍性示例

决策变量

目标函数

线性约束：不要投资超过您拥有的

边界约束：禁止借贷

求解问题

可视化解

有限持股的最优投资

任意尺寸模型

无限持股解

有限持股解

定性结果分析

另请参阅

主题