在基于问题的框架中创建多周期库存模型
此示例展示如何在基于问题的框架中创建多周期库存模型。问题在于在一段时间内安排使用多种成分的肥料混合物的生产,这些成分的成本以可预测的方式依赖于时间。假设您事先知道肥料的需求量。目标是在满足需求的同时实现利润最大化,其成本是购买原材料和长期储存肥料。您可以使用期货或其他合约提前确定成本。
肥料和成分
颗粒肥料含有氮 (N)、磷 (P) 和钾 (K) 等营养成分。您可以混合以下原材料以获得含有所需营养成分的肥料混合物。
load fertilizer blends = blendDemand.Properties.VariableNames % Fertilizers to produce
blends = 1×2 cell
{'Balanced'} {'HighN'}
nutrients = rawNutrients.Properties.RowNames
nutrients = 3×1 cell
{'N'}
{'P'}
{'K'}
raws = rawNutrients.Properties.VariableNames % Raw materialsraws = 1×6 cell
{'MAP'} {'Potash'} {'AN'} {'AS'} {'TSP'} {'Sand'}
两种肥料混合物具有相同的营养需求(按重量计 10% N、10% P 和 10% K),但“HighN”混合物额外含有 10% N,总计 20% N。
disp(blendNutrients) % Table is in percentage Balanced HighN
________ _____
N 10 20
P 10 10
K 10 10
原料的名称和营养成分(按重量计)百分比如下。
disp(rawNutrients) % Table is in percentage MAP Potash AN AS TSP Sand
___ ______ __ __ ___ ____
N 11 0 35 21 0 0
P 48 0 0 0 46 0
K 0 60 0 0 0 0
原料 Sand 没有任何营养成分。如果有必要,沙子会稀释其他成分,以获得所需重量百分比的营养成分。
将每个数量的数量存储在变量中。
nBlends = length(blends); nRaws = length(raws); nNutrients = length(nutrients);
预测需求和收入
假设您事先知道问题时间段内两种肥料混合物的需求重量(吨)。
disp(blendDemand)
Balanced HighN
________ _____
January 750 300
February 800 310
March 900 600
April 850 400
May 700 350
June 700 300
July 700 200
August 600 200
September 600 200
October 550 200
November 550 200
December 550 200
您知道每吨肥料混合物的销售价格。这些每吨价格与时间无关。
disp(blendPrice)
Balanced HighN
________ _____
400 550
原材料价格
假设您事先知道原材料的吨价。根据下表,每吨价格随时间而变化。
disp(rawCost)
MAP Potash AN AS TSP Sand
___ ______ ___ ___ ___ ____
January 350 610 300 135 250 80
February 360 630 300 140 275 80
March 350 630 300 135 275 80
April 350 610 300 125 250 80
May 320 600 300 125 250 80
June 320 600 300 125 250 80
July 320 600 300 125 250 80
August 320 600 300 125 240 80
September 320 600 300 125 240 80
October 310 600 300 125 240 80
November 310 600 300 125 240 80
December 340 600 300 125 240 80
储存成本
混合肥料的储存成本按每吨和每个时间段计算。
disp(inventoryCost)
10
容量约束
在任何时间段内,您最多可以储存 inventoryCapacity 吨的肥料混合物。
disp(inventoryCapacity)
1000
在任何时间段内,您总共可以生产不超过 productionCapacity 吨。
disp(productionCapacity)
1200
生产、销售和库存之间的联系
您首先要制定计划,计划中要有一定数量或库存的肥料混合物。您对这个库存在最后时期有一个确定的目标。在每个时间段,肥料混合物的数量等于上一个时间段结束时的数量加上生产的数量减去销售的数量。换句话说,对于大于 1 的次数:
inventory(time,product) = inventory(time-1,product) + production(time,product) - sales(time,product)
这个等式意味着库存是在时间段结束时进行盘点的。问题中的时间段如下。
months = blendDemand.Properties.RowNames; nMonths = length(months);
初始库存对时间 1 时的库存有如下影响。
inventory(1,product) = initialInventory(product) + production(1,product) - sales(1,product)
初始库存在数据 blendInventory{'Initial',:} 中。最终库存在数据 blendInventory{'Final',:} 中。
假设未满足的需求丢失了。换句话说,如果您无法在某个时间段内完成所有订单,那么多余的订单将不会结转到下一个时间段。
优化问题表示
该问题的目标函数是利润,您希望将其最大化。因此,在基于问题的框架中创建一个最大化问题。
inventoryProblem = optimproblem('ObjectiveSense','maximize');
该问题的变量是您每月生产和销售的肥料混合物的数量,以及用于制造这些混合物的原材料。sell 的上界是每个时间段和每种肥料混合物的需求,blendDemand。
make = optimvar('make',months,blends,'LowerBound',0); sell = optimvar('sell',months,blends,'LowerBound',0,'UpperBound',blendDemand{months,blends}); use = optimvar('use',months,raws,blends,'LowerBound',0);
此外,创建一个代表每次库存的变量。
inventory = optimvar('inventory',months,blends,'LowerBound',0,'UpperBound',inventoryCapacity);
根据问题变量计算目标函数,计算收入和成本。收入等于每种肥料混合物的销量乘以价格,再加上所有时间段和混合物。
revenue = sum(blendPrice{1,:}.*sum(sell(months,blends),1));原料成本是每次使用的每种原料的成本在所有时间段内相加。因为每次使用的量都分成了每种混合物使用的量,所以也要添加混合物。
blendsUsed = sum(use(months,raws,blends),3);
ingredientCost = sum(sum(rawCost{months,raws}.*blendsUsed));仓储成本是每个时间段内仓储库存的成本,是随着时间的推移而增加和混合而成的。
storageCost = inventoryCost*sum(inventory(:));
现在使用点符号将目标函数放入问题的 Objective 属性中。
inventoryProblem.Objective = revenue - ingredientCost - storageCost;
问题约束
这个问题有几个约束。首先,将库存方程表示为问题变量的一组约束。
materialBalance = optimconstr(months,blends); timeAbove1 = months(2:end); previousTime = months(1:end-1); materialBalance(timeAbove1,:) = inventory(timeAbove1,:) == inventory(previousTime,:) +... make(timeAbove1,:) - sell(timeAbove1,:); materialBalance(1,:) = inventory(1,:) == blendInventory{'Initial',:} +... make(1,:) - sell(1,:);
表达最终库存也是固定的约束。
finalC = inventory(end,:) == blendInventory{'Final',:};每个时刻的总库存都是有限的。
boundedInv = sum(inventory,2) <= inventoryCapacity;
每个时间段内您可以生产有限的数量。
processLimit = sum(make,2) <= productionCapacity;
您每月生产的每种混合物的量就是您使用的原材料的量。squeeze 函数将总和从 nmonths×1×nblends 数组转换为 nmonths×nblends 数组。
rawMaterialUse = squeeze(sum(use(months,raws,blends),2)) == make(months,blends);
每种混合物中的营养成分必须具有必要的值。在下面的内部语句中,乘法 rawNutrients{n,raws}*use(m,raws,b)' 将每次的营养值添加到所用的原材料上。
blendNutrientsQuality = optimconstr(months,nutrients,blends); for m = 1:nMonths for b = 1:nBlends for n = 1:nNutrients blendNutrientsQuality(m,n,b) = rawNutrients{n,raws}*use(m,raws,b)' == blendNutrients{n,b}*make(m,b); end end end
将约束放入问题中。
inventoryProblem.Constraints.materialBalance = materialBalance; inventoryProblem.Constraints.finalC = finalC; inventoryProblem.Constraints.boundedInv = boundedInv; inventoryProblem.Constraints.processLimit = processLimit; inventoryProblem.Constraints.rawMaterialUse = rawMaterialUse; inventoryProblem.Constraints.blendNutrientsQuality = blendNutrientsQuality;
求解问题
问题表示已完成。求解。
[sol,fval,exitflag,output] = solve(inventoryProblem)
Solving problem using linprog. Optimal solution found.
sol = struct with fields:
inventory: [12×2 double]
make: [12×2 double]
sell: [12×2 double]
use: [12×6×2 double]
fval = 2.2474e+06
exitflag =
OptimalSolution
output = struct with fields:
iterations: 110
algorithm: 'dual-simplex-highs'
constrviolation: 9.0949e-13
message: 'Optimal solution found.'
firstorderopt: 1.1369e-13
solver: 'linprog'
以表格和图形形式显示结果。
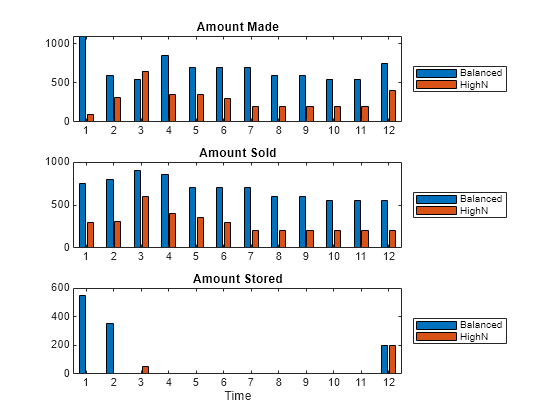
if exitflag > 0 fprintf('Profit: %g\n',fval); makeT = array2table(sol.make,'RowNames',months,'VariableNames',strcat('make',blends)); sellT = array2table(sol.sell,'RowNames',months,'VariableNames',strcat('sell',blends)); storeT = array2table(sol.inventory,'RowNames',months,'VariableNames',strcat('store',blends)); productionPlanT = [makeT sellT storeT] figure subplot(3,1,1) bar(sol.make) legend('Balanced','HighN','Location','eastoutside') title('Amount Made') subplot(3,1,2) bar(sol.sell) legend('Balanced','HighN','Location','eastoutside') title('Amount Sold') subplot(3,1,3) bar(sol.inventory) legend('Balanced','HighN','Location','eastoutside') title('Amount Stored') xlabel('Time') end
Profit: 2.24739e+06
productionPlanT=12×6 table
makeBalanced makeHighN sellBalanced sellHighN storeBalanced storeHighN
____________ _________ ____________ _________ _____________ __________
January 1100 100 750 300 550 0
February 600 310 800 310 350 0
March 550 650 900 600 0 50
April 850 350 850 400 0 0
May 700 350 700 350 0 0
June 700 300 700 300 0 0
July 700 200 700 200 0 0
August 600 200 600 200 0 0
September 600 200 600 200 0 0
October 550 200 550 200 0 0
November 550 200 550 200 0 0
December 750 400 550 200 200 200