通过二元整数规划进行办公室分配:基于问题
此示例说明如何使用优化问题方法通过二元整数规划解决分配问题。有关基于求解器的方法,请参阅通过二元整数规划进行办公室分配:基于求解器。
办公室分配问题
您想要将 Marcelo、Rakesh、Peter、Tom、Marjorie 和 Mary Ann 六个人分配到七间办公室。每间办公室最多只能有一个人,并且每个人只能有一间办公室。因此将会有一间空办公室。人们可以提出自己对办公室的偏好,分配时会结合每个人的资历来考虑他们的偏好。他们在 MathWorks 工作的时间越长,资历就越高。有些办公室有窗户,有些没有,而且有一扇窗户比其他的窗户小。此外,Peter 和 Tom 经常一起工作,因此应该在相邻的办公室。Marcelo 和 Rakesh 经常一起工作,应该在相邻的办公室。
办公室布局
办公室 1、2、3 和 4 属于内区办公室(没有窗户)。5、6 和 7 号办公室都有窗户,但 5 号办公室的窗户比其他两个办公室的窗户小。办公室的布置如下。
officelist = {'Office 1','Office 2','Office 3','Office 4','Office 5','Office 6','Office 7'};
printofficeassign(officelist)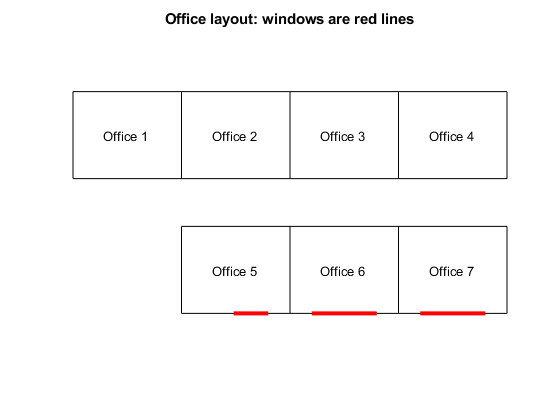
问题表示
您需要用数学方法表示这个问题。创建二元变量来指示一个人是否占用办公室。人员名单如下
namelist = {'Mary Ann','Marjorie','Tom','Peter','Marcelo','Rakesh'};创建按办公室编号和名称索引的二元变量。
occupy = optimvar('occupy',namelist,officelist,... 'Type','integer','LowerBound',0,'Upperbound',1);
资历
您希望根据资历对偏好进行加权。这样,在 MathWorks 工作的时间越长,偏好的权重就越高。资历如下:Mary Ann 9 年、Marjorie 10 年、Tom 5 年、Peter 3 年、Marcelo 1.5 年、Rakesh 2 年。根据资历创建一个归一化的权重向量。
seniority = [9 10 5 3 1.5 2]; weightvector = seniority/sum(seniority);
人们的办公室偏好
设置一个偏好矩阵,其中行对应于办公室,列对应于人。要求每个人为每间办公室给出一个数值,使得他们所有选择(即他们的各个列)的总和等于 100。数字越大表示此人更喜欢该办公室。每个人的偏好都列在一个列向量中。
MaryAnn = [0, 0, 0, 0, 10, 40, 50]; Marjorie = [0, 0, 0, 0, 20, 40, 40]; Tom = [0, 0, 0, 0, 30, 40, 30]; Peter = [1, 3, 3, 3, 10, 40, 40]; Marcelo = [3, 4, 1, 2, 10, 40, 40]; Rakesh = [10, 10, 10, 10, 20, 20, 20];
一个人的偏好向量的第 i 个元素表示他们对第 i 个办公室的偏好程度。因此,合并后的偏好矩阵如下:
prefmatrix = [MaryAnn;Marjorie;Tom;Peter;Marcelo;Rakesh];
通过 weightvector 对偏好矩阵进行加权,以按资历缩放列。
PM = diag(weightvector) * prefmatrix;
目标函数
目标是最大限度地满足按资历加权的偏好。这是线性目标函数 sum(sum(occupy.*PM))。
创建一个优化问题并加入目标函数。
peopleprob = optimproblem('ObjectiveSense','maximize','Objective',sum(sum(occupy.*PM)));
约束
第一组约束要求每个人恰好分得一间办公室,也就是说,对于每个人来说,与其对应的 occupy 值的总和恰好为 1。
peopleprob.Constraints.constr1 = sum(occupy,2) == 1;
第二组约束是不等式。这些约束规定每个办公室最多只能有一个人。
peopleprob.Constraints.constr2 = sum(occupy,1) <= 1;
您希望 Tom 和 Peter 之间的办公室距离不超过一个办公室,Marcelo 和 Rakesh 之间的办公室距离也同样如此。
设定约束:Tom 和 Peter 之间的距离不超过 1。
peopleprob.Constraints.constrpt1 = occupy('Tom','Office 1') + sum(occupy('Peter',:)) - occupy('Peter','Office 2') <= 1; peopleprob.Constraints.constrpt2 = occupy('Tom','Office 2') + sum(occupy('Peter',:)) - occupy('Peter','Office 1') ... - occupy('Peter','Office 3') - occupy('Peter','Office 5') <= 1; peopleprob.Constraints.constrpt3 = occupy('Tom','Office 3') + sum(occupy('Peter',:)) - occupy('Peter','Office 2') ... - occupy('Peter','Office 4') - occupy('Peter','Office 6') <= 1; peopleprob.Constraints.constrpt4 = occupy('Tom','Office 4') + sum(occupy('Peter',:)) - occupy('Peter','Office 3') ... - occupy('Peter','Office 7') <= 1; peopleprob.Constraints.constrpt5 = occupy('Tom','Office 5') + sum(occupy('Peter',:)) - occupy('Peter','Office 2') ... - occupy('Peter','Office 6') <= 1; peopleprob.Constraints.constrpt6 = occupy('Tom','Office 6') + sum(occupy('Peter',:)) - occupy('Peter','Office 3') ... - occupy('Peter','Office 5') - occupy('Peter','Office 7') <= 1; peopleprob.Constraints.constrpt7 = occupy('Tom','Office 7') + sum(occupy('Peter',:)) - occupy('Peter','Office 4') ... - occupy('Peter','Office 6') <= 1;
现在创建约束,使得 Marcelo 和 Rakesh 之间的距离不超过 1。
peopleprob.Constraints.constmr1 = occupy('Marcelo','Office 1') + sum(occupy('Rakesh',:)) - occupy('Rakesh','Office 2') <= 1; peopleprob.Constraints.constmr2 = occupy('Marcelo','Office 2') + sum(occupy('Rakesh',:)) - occupy('Rakesh','Office 1') ... - occupy('Rakesh','Office 3') - occupy('Rakesh','Office 5') <= 1; peopleprob.Constraints.constmr3 = occupy('Marcelo','Office 3') + sum(occupy('Rakesh',:)) - occupy('Rakesh','Office 2') ... - occupy('Rakesh','Office 4') - occupy('Rakesh','Office 6') <= 1; peopleprob.Constraints.constmr4 = occupy('Marcelo','Office 4') + sum(occupy('Rakesh',:)) - occupy('Rakesh','Office 3') ... - occupy('Rakesh','Office 7') <= 1; peopleprob.Constraints.constmr5 = occupy('Marcelo','Office 5') + sum(occupy('Rakesh',:)) - occupy('Rakesh','Office 2') ... - occupy('Rakesh','Office 6') <= 1; peopleprob.Constraints.constmr6 = occupy('Marcelo','Office 6') + sum(occupy('Rakesh',:)) - occupy('Rakesh','Office 3') ... - occupy('Rakesh','Office 5') - occupy('Rakesh','Office 7') <= 1; peopleprob.Constraints.constmr7 = occupy('Marcelo','Office 7') + sum(occupy('Rakesh',:)) - occupy('Rakesh','Office 4') ... - occupy('Rakesh','Office 6') <= 1;
求解分配问题
调用 solve 以求解问题。
[soln,fval,exitflag,output] = solve(peopleprob);
LP: Optimal objective value is -33.836066. Optimal solution found. Intlinprog stopped at the root node because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 0 (the default value). The intcon variables are integer within tolerance, options.IntegerTolerance = 1e-05 (the default value).
查看解 - 哪个人分得了哪间办公室?
numOffices = length(officelist); office = cell(numOffices,1); for i=1:numOffices office{i} = find(soln.occupy(:,i)); % people index in office end whoinoffice = officelist; % allocate for i=1:numOffices if isempty(office{i}) whoinoffice{i} = ' empty '; else whoinoffice{i} = namelist(office{i}); end end printofficeassign(whoinoffice); title('Solution of the Office Assignment Problem');
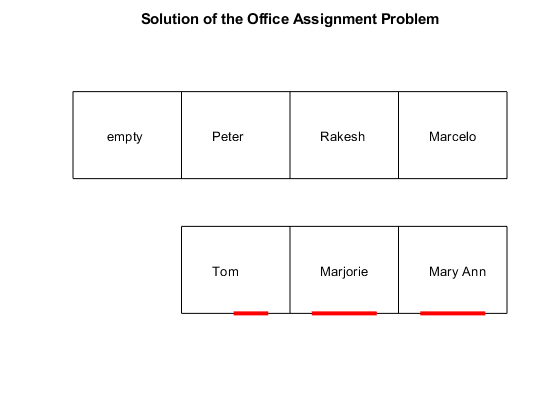
解质量
对于这个问题,通过最大化 fval 的值来满足按资历排序的偏好。exitflag 的值指示 solve 收敛到一个最优解。输出结构给出了求解过程的信息,例如探索了多少个节点,以及分支计算中下界和上界之间的差距。在这种情况下,没有生成分支定界节点,这意味着问题无需分支定界步骤即可解决。绝对差距为 0,表示解是最优的,内部计算的目标函数的下界和上界之间没有差异。
fval,exitflag,output
fval = 33.8361
exitflag = 1
output = struct with fields:
relativegap: 0
absolutegap: 0
numfeaspoints: 1
numnodes: 0
constrviolation: 0
message: 'Optimal solution found.↵↵Intlinprog stopped at the root node because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 0 (the default value). The intcon variables are integer within tolerance, options.IntegerTolerance = 1e-05 (the default value).'
solver: 'intlinprog'