通过二元整数规划进行办公室分配：基于求解器

办公室分配问题

您想要将 Marcelo、Rakesh、Peter、Tom、Marjorie 和 Mary Ann 六个人分配到七间办公室。每间办公室最多只能有一个人，并且每个人只能有一间办公室。因此将会有一间空办公室。人们可以提出自己对办公室的偏好，分配时会结合每个人的资历来考虑他们的偏好。他们在 MathWorks 工作的时间越长，资历就越高。有些办公室有窗户，有些没有，而且有一扇窗户比其他的窗户小。此外，Peter 和 Tom 经常一起工作，因此应该在相邻的办公室。Marcelo 和 Rakesh 经常一起工作，应该在相邻的办公室。

办公室布局

办公室 1、2、3 和 4 属于内区办公室（没有窗户）。5、6 和 7 号办公室都有窗户，但 5 号办公室的窗户比其他两个办公室的窗户小。办公室的布置如下。

name = {'Office 1','Office 2','Office 3','Office 4','Office 5','Office 6','Office 7'};
printofficeassign(name)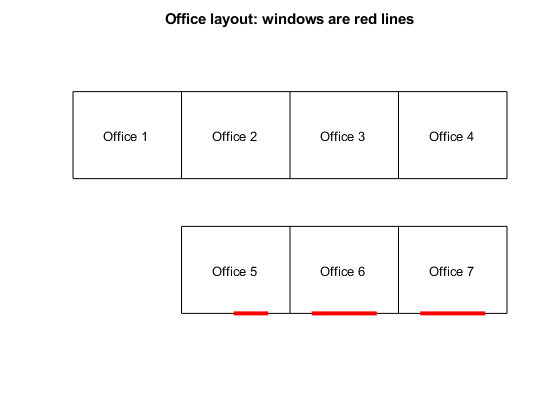

问题表示

您需要用数学方法表示这个问题。首先，选择解变量 x 的每个元素在问题中代表什么。由于这是一个二元整数问题，因此一个好的选择是每个元素代表一个人被分配至某一办公室。如果此人被分配至该办公室，则变量的值为 1。如果此人未分配至该办公室，则变量的值为 0。人员编号如下：

x 是一个向量。元素 x(1) 到 x(7) 对应于 Mary Ann 被分配至办公室 1、办公室 2，依此类推，直至办公室 7。接下来的七个元素对应于 Marjorie 被分配至七个办公室，依此类推。总共，x 向量有 42 个元素，因为六个人被分配至七间办公室。

资历

您希望根据资历对偏好进行加权。这样，在 MathWorks 工作的时间越长，偏好的权重就越高。资历如下：Mary Ann 9 年、Marjorie 10 年、Tom 5 年、Peter 3 年、Marcelo 1.5 年、Rakesh 2 年。根据资历创建一个归一化的权重向量。

seniority = [9 10 5 3 1.5 2];
weightvector = seniority/sum(seniority);

人们的办公室偏好

设置一个偏好矩阵，其中行对应于办公室，列对应于人。要求每个人为每间办公室给出一个数值，使得他们所有选择（即他们的各个列）的总和等于 100。数字越大表示此人更喜欢该办公室。每个人的偏好都列在一个列向量中。

MaryAnn = [0; 0; 0; 0; 10; 40; 50];
Marjorie = [0; 0; 0; 0; 20; 40; 40];
Tom = [0; 0; 0; 0; 30; 40; 30];
Peter = [1; 3; 3; 3; 10; 40; 40];
Marcelo = [3; 4; 1; 2; 10; 40; 40];
Rakesh = [10; 10; 10; 10; 20; 20; 20];

一个人的偏好向量的第 i 个元素表示他们对第 i 个办公室的偏好程度。因此，合并后的偏好矩阵如下：

prefmatrix = [MaryAnn Marjorie Tom Peter Marcelo Rakesh];

通过 weightvector 对偏好矩阵进行加权，以按资历缩放列。此外，将此矩阵重构为按列顺序排列的向量，以便与向量 x 对应。

PM = prefmatrix * diag(weightvector);
c = PM(:);

目标函数

目标是最大限度地满足按资历加权的偏好。这是一个线性目标函数

max c'*x

也可以是下面这个等价函数

min -c'*x.

约束

第一组约束要求每个人恰好分得一间办公室，也就是说，对于每个人来说，与其对应的 x 值的总和恰好为 1。例如，由于 Marjorie 是第二个人，这意味着 sum(x(8:14))=1 。通过构建适当的矩阵，在等式矩阵 Aeq 和向量beq（其中 Aeq*x = beq）中表示这些线性约束。矩阵 Aeq 由 1 和 0 组成。例如，Aeq 的第二行将对应于 Marjorie 分得一间办公室，因此该行如下所示：

0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 ... 0 0 0

第 8 列至第 14 列中有 7 个 1，其他列都为 0。那么 Aeq(2,:)*x = 1 等同于 sum(x(8:14)) = 1 。

numOffices = 7;
numPeople = 6;
numDim = numOffices * numPeople;
onesvector = ones(1,numOffices);

Aeq 的每一行对应一个人。

Aeq = blkdiag(onesvector,onesvector,onesvector,onesvector, ...
    onesvector,onesvector);
beq = ones(numPeople,1);

第二组约束是不等式。这些约束规定每间办公室中最多只能有一个人，即每个办公室只有一个人，或者为空。构建矩阵 A 和向量 b，使得 A*x <= b 能够捕获这些约束。A 和 b 的每一行对应一间办公室，因此第 1 行对应分配至办公室 1 的人员。这次，对于第 1 行，具有这种模式：

1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 ... 1 0 0 0 0 0 0

此后的每一行都类似，但（循环）向右移动一个位置。例如，第 3 行对应办公室 3，并表示 A(3,:)*x <= 1，即办公室 3 中不能容纳超过一个人。

A = repmat(eye(numOffices),1,numPeople);
b = ones(numOffices,1);

下一组约束也是不等式，因此将它们添加到已经包含上述不等式的矩阵 A 和向量 b 中。您希望 Tom 和 Peter 之间的办公室距离不超过一个办公室，Marcelo 和 Rakesh 之间的办公室距离也同样如此。首先，根据办公室的物理位置并使用近似的曼哈顿距离构建办公室的距离矩阵。这是一个对称矩阵。

D = zeros(numOffices);

设置矩阵的右上半部分。

D(1,2:end) = [1 2 3 2 3 4];
D(2,3:end) = [1 2 1 2 3];
D(3,4:end) = [1 2 1 2];
D(4,5:end) = [3 2 1];
D(5,6:end) = [1 2];
D(6,end)   = 1;

左下半部分与右上半部分相同。

D = triu(D)' + D;

查找距离超过一个距离单位的办公室。

[officeA,officeB] = find(D > 1);
numPairs = length(officeA)

numPairs = 26

这将找到 numPairs 对不相邻的办公室。对于这些配对，如果 Tom 占据配对中的一个办公室，那么 Peter 就不能占据配对中的另一间办公室。如果他这么做了，他们就不能相邻了。Marcelo 和 Rakesh 也是如此。这为 2*numPairs 提供了更多不等式约束，您可以将其添加到 A 和 b 中。

向 A 添加足够的行以适应这些约束。

numrows = 2*numPairs + numOffices; 
A((numOffices+1):numrows, 1:numDim) = zeros(2*numPairs,numDim);

对于 numPairs 中的每对办公室，与 officeA 中的 Tom 对应的 x(i) 以及与 OfficeB 中的 Peter 对应的 x(j)，满足

x(i) + x(j) <= 1.

这意味着 Tom 或 Peter 可以占据其中一间办公室，但他们不能同时占据。

Tom 是第 3 个人，Peter 是第 4 个人。

tom = 3;
peter = 4;

Marcelo 是第 5 个人，Rakesh 是第 6 个人。

marcelo = 5;
rakesh = 6;

以下匿名函数返回分别对应于 Tom、Peter、Marcelo 和 Rakesh 在办公室 i 中分配情况的 x 的索引。

tom_index=@(officenum) (tom-1)*numOffices+officenum;
peter_index=@(officenum) (peter-1)*numOffices+officenum;
marcelo_index=@(officenum) (marcelo-1)*numOffices+officenum;
rakesh_index=@(officenum) (rakesh-1)*numOffices+officenum;

for i = 1:numPairs    
    tomInOfficeA = tom_index(officeA(i));
    peterInOfficeB = peter_index(officeB(i));
    A(i+numOffices, [tomInOfficeA, peterInOfficeB]) = 1;
   
    % Repeat for Marcelo and Rakesh, adding more rows to A and b.
    marceloInOfficeA = marcelo_index(officeA(i));
    rakeshInOfficeB = rakesh_index(officeB(i));
    A(i+numPairs+numOffices, [marceloInOfficeA, rakeshInOfficeB]) = 1;
end
b(numOffices+1:numOffices+2*numPairs) = ones(2*numPairs,1);

使用 intlinprog 求解

问题表示为一个线性目标函数

min -c'*x

受以下线性约束

Aeq*x = beq

A*x <= b

所有变量均为二元变量

您已经创建 A、b、Aeq 和 beq 条目。现在设定目标函数。

f = -c;

为了确保变量是二元变量，将下界设为 0，上界设为 1，并设置 intvars 来表示所有变量。

lb = zeros(size(f));
ub = lb + 1;
intvars = 1:length(f);

调用 intlinprog 以求解问题。

[x,fval,exitflag,output] = intlinprog(f,intvars,A,b,Aeq,beq,lb,ub);

LP:                Optimal objective value is -33.868852.                                           

Cut Generation:    Applied 1 Gomory cut.                                                            
                   Lower bound is -33.836066.                                                       
                   Relative gap is 0.00%.                                                          


Optimal solution found.

Intlinprog stopped at the root node because the objective value is within a gap tolerance of the optimal value,
options.AbsoluteGapTolerance = 0 (the default value). The intcon variables are integer within tolerance,
options.IntegerTolerance = 1e-05 (the default value).

查看解 - 哪个人分得了哪间办公室？

numPeople = 7; office = cell(numPeople,1);
for i=1:numPeople
    office{i} = find(x(i:numPeople:end)); % people index in office
end

people = {'Mary Ann', 'Marjorie','  Tom   ',' Peter  ','Marcelo ',' Rakesh '};
for i=1:numPeople
    if isempty(office{i})
        name{i} = ' empty  ';
    else
        name{i} = people(office{i});
    end
end

printofficeassign(name);
title('Solution of the Office Assignment Problem');

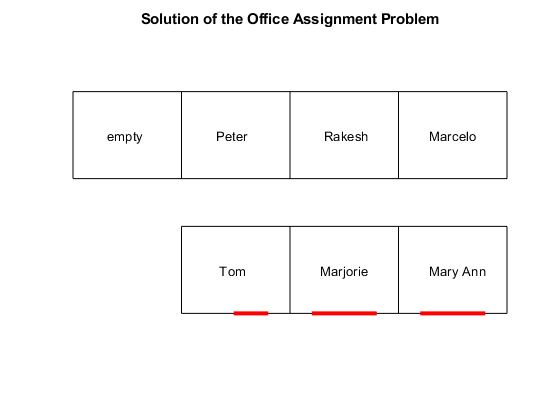
解质量

对于这个问题，通过最大化 -fval 的值来满足按资历排序的偏好。exitflag = 1 表明 intlinprog 收敛到一个最优解。输出结构给出了求解过程的信息，例如探索了多少个节点，以及分支计算中下界和上界之间的差距。在这种情况下，没有生成分支定界节点，这意味着问题无需分支定界步骤即可解决。差距为 0，表示解是最优的，内部计算的目标函数的下界和上界之间没有差异。

fval,exitflag,output

fval = -33.8361

exitflag = 1

output = struct with fields:
        relativegap: 0
        absolutegap: 0
      numfeaspoints: 1
           numnodes: 0
    constrviolation: 0
            message: 'Optimal solution found.↵↵Intlinprog stopped at the root node because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 0 (the default value). The intcon variables are integer within tolerance, options.IntegerTolerance = 1e-05 (the default value).'