基于问题通过二次规划进行投资组合优化
此示例说明如何使用基于问题的方法来求解投资组合优化问题。有关基于求解器的方法,请参阅基于求解器的投资组合优化问题的二次规划。
二次模型
假设一个投资组合包含  种不同资产。资产回报率
种不同资产。资产回报率  是随机变量,预期值为
是随机变量,预期值为 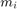 。问题是在指定的最低预期回报率约束下,找出在每项资产
。问题是在指定的最低预期回报率约束下,找出在每项资产  上的投资比例
上的投资比例  为多少,才能将风险降至最低。
为多少,才能将风险降至最低。
让 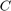 表示资产回报率的协方差矩阵。
表示资产回报率的协方差矩阵。
经典的均值-方差模型是在一组约束条件下最小化投资组合风险,风险可由下式衡量
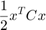
其中约束如下:
预期回报率不应低于投资者期望的最低投资组合回报率  ,
,
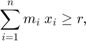
投资组合比例  的总和应为 1,
的总和应为 1,

而且作为比例(或百分比),它们应为介于 0 和 1 之间的数字,
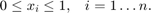
由于最小化投资组合风险的目标函数是二次型的,而约束是线性的,因此该优化问题是二次规划,即 QP。
225 项资产问题
现在让我们求解包含 225 项资产的 QP。该数据集来自 OR-Library [Chang, T.-J., Meade, N., Beasley, J.E. and Sharaiha, Y.M., "Heuristics for cardinality constrained portfolio optimisation" Computers & Operations Research 27 (2000) 1271-1302]。
我们加载该数据集,然后为基于问题的方法设置约束。在此数据集中,回报率 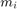 的范围在 -0.008489 和 0.003971 之间;我们在两者之间选择一个期望的回报率
的范围在 -0.008489 和 0.003971 之间;我们在两者之间选择一个期望的回报率  ,例如 0.002 (0.2%)。
,例如 0.002 (0.2%)。
加载存储在 MAT 文件中的数据集。
load('port5.mat','Correlation','stdDev_return','mean_return')
基于相关矩阵计算协方差矩阵。
Covariance = Correlation .* (stdDev_return * stdDev_return');
nAssets = numel(mean_return); r = 0.002; % number of assets and desired return
创建优化问题、目标和约束
创建一个要最小化的优化问题。
portprob = optimproblem;
使用 nAssets 个元素创建一个优化向量变量 'x'。此变量表示投资于每项资产的财富比例,因此应介于 0 和 1 之间。
x = optimvar('x',nAssets,'LowerBound',0,'UpperBound',1);
目标函数是 1/2*x'*Covariance*x。将此目标包含在问题中。
objective = 1/2*x'*Covariance*x; portprob.Objective = objective;
变量的总和是 1,表示投入整个投资组合。将此项表达为一个约束,并将其加入问题中。
sumcons = sum(x) == 1; portprob.Constraints.sumcons = sumcons;
平均回报必须大于 r。将此项表达为一个约束,并将其加入问题中。
averagereturn = dot(mean_return,x) >= r; portprob.Constraints.averagereturn = averagereturn;
求解 225 项资产问题
设置一些选项,并调用求解器。
设置选项以打开迭代输出,并设置更严格的最优性终止容差。
options = optimoptions('quadprog','Display','iter','TolFun',1e-10);
调用求解器并测量挂钟时间。
tic
[x1,fval1] = solve(portprob,'Options',options);
toc
Solving problem using quadprog.
Iter Fval Primal Infeas Dual Infeas Complementarity
0 7.212813e+00 1.227500e+02 1.195948e+00 2.217295e-03
1 8.160874e-04 3.615084e-01 3.522160e-03 2.250524e-05
2 7.220766e-04 3.592574e-01 3.500229e-03 3.378157e-05
3 4.309434e-04 9.991108e-02 9.734292e-04 2.790551e-05
4 4.734300e-04 2.220446e-16 6.661338e-16 4.242216e-06
5 4.719034e-04 1.110223e-16 3.139849e-16 8.002618e-07
6 3.587475e-04 2.220446e-16 2.602085e-18 3.677066e-07
7 3.131814e-04 4.440892e-16 2.168404e-18 9.586695e-08
8 2.760174e-04 5.551115e-16 2.114194e-18 1.521063e-08
9 2.345751e-04 4.440892e-16 1.138412e-18 4.109608e-09
10 2.042487e-04 4.440892e-16 1.029992e-18 6.423267e-09
11 1.961775e-04 4.440892e-16 9.757820e-19 6.068329e-10
12 1.949281e-04 0.000000e+00 9.757820e-19 4.279951e-12
Minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.
Elapsed time is 0.115332 seconds.
绘制结果。
plotPortfDemoStandardModel(x1.x)
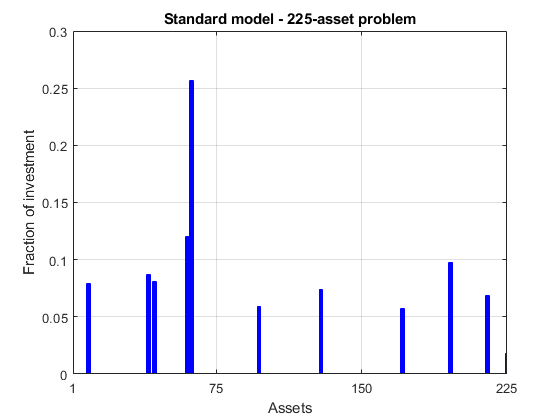
具有组约束的 225 项资产问题
我们现在向模型增加组约束,即要求投资者 30% 的资金必须投资于资产 1 至 75,30% 投资于资产 76 至 150,30% 投资于资产 151 至 225。每组资产可以是不同行业,例如技术、汽车和制药。实现此新要求的约束是

向现有等式添加组约束。
grp1 = sum(x(1:75)) >= 0.3; grp2 = sum(x(76:150)) >= 0.3; grp3 = sum(x(151:225)) >= 0.3; portprob.Constraints.grp1 = grp1; portprob.Constraints.grp2 = grp2; portprob.Constraints.grp3 = grp3;
调用求解器并测量挂钟时间。
tic
[x2,fval2] = solve(portprob,'Options',options);
toc
Solving problem using quadprog.
Iter Fval Primal Infeas Dual Infeas Complementarity
0 7.212813e+00 1.227500e+02 3.539920e-01 5.253824e-03
1 7.004556e-03 2.901399e+00 8.367185e-03 2.207460e-03
2 9.181962e-04 4.095630e-01 1.181116e-03 3.749424e-04
3 7.515047e-04 3.567918e-01 1.028932e-03 3.486333e-04
4 4.238346e-04 9.005778e-02 2.597127e-04 1.607718e-04
5 3.695008e-04 1.909891e-04 5.507829e-07 1.341881e-05
6 3.691407e-04 6.146337e-07 1.772508e-09 6.817457e-08
7 3.010636e-04 7.691892e-08 2.218222e-10 1.837302e-08
8 2.669065e-04 1.088252e-08 3.138350e-11 5.474712e-09
9 2.195767e-04 8.122576e-10 2.342425e-12 2.814320e-08
10 2.102910e-04 2.839771e-10 8.189465e-13 1.037476e-08
11 2.060985e-04 6.713785e-11 1.936135e-13 2.876950e-09
12 2.015107e-04 7.771561e-16 9.215718e-19 1.522226e-10
13 2.009670e-04 6.661338e-16 1.029992e-18 5.264375e-13
Minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.
Elapsed time is 0.115345 seconds.
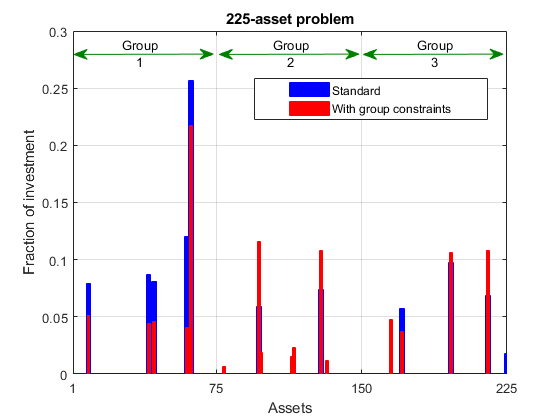
绘制结果,叠加在先前问题的结果上。
plotPortfDemoGroupModel(x1.x,x2.x);
迄今为止结果摘要
我们从第二个条形图中看到,由于存在额外的组约束,与第一个投资组合相比,现在投资组合在三个资产组中的分布更均匀。这种强加的多样化也导致风险略微增加,这是通过目标函数来测量的(请参阅两次运行的迭代输出中最后一次迭代的标记为“f(x)”的列)。
使用随机数据的 1000 项资产问题
为了说明求解器如何处理更大型的问题,我们将使用包含 1000 项资产的随机生成的数据集。我们使用 MATLAB® 中的 gallery 函数生成随机相关矩阵(对称、半正定矩阵,对角线元素为 1)。
重置随机流以实现可再现性。
rng(0,'twister'); nAssets = 1000; % desired number of assets
创建随机数据
生成 -0.1 到 0.4 之间的回报率均值数据。
a = -0.1; b = 0.4;
mean_return = a + (b-a).*rand(nAssets,1);
r = 0.15; % desired return
生成 0.08 到 0.6 之间的回报率标准差数据。
a = 0.08; b = 0.6; stdDev_return = a + (b-a).*rand(nAssets,1);
加载使用 Correlation = gallery('randcorr',nAssets) 生成的相关矩阵。(生成这样大小的相关矩阵需要一段时间,因此请加载预先生成的矩阵。)
load('correlationMatrixDemo.mat','Correlation');
基于相关矩阵计算协方差矩阵。
Covariance = Correlation .* (stdDev_return * stdDev_return');
创建优化问题、目标和约束
创建一个要最小化的优化问题。
portprob2 = optimproblem;
使用 nAssets 个元素创建优化向量变量 'x'。
x = optimvar('x',nAssets,'LowerBound',0,'UpperBound',1);
将目标函数加入问题中。
objective = 1/2*x'*Covariance*x; portprob2.Objective = objective;
加入变量之和为 1 且平均回报大于 r 的约束。
sumcons = sum(x) == 1; portprob2.Constraints.sumcons = sumcons; averagereturn = dot(mean_return,x) >= r; portprob2.Constraints.averagereturn = averagereturn;
求解 1000 项资产问题
调用求解器并测量挂钟时间。
tic
x3 = solve(portprob2,'Options',options);
toc
Solving problem using quadprog.
Iter Fval Primal Infeas Dual Infeas Complementarity
0 2.142849e+01 5.490000e+02 3.031839e+00 5.210929e-03
1 9.378552e-03 6.439102e+00 3.555978e-02 6.331676e-04
2 1.128129e-04 3.705915e-03 2.046582e-05 1.802721e-05
3 1.118804e-04 1.852958e-06 1.023291e-08 1.170562e-07
4 8.490176e-05 7.650016e-08 4.224702e-10 7.048637e-09
5 3.364597e-05 4.440892e-16 2.574980e-18 1.037370e-09
6 1.980189e-05 8.881784e-16 9.419006e-19 8.465558e-11
Minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.
Elapsed time is 5.070618 seconds.
摘要
此示例说明如何使用基于问题的方法来求解投资组合优化问题,并展示求解不同规模的二次问题的算法运行时间。
通过使用 Financial Toolbox™ 中专为投资组合优化而设计的功能,可以进行更详细的分析。