Battery Module Geometry

Open Live Script

This example shows how to create a battery module geometry consisting of nine cells, connectors at both ends, and the casing. The geometry has an air gap between the cells and the casing.

Creating the battery module geometry requires these steps:

Create 2-D geometries representing the sections ("footprints") of the cells and connectors, and the top, bottom, and walls of the casing.
Extrude the 2-D geometries into 3-D
Mirror and combine the sections of the geometry into the 3-D battery module geometry.

This example uses SI units of measurement.

Specify Dimensions

Define the key geometric parameters of a 18650 Li-ion battery cell and module. All geometric dimensions are in meters.

cellDiameter = 18/1000;
cellLength = 65/1000;
interCellGap = 1/1000;
connectorThickness = 0.5/1000;
casingThickness = 1/1000;

Create 2-D Geometries

The create2DGeometry function takes key geometric dimensions as inputs and returns three 2-D geometric sections: cells and connectors, top and bottom casings, and casing side walls.

function [gm2DCellConnector, ...
          gmCasingCap2D, ...
          gmCasingWalls2D, ...
          referencePoints] = ...
          create2DGeometry(D,gap,casingThickness)

widthConnector = D;
% Three cells and gaps in between
lengthConnector = 3*D + 4*gap;
connectorX = [-widthConnector/2, ...
               widthConnector/2, ...
               widthConnector/2, ...
              -widthConnector/2];
connectorY = [-lengthConnector/2, ...
              -lengthConnector/2, ...
               lengthConnector/2, ...
               lengthConnector/2];
R1 = [3 4 connectorX connectorY];
R2 = [3 4 connectorX - D - 1*gap connectorY];
R3 = [3 4 connectorX + D + 1*gap connectorY];

topConnectorX = widthConnector/2 + D + 1*gap;
topConnectorY = lengthConnector/2 + 4*gap;
R4 = [3 4 -topConnectorX ...
           topConnectorX ...
           topConnectorX ...
          -topConnectorX...
           lengthConnector/2 ...
           lengthConnector/2 ...
           topConnectorY ...
           topConnectorY];

wallGap = 1*gap;
wallX = topConnectorX + wallGap;

RinnerWall = [3 4 -wallX wallX wallX -wallX ...
                  -lengthConnector/2 - wallGap ...
                  -lengthConnector/2 - wallGap ...
                   topConnectorY + wallGap ...
                   topConnectorY + wallGap];
RouterWall = [3 4 -wallX - casingThickness ...
                   wallX + casingThickness ...
                   wallX + casingThickness ...
                  -wallX - casingThickness ...
                  -lengthConnector/2 - wallGap - ...
                                       casingThickness ...
                  -lengthConnector/2 - wallGap - ...
                                       casingThickness ...
                   topConnectorY + wallGap + ...
                                   casingThickness ...
                   topConnectorY + wallGap + ...
                                   casingThickness];

% Define circles representing cells.
numCells = 9;
pitch = D + 1*gap;
[xc,yc] = meshgrid(-pitch:pitch:pitch);
C = ones(numel(R1),numCells);
C(2,:) = xc(:);
C(3,:) = yc(:);
C(4,:) = D/2;
C(5:end,:) = 0;

% Construct the geometry of
% the cells and connectors section.
ns = ["R1","R2","R3","R4"];
ns = [ns, "C" + string(1:9)];
sf = "(R1+R2+R3+R4)";
sf = sf+"+"+join("C"+string(1:9),"+");
gd = [R1' R2' R3' R4' C];

gm2DCellConnector = fegeometry(decsg(gd,sf,ns));
gmCasingCap2D  = fegeometry(decsg(RouterWall'));
gmCasingWalls2D = fegeometry(decsg([RouterWall' RinnerWall'], ...
                                   "Ro-Rw",["Ro" "Rw"]));


referencePoints.Cell = [xc(:) yc(:) 0*xc(:)];

RwX = RinnerWall(3:6);
RwY= RinnerWall(7:end);
referencePoints.Casing = [RwX(1) 0 0
                          RwX(3) 0 0
                          0 RwY(1) 0
                          0 RwY(3) 0];

end

Create the 2-D geometries by using the create2DGeometry function.

[gm2DCellConnector, ...
 gmCasingCap2D, ...
 gmCasingWalls2D, ...
 referencePoints] = ...
create2DGeometry(cellDiameter, ...
                 interCellGap, ...
                 casingThickness);

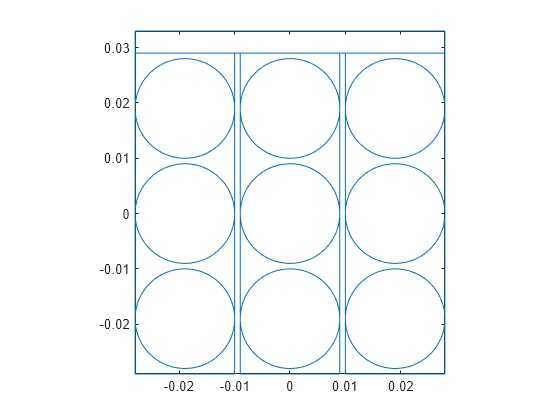
Plot the 2-D geometry representing the cells and connectors, gm2DCellConnector. When you extrude the geometry in the next step, the circles in this geometry extrude to form the cells, and the rectangles extrude to form the connectors.

figure
pdegplot(gm2DCellConnector)

Figure contains an axes object. The axes object contains an object of type line.

Extrude Geometry

Extrude the gm2DCellConnector geometry to the connector thickness.

gm3DConnector = extrude(gm2DCellConnector,connectorThickness);

Find face IDs of the circular faces at the top of the extruded cells.

cellEndFaces = nearestFace(gm3DConnector, ...
                           referencePoints.Cell + ...
                           [0,0,connectorThickness])

cellEndFaces = 1×9

    36    37    38    39    40    41    42    43    44

Plot the extruded geometry with the face labels to see these face IDs.

pdegplot(gm3DConnector,FaceLabels="on")
view([0 90])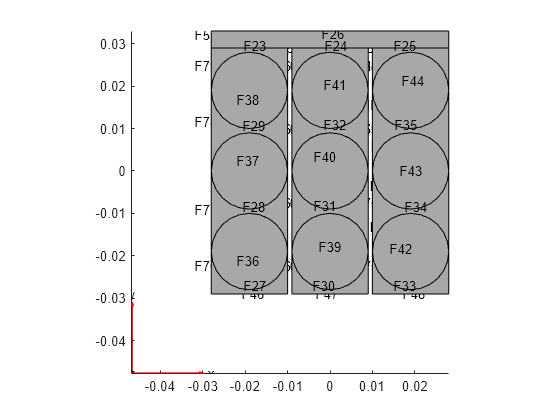

Figure contains an axes object. The axes object contains 6 objects of type quiver, text, patch, line.

Extrude cells to the half the required length. Later, you reflect the geometry to obtain the other half.

gm3DConnectorCellsHalf = extrude(gm3DConnector, ...
                                 cellEndFaces, ...
                                 cellLength/2);

Extrude the 2-D geometry of the casing side walls, gmCasingWalls2D, to a length that covers the cells and connectors at both ends.

gm3DCasing = extrude(gmCasingWalls2D, ...
                     2*connectorThickness + ...
                     cellLength + ...
                     2*casingThickness);

Plot the resulting geometry representing the casing side walls.

pdegplot(gm3DCasing,FaceLabels="on",FaceAlpha=0.3)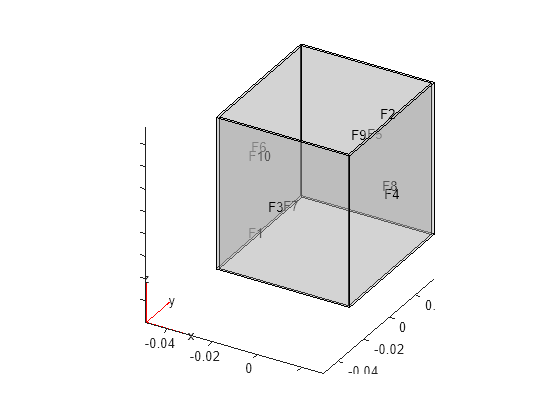

Figure contains an axes object. The axes object contains 6 objects of type quiver, text, patch, line.

Extrude the 2-D geometry of the top and bottom caps of the casing, gmCasingCap2D.

gm3DCap = extrude(gmCasingCap2D,casingThickness);

Plot the resulting casing caps.

pdegplot(gm3DCap,FaceLabels="on",FaceAlpha=0.3)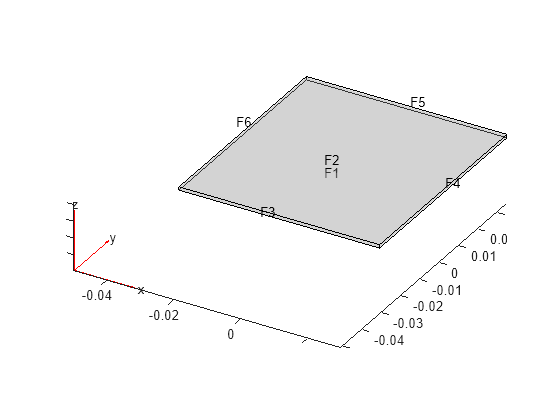

Figure contains an axes object. The axes object contains 6 objects of type quiver, text, patch, line.

Mirror Cells and Assemble Geometry

Now you have all the components for the 3-D geometry representing a battery module. The next step is to mirror the geometry gm3DConnectorCellsHalf, and then complete the module by placing all the components at the required positions.

The assemble3DGeometry function takes the three geometries and some key dimensions as inputs, mirrors the cells, and assembles the geometry of the battery module. The assemble3DGeometry function also returns various domain IDs as a structural array to use for setting up the thermal analysis model. This function uses the helper function, findCellID, to find the domain IDs of the cells by a given point inside the cell.

function [gmAssembled,domainIDs] = ...
    assemble3DGeometry(gm3DHalf,gmCasing,gmCap, ...
                       refPoints,cellLength, ...
                       connectorThickness, ...
                       casingThickness)
% Generate linear mesh to recreate the geometry
% from the mesh with desired subdomains:
% nine cells, two connectors, and three casings.
gm3DHalf = generateMesh(gm3DHalf, ...
                        GeometricOrder="linear");
gmCap = generateMesh(gmCap, ...
                     GeometricOrder="linear");
gmCasing = generateMesh(gmCasing, ...
                        GeometricOrder="linear");

% Find the cell IDs of various cell volumes.
cellCenters = refPoints.Cell + [0 0 cellLength/4];
cellDomainIDs = findCellID(gm3DHalf,cellCenters);

domainIDs.Cells = 1:numel(cellDomainIDs);
% Reconstruct the geometry from the mesh with cells.
msh = gm3DHalf.Mesh;
% Map elements in each half cell to domains 1 to 9.
% Leave the remaining elements, belonging to
% the connector, in domain 10.
elem2regionID = 10*ones(1,size(msh.Elements,2));
for i = domainIDs.Cells
    eIDs = findElements(msh,"region", ...
                        Cell=cellDomainIDs(i));
    elem2regionID(eIDs) = i;
end

elemsBottomHalf = msh.Elements';
nodesBottomHalf = msh.Nodes';

% Move the bottom half cell to below z = 0 plane.

maxZ = max(nodesBottomHalf(:,3));
nodesBottomHalf(:,3) = nodesBottomHalf(:,3) - maxZ;

% Mirror the bottom half to complete the cell
% and connector geometry.
nodesTopHalf = nodesBottomHalf;
nodesTopHalf(:,3) = -1*nodesTopHalf(:,3);
elemsTopHalf = elemsBottomHalf + size(nodesBottomHalf,1);
elemsTopHalf(:,[2,3]) = elemsTopHalf(:,[3,2]);

elemsCombined = [elemsBottomHalf; elemsTopHalf];
nodesCombined = [nodesBottomHalf; nodesTopHalf];
elem2regionIDTop = elem2regionID;
elem2regionIDTop(elem2regionID==10) = 11;
elem2regionID = [elem2regionID, elem2regionIDTop];
domainIDs.Connector = [10 11];

% Remove duplicate nodes at the mirror plane z = 0.
[nodesCombined,~,ic] = ...
    uniquetol(nodesCombined,1e-14,ByRows=true);
elemsCombined = ic(elemsCombined);

% Transform the geometry for the top and
% bottom casing caps and add them to elements.
domainIDs.Casing = [12 13 14];
[nodesCombined,elemsCombined,elem2regionID] = ...
    transformAddGeometry(nodesCombined,elemsCombined,gmCap, ...
                         [0,0,-connectorThickness- ...
                          2*casingThickness-cellLength/2], ...
                         elem2regionID,domainIDs.Casing(1));
[nodesCombined,elemsCombined,elem2regionID] = ...
    transformAddGeometry(nodesCombined,elemsCombined,gmCap, ...
                         [0,0,connectorThickness+ ...
                         casingThickness+cellLength/2], ...
                         elem2regionID,domainIDs.Casing(2));
% Add the casing side wall elements.
[nodesCombined,elemsCombined,elem2regionID] = ...
    transformAddGeometry(nodesCombined,elemsCombined,gmCasing, ...
                         [0,0,-cellLength/2- ...
                         connectorThickness- ...
                         casingThickness], ...
                         elem2regionID,domainIDs.Casing(3));

gmAssembled = fegeometry(nodesCombined,elemsCombined,elem2regionID);
end

Call the assemble3DGeometry function to assemble the geometry and remove the material between the battery cells.

[gmAssembled,domainIDs] = ...
    assemble3DGeometry(gm3DConnectorCellsHalf, ...
                       gm3DCasing, ...
                       gm3DCap, ...
                       referencePoints, ...
                       cellLength, ...
                       connectorThickness, ...
                       casingThickness);

Plot the resulting geometry.

figure
pdegplot(gmAssembled,FaceAlpha=0.25,CellLabels="on")

Figure contains an axes object. The axes object contains 6 objects of type quiver, text, patch, line.

Helper Functions

The transformAddGeometry function transforms the geometry for the casing caps and adds them to elements.

function [n,e,elem2regionID] = ...
    transformAddGeometry(n,e,gm,translate, ...
                         elem2regionID,assignedID)
nodeOffset = size(n,1);
n = [n; gm.Mesh.Nodes' + translate];
e = [e; gm.Mesh.Elements' + nodeOffset];
elem2regionID = [elem2regionID ...
                 assignedID*ones(1,size(gm.Mesh.Elements,2))];
end

The findCellID function uses a point inside the cell to identify the cell ID.

function fID = findCellID(gm,pt)

msh = gm.Mesh;
doms = cell(1,gm.NumCells);

for k=1:gm.NumCells
    doms{k} = findElements(msh,"region",Cell=k);
end
% Convert the mesh to triangulation and ID of the cell
% containing the point.
tr = triangulation(msh.Elements',msh.Nodes');
fID = zeros(1,size(pt,1));
for i = 1:size(pt,1)
    zz = pointLocation(tr,pt(i,:));
    mem = cellfun(@(x)ismember(zz,x),doms);
    fID(i) = find(mem,1,"first");
end
if isempty(fID)
    error("Outside of all domains");
end
end