Compute the Maxwell stress tensor at nodal locations, and then interpolate it to the specified grid.
Create a square geometry.
Create an femodel object for magnetostatic analysis. Include the square geometry.
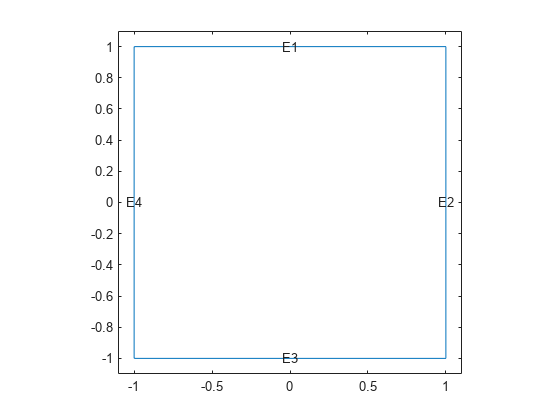
Plot the geometry with edge labels.
Specify the vacuum permeability in the SI system of units.
Specify the relative permeability of the material.
Apply the magnetic potential boundary conditions on the sides of the square.
Specify the current density for the entire geometry.
Generate the mesh. This assignment updates the mesh stored in the Geometry property of the model.
Solve the model. The solution R is a MagnetostaticResults object. It does not include the Maxwell stress tensor by default.
R =
MagnetostaticResults with properties:
MagneticPotential: [1529×1 double]
MagneticField: [1×1 FEStruct]
MagneticFluxDensity: [1×1 FEStruct]
Mesh: [1×1 FEMesh]
Generate the Maxwell stress tensor and store it as a property of the results object R.
R =
MagnetostaticResults with properties:
MagneticPotential: [1529×1 double]
MagneticField: [1×1 FEStruct]
MagneticFluxDensity: [1×1 FEStruct]
Mesh: [1×1 FEMesh]
MaxwellStressTensor: [2×2×1529 double]
Interpolate the resulting Maxwell stress tensor to a grid covering the central portion of the geometry, for x and y from -0.5 to 0.5.
Alternatively, you can specify the grid by using a matrix of query points.