meshQuality
Evaluate shape quality of mesh elements
Description
Q = meshQuality(___,"aspect-ratio")"aspect-ratio" after
any of the previous syntaxes.
Examples
Input Arguments
Output Arguments
Algorithms
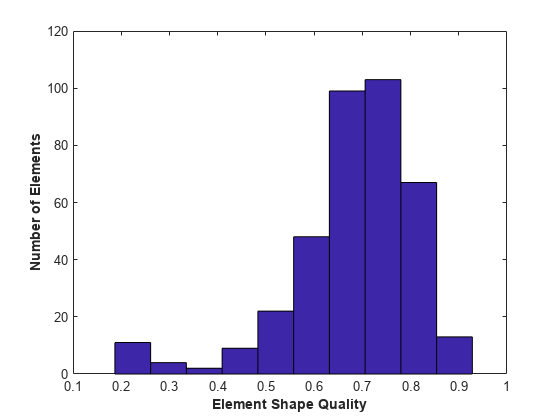
By default, meshQuality calculates the shape quality of a
triangular mesh element as follows:
Here, A is the area of the triangle, and li are the edge lengths of the triangle.
meshQuality calculates the shape quality of a tetrahedral mesh
element as follows:
Here, V is the volume of the tetrahedron, li are the edge lengths, and Ak are the areas of the triangular faces.
When you use the aspect-ratio argument,
meshQuality calculates the quality of a triangular mesh element
as follows:
Here, lmax is the maximal edge length of the triangle.
The aspect-ratio quality of a tetrahedral mesh element is:
Here, lmax is the maximal edge length of the tetrahedron, and Amax is the area of the largest face of the tetrahedron:
References
[1] Knupp, Patrick M. "Matrix Norms & the Condition Number: A General Framework to Improve Mesh Quality via Node-Movement." In Proceedings, 8th International Meshing Roundtable. Lake Tahoe, CA, October 1999: 13-22.
[2] Shewchuk, Jonathan R. "What Is a Good Linear Element? Interpolation, Conditioning, and Quality Measures." In Proceedings, 11th International Meshing Roundtable. Ithaca, NY, September 2002: 115-126.
Version History
Introduced in R2018a