arrayfactor
Description
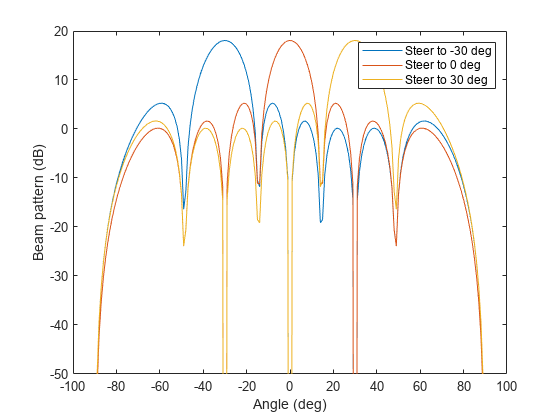
af = arrayfactor(pos,ang)af for an array of elements located at
positions pos and arrival directions ang. See
Element and Array Radiation and Response Patterns
for a discussion of array factors and array responses.
Examples
Input Arguments
Output Arguments
References
[1] Van Trees, Harry L. Detection, Estimation, and Modulation Theory. 4: Optimum Array Processing. Wiley, 2002.
[2] Johnson, Don H. and D. Dudgeon. Array Signal Processing. Englewood Cliffs, NJ: Prentice Hall, 1993.
[3] Van Veen, B.D. and K. M. Buckley. “Beamforming: A versatile approach to spatial filtering”
Extended Capabilities
Version History
Introduced in R2022a