Main Content

sidelobelevel

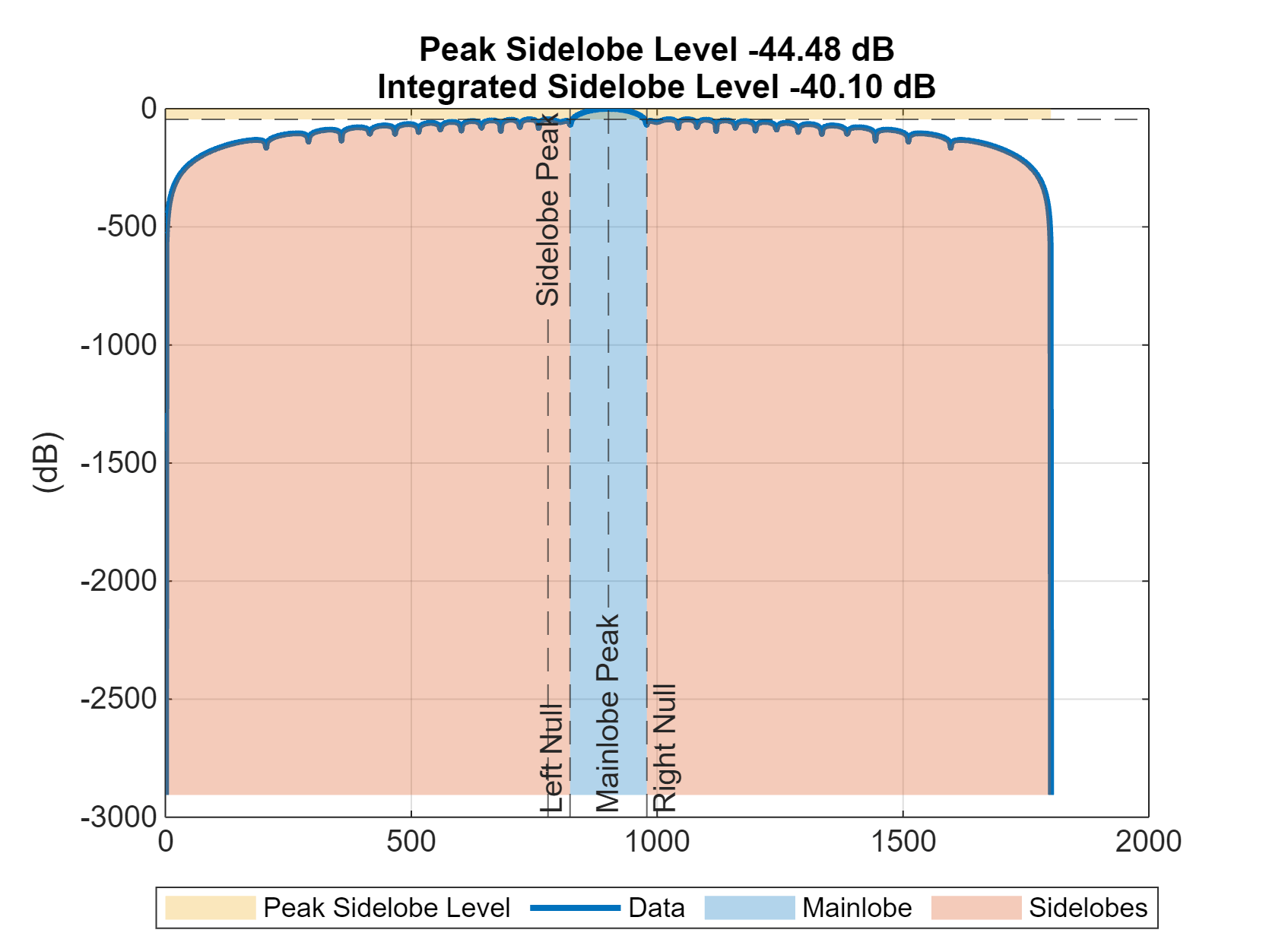
Peak and integrated side-lobe levels

Since R2024b

collapse all in page

    Syntax

    psl = sidelobelevel(Y)
    psl = sidelobelevel(Y,SmoothingFactor=sf)
    psl = sidelobelevel(Y,MaxRipple=mr)
    [isl,isl] = sidelobelevel(Y,___)
    sidelobelevel(Y,___)

    Description

    sidelobelevel returns the peak sidelobe level of a set of vector data that can represent, for example, autocorrelation functions, array beam patterns, or matched filter output, or any data that can have a peak-and-lobe shape. The data must be dB-scaled data. The function can optionally return integrated sidelobe levels.

    psl = sidelobelevel(Y) calculates the peak sidelobe level (PSL), psl, from an N-element vector Y containing dB values. The input Y may represent data from an autocorrelation function, array beam pattern, matched filter output, or other dB-scaled data.

    example

    psl = sidelobelevel(Y,SmoothingFactor=sf) applies a smoothing window to the data with size factor sf. The smoothing window size factor can range from 0 to 1. Smaller values result in less smoothing, while values closer to 1 result in more smoothing. The default is 0 (no smoothing). Smoothing utilizes a moving Gaussian-weighted window to reduce local variations in Y improving accurate identification of the mainlobe and sidelobes in the presence of noise and distortion.

    psl = sidelobelevel(Y,MaxRipple=mr) specifies the maximum ripple height mr, as a non-negative scalar. Ripples smaller than mr dB are disregarded in mainlobe and sidelobe detection. The default mr value is 0 dB.

    [isl,isl] = sidelobelevel(Y,___) also returns the integrated sidelobe level isl (ISL).

    sidelobelevel(Y,___) produces a plot of the input data, Y, highlighting the estimated mainlobe and sidelobe regions.

    Examples

    collapse all

    Open Live Script

    Compute the peak and integrated sidelobe levels of the array pattern of a 32-element uniform linear array (ULA) of cosine antenna elements. The array operating frequency is 300 HMz. Apply a Hamming taper to the array.

    N = 32;
fc = 300e6;

    Compute the operating wavelength.

    lambda = freq2wavelen(fc);

    Construct the ULA using cosine antenna elements.

    element = phased.CosineAntennaElement(CosinePower=[8,8]);
ula = phased.ULA(N,lambda/2,'Element',element,'Taper',hamming(N));

    Compute the array pattern.

    az = -90:0.1:90;
pat = pattern(ula,fc,az,0,'Type','powerdb', ...
     'CoordinateSystem','rectangular','Normalize',true);

    Compute and display the array sidelobe levels.

    [psl,isl]=sidelobelevel(pat)
    psl = 
-44.4832

    isl = 
-40.1004

    sidelobelevel(pat)

    Figure contains an object of type phased.internal.sidelobelevelchart.

    Input Arguments

    collapse all

    Vector data, specified as an N-element real-valued vector. The Y vector can represent various sources of data such as autocorrelation functions, array beam patterns, matched filter outputs, or other dB-scaled characteristic. Units are in dB.

    Data Types: single | double

    Smoothing factor, specified as a nonnegative scalar between 0 and 1. Use this argument with the SmoothingFactor Name-Value pair. Units are dimensionless.

    Example: SmoothingFactor=0.5

    Data Types: single | double

    Maximum ripple, specified as nonnegative scalar. Use this argument with the MaxRipple Name-Value pair. Units are in dB.

    Example: MaxRipple = 10

    Data Types: single | double

    Output Arguments

    collapse all

    Peak sidelobe level, returned as a scalar. Units are in dB.

    Integrated sidelobe level, returned as a scalar. Units are in dB.

    More About

    collapse all

    Identify peak and sidelobes

    The function performs these operations to find the sidelobe and the mainlobe regions in data:

    1. Identify peaks within Y.

    2. Designate the highest peak as the mainlobe peak. In cases where multiple peaks share the highest value, select the peak with the lowest index.

    3. Identify the main lobe's left boundary as the lowest point between the mainlobe peak and the next peak to its left. If no left peak exists, the mainlobe extends to the first data point Y.

    4. Identify the main lobe's right boundary as the lowest point between the mainlobe peak and the next peak to its right. If no right peak exists, the mainlobe extends to the last data point Y.

    5. Designate data points outside of the mainlobe boundaries as belonging to the sidelobe region.

    Sidelobe Levels

    When the sidelobes and mainlobes are identified, the peak and integrated sidelobe levels can be calculated from the formulas below.

    The peak sidelobe level (PSL) is given by:

    PSL=10log10maxMy2maxSywherey=10YdB20.

    Ydb denotes dB values and y denotes magnitude values. maxS denotes the maximum of y over the (generally disjoint) sidelobe region S and maxM the denotes maximum of y over the continuous mainlobe region M.

    The integrated sidelobe level (ISL) is given by

    ISL=10log10intMy2intSy

    where intS denotes integration over the sidelobe region S and intM denotes integration over the mainlobe region M.

    Version History

    Introduced in R2024b