Main Content

uv2azel

Convert u/v coordinates to azimuth/elevation angles

collapse all in page

Syntax

AzEl = uv2azel(UV)

Description

AzEl = uv2azel(UV) converts the u/v space coordinates to their corresponding azimuth/elevation angle pairs.

example

Examples

collapse all

Open Live Script

Find the corresponding azimuth/elevation representation for u = 0.5 and v = 0. 

azel = uv2azel([0.5; 0])
azel = 2×1

   30.0000
         0

Input Arguments

collapse all

Angle in u/v space, specified as a two-row matrix. Each column of the matrix represents a pair of coordinates in the form [u; v]. Each coordinate is between –1 and 1, inclusive. Also, each pair must satisfy u2 + v2≤ 1.

Data Types: double

Output Arguments

collapse all

Azimuth and elevation angles, returned as a two-row matrix. Each column of the matrix represents an angle in degrees, in the form [azimuth; elevation]. The matrix dimensions of AzEl are the same as those of UV.

More About

collapse all

U/V Space

The u/v coordinates for the positive hemisphere x ≥ 0 can be derived from the phi and theta angles.

The relation between the two coordinates is

u=sinθcosϕv=sinθsinϕ

In these expressions, φ and θ are the phi and theta angles, respectively.

To convert azimuth and elevation to u and v use the transformation

u=coselsinazv=sinel

which is valid only in the range abs(az)≤=90.

The values of u and v satisfy the inequalities

−1≤u≤1−1≤v≤1u2+v2≤1

Conversely, the phi and theta angles can be written in terms of u and v using

tanϕ=v/usinθ=u2+v2

The azimuth and elevation angles can also be written in terms of u and v:

sinel=vtanaz=u1−u2−v2

Phi Angle, Theta Angle

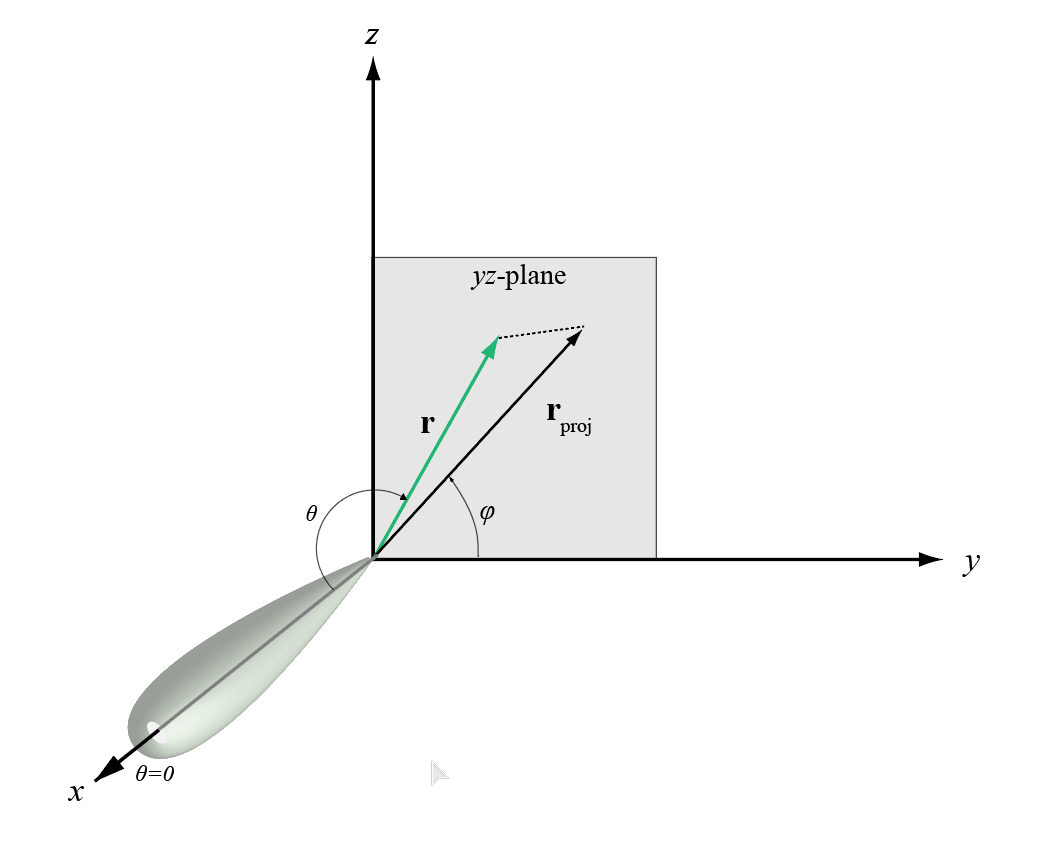
The phi angle (φ) is the angle from the positive y-axis to the vector’s orthogonal projection onto the yz plane. The angle is positive toward the positive z-axis. The phi angle is between 0 and 360 degrees. The theta angle (θ) is the angle from the x-axis to the vector itself. The angle is positive toward the yz plane. The theta angle is between 0 and 180 degrees.

The figure illustrates phi and theta for a vector that appears as a green solid line.

The coordinate transformations between φ/θ and az/el are described by the following equations

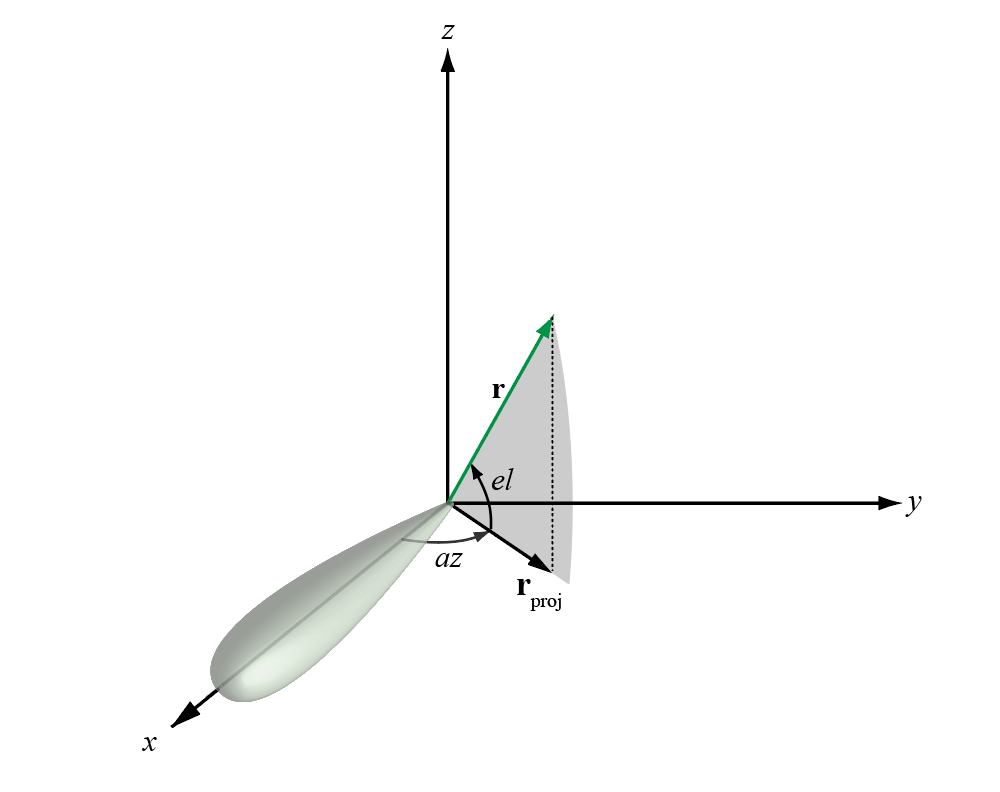
sinel=sinϕsinθtanaz=cosϕtanθcosθ=coselcosaztanϕ=tanel/sinaz

Azimuth Angle, Elevation Angle

The azimuth angle of a vector is the angle between the x-axis and the orthogonal projection of the vector onto the xy plane. The angle is positive in going from the x axis toward the y axis. Azimuth angles lie between –180 and 180 degrees. The elevation angle is the angle between the vector and its orthogonal projection onto the xy-plane. The angle is positive when going toward the positive z-axis from the xy plane. By default, the boresight direction of an element or array is aligned with the positive x-axis. The boresight direction is the direction of the main lobe of an element or array.

Note

The elevation angle is sometimes defined in the literature as the angle a vector makes with the positive z-axis. The MATLAB® and Phased Array System Toolbox™ products do not use this definition.

This figure illustrates the azimuth angle and elevation angle for a vector shown as a green solid line.

Extended Capabilities

Version History

Introduced in R2012a

See Also

Topics