Main Content

toccgh

Compute track probabilities using the CGH algorithm

Since R2021a

collapse all in page

Syntax

[pdt,pft,eft] = toccgh(pd,pfa)
[pdt,pft,eft] = toccgh(pd,pfa,Name,Value)
toccgh(___)

Description

[pdt,pft,eft] = toccgh(pd,pfa) computes track probabilities using the Common Gate History Algorithm. The algorithm uses a 2-out-of-3 track confirmation logic, where 2 hits must be observed in 3 updates for a track to be confirmed.

example

[pdt,pft,eft] = toccgh(pd,pfa,Name,Value) specifies additional options using name-value arguments. Options include the confirmation logic, the gate size in bins, and the gate growth sequence.

example

toccgh(___) with no output arguments plots the tracker operating characteristic (TOC), which is the probability of target track, pdt, as a function of the probability of false track, pft.

example

Examples

collapse all

Open Live Script

The tracker operating characteristic (TOC) curve is a plot of the probability of a target track as a function of the probability of a false track. Plot the TOC curves for three different values of signal-to-noise ratio (SNR) assuming a 2/3 confirmation logic and use a one-dimensional constant-velocity Kalman filter to generate the tracker gate growth sequence.

Compute the probability of detection and the probability of false alarm for SNR values of 3, 6, and 9 dB. Assume a coherent receiver with a nonfluctuating target. Generate 20 probability-of-false-alarm values logarithmically equally spaced between 10-10 and 10-3 and calculate the corresponding probabilities of detection.

SNRdB = [3 6 9];

[pd,pfa] = rocsnr(SNRdB,'SignalType','NonfluctuatingCoherent', ...
    'NumPoints',20,'MaxPfa',1e-3);

Compute and plot the TOC curves and the corresponding receiver operating characteristic (ROC) curves.

toccgh(pd,pfa)

Figure Operating Characteristics contains 2 axes objects. Axes object 1 with title Receiver Operating Characteristic (ROC) Curve, xlabel P_{FA}, ylabel P_D contains 63 objects of type line, text. These objects represent ROC 1, ROC 2, ROC 3. Axes object 2 with title Tracker Operating Characteristic (TOC) Curve, xlabel P_{FT}, ylabel P_{DT} contains 63 objects of type line, text.

Open Live Script

Compute the probability of target track, the probability of false track, and the expected number of false tracks corresponding to a probability of detection of 0.9, a probability of false alarm of 10-6, and a 3-of-5 track confirmation logic.

pd = 0.9;
pfa = 1e-6;
logic = [3 5];

Use a modified version of the default one-dimensional constant-velocity Kalman filter to generate the tracker gate growth sequence. Specify an update time of 0.3 second and a maximum target acceleration of 20 meters per square second.

KFpars = {'UpdateTime',0.3,'MaxAcceleration',20};

Compute the probabilities and the expected number of false tracks.

[pdf,pft,eft] = toccgh(pd,pfa,'ConfirmationThreshold',logic,KFpars{:})
pdf = 
0.9963

pft = 
2.1555e-19

eft = 
1
Open Live Script

Use the common gate history algorithm to compute the probability of target track and the probability of track for a probability of detection of 0.5 and a probability of false alarm of 10-3. Use a custom gate growth sequence and a confirmation threshold of 3/4.

pd = 0.5;
pfa = 1e-3;

cp = [3 4];
gs = [21 39 95 125];

Compute the probabilities.

[pdf,pft] = toccgh(pd,pfa,'ConfirmationThreshold',cp, ...
    'GateGrowthSequence',gs)
pdf = 
0.5132

pft = 
9.9973e-07
Open Live Script

Investigate how receiver operating characteristic (ROC) and tracker operating characteristic (TOC) curves change with the probability of false alarm.

Compute probability-of-detection and signal-to-noise-ratio (SNR) values corresponding to probabilities of false alarm of 10-4 and 10-6. Assume a coherent receiver with a nonfluctuating target. Plot the resulting ROC curves. Use larger markers to denote a larger SNR value.

pfa = [1e-4 1e-6];
[pd,SNRdB] = rocpfa(pfa,'SignalType','NonfluctuatingCoherent');

scatter(SNRdB,pd,max(SNRdB,1),'filled')

title('Receiver Operating Characteristic (ROC)')
xlabel('SNR (dB)')
ylabel('P_d')
grid on
title(legend('10^{-6}','10^{-4}'),'P_{fa}')

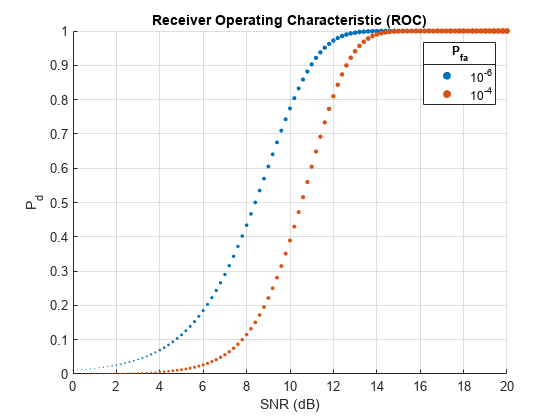
Figure contains an axes object. The axes object with title Receiver Operating Characteristic (ROC), xlabel SNR (dB), ylabel P indexOf d baseline P_d contains 2 objects of type scatter. These objects represent 10^{-6}, 10^{-4}.

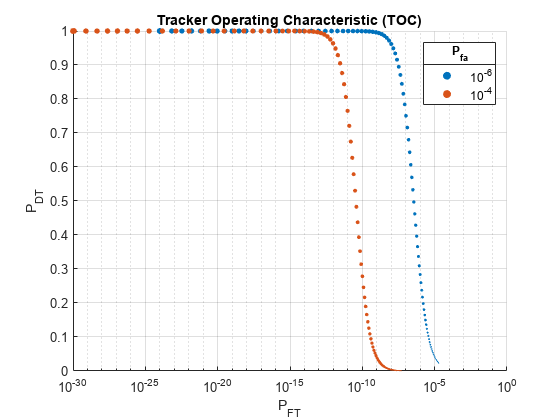
Compute the TOC curves using the probabilities of detection and probabilities of false alarm that you obtained. As the SNR increases, the probability of a false track in the presence of target detection increases. As the SNR decreases, the probability of target detection decreases, thereby increasing the probability of a false track.

[pct,pcf] = toccgh(pd.',pfa);

scatter(pcf,pct,max(SNRdB,1),'filled')

set(gca,'XScale','log')
title('Tracker Operating Characteristic (TOC)')
xlabel('P_{FT}')
ylabel('P_{DT}')
grid on
title(legend('10^{-6}','10^{-4}'),'P_{fa}')

Figure contains an axes object. The axes object with title Tracker Operating Characteristic (TOC), xlabel P indexOf FT baseline, ylabel P indexOf DT baseline contains 2 objects of type scatter. These objects represent 10^{-6}, 10^{-4}.

Input Arguments

collapse all

Probability of detection, specified as a vector or a matrix of values in the range [0, 1].

  • If pd is a vector, then it must have the same number of elements as pfa

  • If pd is a matrix, then its number of rows must equal the number of elements of pfa. In that case, the number of columns of pd equals the length of the signal-to-noise (SNR) ratio input to rocsnr or output by rocpfa.

Note

If you use rocpfa to obtain pd, you must transpose the output before using it as input to toccgh. If you use rocsnr to obtain pd, you do not have to transpose the output.

Example: [pd,pfa] = rocsnr(6) returns single-pulse detection probabilities and false-alarm probabilities for a coherent receiver with a nonfluctuating target and a signal-to-noise ratio of 6 dB.

Data Types: double

Probability of false alarm per cell (bin), specified as a vector of values in the range [0, 1].

Tip

Use pfa values of 10–3 or smaller to satisfy the assumptions of the common gate history algorithm.

Example: [pd,pfa] = rocsnr(6) returns single-pulse detection probabilities and false-alarm probabilities for a coherent receiver with a nonfluctuating target and a signal-to-noise ratio of 6 dB.

Data Types: double

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'UpdateTime',0.25,'MaximumAcceleration',8 specifies that the 1-D constant-velocity track Kalman filter used to compute the track gate growth has an update time of 0.25 second and a maximum acceleration of targets of interest of 8 meters per square second.

Confirmation threshold, specified as a two-element row vector of positive integers or a scalar. The two-element vector [M N] corresponds to an M-out-of-N or M/N confirmation logic, a test that stipulates that an event must occur at least M times in N consecutive updates.

  • A track is confirmed if there are at least M detections in N updates.

  • A track is deleted if there are less than M detections in N updates.

If this argument is specified as a scalar, toccgh treats it as a two-element vector with identical elements. N cannot be larger than 50.

Data Types: double

Number of cells, specified as a positive integer scalar. Use this argument to compute the expected number of false tracks.

Data Types: double

Number of targets, specified as a positive integer scalar. Use this argument to compute the expected number of false tracks.

Data Types: double

Update time for the default one-dimensional constant-velocity Kalman filter, specified as a positive scalar in seconds. This argument impacts the track gate growth.

Data Types: double

Maximum acceleration of targets of interest, specified as a nonnegative scalar in meters per square second. Use this input to tune the process noise in the default one-dimensional constant-velocity Kalman filter. This argument impacts the track gate growth.

Data Types: double

Range and range-rate resolution, specified as a two-element row vector of positive values. The first element of 'Resolution' is the range resolution in meters. The second element of 'Resolution' is the range rate resolution in meters per second. This argument is used to convert the predicted tracker gate size to bins.

Data Types: double

Tracker gate growth sequence, specified as a vector of positive integers. The values in the vector represent gate sizes in bins corresponding to N possible misses in N updates, where N is specified using 'ConfirmationThreshold'. If 'ConfirmationThreshold' is a two-element vector, then N is the second element of the vector.

If this argument is not specified, toccgh generates the tracker gate growth sequence using a one-dimensional constant-velocity Kalman filter implemented as a trackingKF object with these settings:

  • Update time — 0.5 second

  • Maximum target acceleration — 10 meters per square second

  • Range resolution — 1 meter

  • Range rate resolution — 1 meter per second

  • StateTransitionModel — [1 dt; 0 1], where dt is the update time

  • StateCovariance — [0 0; 0 0], which means the initial state is known perfectly

  • MeasurementNoise — 0

  • ProcessNoise — [dt^4/4 dt^3/2; dt^3/2 dt^2]*q, where dt is the update time, the tuning parameter q is amax^2*dt, and amax is the maximum acceleration. The tuning parameter is given in Equation 1.5.2-5 of [2].

To compute the gate sizes, the algorithm:

  1. Uses the predict function to compute the predicted state error covariance matrix.

  2. Calculates the area of the error ellipse as π times the product of the square roots of the eigenvalues of the covariance matrix.

  3. Divides the area of the error ellipse by the bin area to express the gate size in bins. The bin area is the product of the range resolution and the range rate resolution.

If this argument is specified, then the 'UpdateTime', 'MaxAcceleration', and 'Resolution' arguments are ignored.

Example: [21 39 95 125 155 259 301] specifies a tracker grate growth sequence that occurs on some radar applications.

Data Types: double

Output Arguments

collapse all

Probability of true target track in the presence of false alarms, returned as a matrix. pdt has the same size as pd.

Probability of false alarm track in the presence of targets, returned as a matrix. pft has the same size as pd.

Expected number of false tracks, returned as a matrix of the same size as pd. toccgh computes the expected number of tracks using

Eft=Pft,ntNc+PftNt,

where Pft,nt is the probability of false track in the absence of targets, Nc is the number of resolution cells specified in 'NumCells', Pft is the probability of false track in the presence of targets, and Nt is the number of targets specified in 'NumTargets'.

More About

collapse all

Common Gate History Algorithm

The common gate history (CGH) algorithm was developed by Bar-Shalom and collaborators and published in [1]. For more information about the CGH algorithm, see Assessing Performance with the Tracker Operating Characteristic.

The algorithm proceeds under these assumptions:

  • A track is one of these:

    1. Detections from targets only

    2. Detections from false alarms only

    3. Detections from targets and from false alarms

  • The probability of more than one false alarm in a gate is low, which is true when the probability of false alarm Pfa is low (Pfa ≤ 10–3).

  • The location of a target in a gate obeys a uniform spatial distribution.

The algorithm sequentially generates the gate history vector ω = [ωl, ωlt, λ], where:

  • ωl is the number of time steps since the last detection, either of a target or of a false alarm.

  • ωlt is the number of time steps since the last detection of a target.

  • λ is the number of detections.

The state vector evolves as a Markov chain by means of these steps:

  1. The algorithm initially creates a track. Only two events can initialize a track:

    • A target detection

    • A false alarm

  2. There are only four types of events that continue a track:

    • A1 — No detection

      Events of Type 1 occur with probability

      P{A1}=(1−g(ωl)g(ωlt)Pd)(1−Pfa)g(ωl)

      where Pd is the probability of detection specified using pd, Pfa is the probability of false alarm specified using pfa, g(ωl) is the gate size at step ωl, and g(ωlt) is the gate size at step ωlt.

      Note

      To reduce Pd to a lower effective value, toccgh weights it with the ratio

      g(ωl)g(ωlt)=Actual gate sizeSize of gate taking into account the time elapsed since the last target detection,

      which assumes a uniform spatial distribution of the location of a target in a gate. The gate sizes are specified using 'GateGrowthSequence'.

      Events of Type 1 update the gate history vector as [ωl, ωlt, λ] ➔ [ωl + 1, ωlt + 1, λ].

    • A2 — Target detection

      Events of Type 2 occur with probability

      P{A2}=g(ωl)g(ωlt)Pd(1−Pfa)g(ωl)

      and update the gate history vector as [ωl, ωlt, λ] ➔ [1, 1, λ + 1].

    • A3 — False alarm

      Events of Type 3 occur with probability

      P{A3}=(1−(1−Pfa)g(ωl))(1−g(ωl)g(ωlt)Pd)

      and update the gate history vector as [ωl, ωlt, λ] ➔ [1, ωlt + 1, λ + 1].

    • A4 — Target detection and false alarm

      Events of Type 4 occur with probability

      P{A4}=(1−(1−Pfa)g(ωl))(g(ωl)g(ωlt)Pd)

      and cause the track to split into a false track and a true track:

      • As,2a — Continue with A3, updating [ωl, ωlt, λ] ➔ [1, ωlt + 1, λ + 1].

      • As,2b — Continue with A2, updating [ωl, ωlt, λ] ➔ [1, 1, λ + 1].

    At each step, the algorithm multiplies each track probability by the probability of the event that continues the track.

  3. The procedure then lumps together the tracks that have a common gate history vector ω by adding their probabilities:

    • Tracks continued with A4 are lumped with tracks that continue with A3 (one false alarm only).

    • Tracks continued with A4 are lumped with tracks that continue with A2 (target detection only).

    This step controls the number of track states within the Markov chain.

At the end, the algorithm computes and assigns the final probabilities:

  • A target track is a sequence of detections that satisfies the M/N confirmation logic and contains at least one detection from a target. To compute the probability of target track:

    1. Determine the sequences that satisfy the confirmation logic under the assumption As,2b that A4 yields A2.

    2. Separately store these probabilities.

  • To compute the probability of false track:

    1. Compute the probability of target track under the assumption As,2a that A4 yields A3.

    2. Subtract this probability from the probability of all detection sequences that satisfy the confirmation logic.

References

[1] Bar‐Shalom, Yaakov, Leon J. Campo, and Peter B. Luh. "From Receiver Operating Characteristic to System Operating Characteristic: Evaluation of a Track Formation System." IEEE® Transactions on Automatic Control 35, no. 2 (February 1990): 172–79. https://doi.org/10.1109/9.45173.

[2] Bar-Shalom, Yaakov, Peter K. Willett, and Xin Tian. Tracking and Data Fusion: A Handbook of Algorithms. Storrs, CT: YBS Publishing, 2011.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Version History

Introduced in R2021a

See Also

|

Topics