Design, Visualize and Explore Inverse Chebyshev Filter - II

This example uses:

This example shows how to design a fourth-order inverse Chebyshev low-pass filter with stopband frequency of 10000 rad/sec, and epsilon of 0.01 (please see the reference section) using rffilter. This rffilter could be used in a circuit or in a rfbudget object.

The rffilter object is used to design a RF filter. A filter requires a minimum set for parameters to completely define it.

The parameters to design an inverse Chebyshev filter can be one of the following:

Filter order, Passband frequency, Passband and Stopband Attenuation
Passband and Stopband frequencies, Passband and Stopband Attenuation
Filter order, Stopband frequency, Stopband Attenuation

Design Filter

N           = 4;                                    % Filter order
Fs          = 1000/(2*pi);                          % Stopband frequency
epsilon     = 0.01;             
Rs          = 10*log10((1+epsilon^2)/epsilon^2);    % Stopband attenuation

Use the first set of parameters to define the filter.

r = rffilter('FilterType','InverseChebyshev','ResponseType','Lowpass',  ...
    'Implementation','Transfer function','FilterOrder',N,               ...
    'PassbandFrequency',Fs,'PassbandAttenuation',Rs,                    ...
    'StopbandAttenuation',Rs);

Note: Alternative, you can also use the third set of parameters to design the same filter:

r = rffilter('FilterType','InverseChebyshev','ResponseType','Lowpass',  ...
'Implementation','Transfer function','FilterOrder',N,                   ...
'StopbandFrequency',Fs,'StopbandAttenuation',Rs);

The limitation of this parameter set is that it assumes the passband attenuation to be fixed at 10*log10(2) dB.

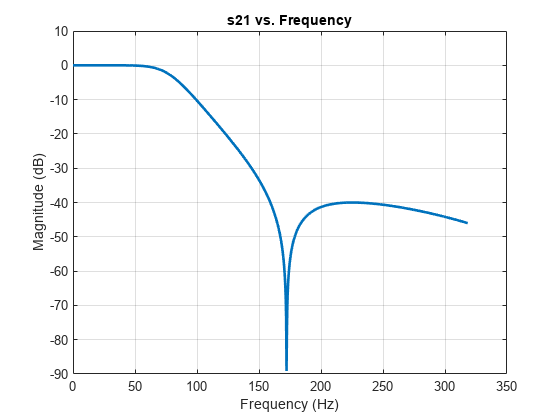
Visualize magnitude response, phase response, and phase delay of filter

frequencies = linspace(0,2*Fs,1001);
rfplot(r, frequencies);

Figure S-Parameters 21 contains an axes object and another object of type uitoolbar. The axes object with title s21 vs. Frequency, xlabel Frequency (Hz), ylabel Magnitude (dB) contains an object of type line.

Optionally, you can also use Signal Processing Toolbox to visualize the analog filter using:

freqs(numerator{2,1},denominator)

Find zeros, poles, and gain

[z,p,k] = zpk(r);

You can obtain zeros, poles, and gain of Transfer function (S21) by:

format long g
zeros_21 = z{2,1}

zeros_21 = 4×1 complex

                          0 +      1082.39220029239i
                          0 -      1082.39220029239i
                          0 +      2613.12592975275i
                          0 -      2613.12592975275i

poles_21 = p                % Same denominator for S11, S12, S21 and S22

poles_21 = 4×1 complex

          -171.158733950657 +      476.096694464131i
          -171.158733950657 -      476.096694464131i
          -504.530434776367 +      240.786480832184i
          -504.530434776367 -      240.786480832184i

k_21     = k{2,1}

k_21 = 
       0.00999950003749688

View transfer function in factorized form

View these factor forms directly from the filter r.

disp('Numerator of Transfer function as factors:');

Numerator of Transfer function as factors:

r.DesignData.Numerator21

ans = 2×3

                         1                         0          1171572.87525381
       0.00999950003749688                         0          68280.8572899443

disp('Denominator of Transfer function as factors:');

Denominator of Transfer function as factors:

r.DesignData.Denominator

ans = 2×3

                         1          342.317467901314          255963.374687264
                         1          1009.06086955273          312529.088967178

Alternatively, use |zpk| from Control System Toolbox to view the transfer function in factorized form.

G_s = zpk(zeros_21,poles_21,k_21)

G_s =
 
     0.0099995 (s^2 + 1.172e06) (s^2 + 6.828e06)
  -------------------------------------------------
  (s^2 + 1009s + 3.125e05) (s^2 + 342.3s + 2.56e05)
 
Continuous-time zero/pole/gain model.

References

[1] Paarmann, L. D. Design and Analysis of Analog Filters: A Signal Processing Perspective. SECS 617. Boston: Kluwer Academic Publishers, 2001.