Fault-Tolerant Control of a Passenger Jet

Background

This example deals with fault-tolerant flight control of a passenger jet undergoing outages in the elevator and aileron actuators. The flight control system must maintain stability and meet performance and comfort requirements in both nominal operation and degraded conditions where some actuators are no longer effective due to control surface impairment. Wind gusts must be alleviated in all conditions. This application is sometimes called reliable control as aircraft safety must be maintained in extreme flight conditions.

Aircraft Model

The control system is modeled in Simulink®.

open_system('faultTolerantAircraft')

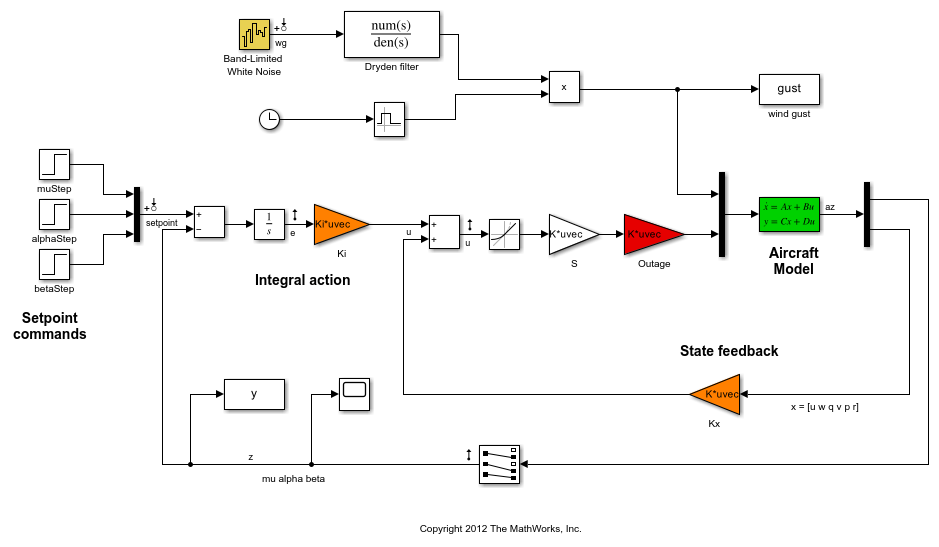
The aircraft is modeled as a rigid 6th-order state-space system with the following state variables (units are mph for velocities and deg/s for angular rates):

The state vector is available for control as well as the flight-path bank angle rate mu (deg/s), the angle of attack alpha (deg), and the sideslip angle beta (deg). The control inputs are the deflections of the right elevator, left elevator, right aileron, left aileron, and rudder. All deflections are in degrees. Elevators are grouped symmetrically to generate the angle of attack. Ailerons are grouped anti-symmetrically to generate roll motion. This leads to 3 control actions as shown in the Simulink model.

The controller consists of state-feedback control in the inner loop and MIMO integral action in the outer loop. The gain matrices Ki and Kx are 3-by-3 and 3-by-6, respectively, so the controller has 27 tunable parameters.

Actuator Failures

We use a 9x5 matrix to encode the nominal mode and various actuator failure modes. Each row corresponds to one flight condition, a zero indicating outage of the corresponding deflection surface.

OutageCases = [...
   1 1 1 1 1; ... % nominal operational mode
   0 1 1 1 1; ... % right elevator outage
   1 0 1 1 1; ... % left elevator outage
   1 1 0 1 1; ... % right aileron outage
   1 1 1 0 1; ... % left aileron outage
   1 0 0 1 1; ... % left elevator and right aileron outage
   0 1 0 1 1; ... % right elevator and right aileron outage
   0 1 1 0 1; ... % right elevator and left aileron outage
   1 0 1 0 1; ... % left elevator and left aileron outage
   ];

Design Requirements

The controller should:

To express the first requirement, you can use an LQG-like cost function that penalizes the integrated tracking error e and the control effort u:

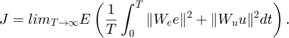
The diagonal weights 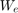and 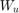are the main tuning knobs for trading responsiveness and control effort and emphasizing some channels over others. Use the WeightedVariance requirement to express this cost function, and relax the performance weight 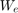by a factor 2 for the outage scenarios.

We = diag([10 20 15]);   Wu = eye(3);

% Nominal tracking requirement
SoftNom = TuningGoal.WeightedVariance('setpoint',{'e','u'}, blkdiag(We,Wu), []);
SoftNom.Models = 1;    % nominal model

% Tracking requirement for outage conditions
SoftOut = TuningGoal.WeightedVariance('setpoint',{'e','u'}, blkdiag(We/2,Wu), []);
SoftOut.Models = 2:9;  % outage scenarios

For wind gust alleviation, limit the variance of the error signal e due to the white noise wg driving the wind gust model. Again use a less stringent requirement for the outage scenarios.

% Nominal gust alleviation requirement
HardNom = TuningGoal.Variance('wg','e',0.02);
HardNom.Models = 1;

% Gust alleviation requirement for outage conditions
HardOut = TuningGoal.Variance('wg','e',0.1);
HardOut.Models = 2:9;

Controller Tuning for Nominal Flight

Set the wind gust speed to 10 mph and initialize the tunable state-feedback and integrators gains of the controller.

GustSpeed = 10;
Ki = eye(3);
Kx = zeros(3,6);

Use the slTuner interface to set up the tuning task. List the blocks to be tuned and specify the nine flight conditions by varying the outage variable in the Simulink model. Because you can only vary scalar parameters in slTuner, independently specify the values taken by each entry of the outage vector.

OutageData = struct(...
   'Name',{'outage(1)','outage(2)','outage(3)','outage(4)','outage(5)'},...
   'Value',mat2cell(OutageCases,9,[1 1 1 1 1]));
ST0 = slTuner('faultTolerantAircraft',{'Ki','Kx'},OutageData);

Use systune to tune the controller gains subject to the nominal requirements. Treat the wind gust alleviation as a hard constraint.

[ST,fSoft,gHard]  = systune(ST0,SoftNom,HardNom);

Final: Soft = 22.6, Hard = 0.99905, Iterations = 287

Retrieve the gain values and simulate the responses to step commands in mu, alpha, beta for the nominal and degraded flight conditions. All simulations include wind gust effects, and the red curve is the nominal response.

Ki = getBlockValue(ST, 'Ki');  Ki = Ki.d;
Kx = getBlockValue(ST, 'Kx');  Kx = Kx.d;

% Bank-angle setpoint simulation
plotResponses(OutageCases,1,0,0);

% Angle-of-attack setpoint simulation
plotResponses(OutageCases,0,1,0);

% Sideslip-angle setpoint simulation
plotResponses(OutageCases,0,0,1);

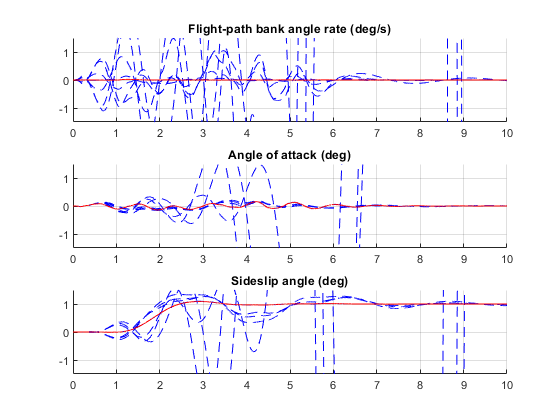
The nominal responses are good but the deterioration in performance is unacceptable when faced with actuator outage.

Controller Tuning for Impaired Flight

To improve reliability, retune the controller gains to meet the nominal requirement for the nominal plant as well as the relaxed requirements for all eight outage scenarios.

[ST,fSoft,gHard]  = systune(ST0,[SoftNom;SoftOut],[HardNom;HardOut]);

Final: Soft = 25.7, Hard = 0.999, Iterations = 520

The optimal performance (square root of LQG cost 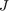) is only slightly worse than for the nominal tuning (26 vs. 23). Retrieve the gain values and rerun the simulations (red curve is the nominal response).

Ki = getBlockValue(ST, 'Ki');  Ki = Ki.d;
Kx = getBlockValue(ST, 'Kx');  Kx = Kx.d;

% Bank-angle setpoint simulation
plotResponses(OutageCases,1,0,0);

% Angle-of-attack setpoint simulation
plotResponses(OutageCases,0,1,0);

% Sideslip-angle setpoint simulation
plotResponses(OutageCases,0,0,1);

The controller now provides acceptable performance for all outage scenarios considered in this example. The design could be further refined by adding specifications such as minimum stability margins and gain limits to avoid actuator rate saturation.