Main Content

robgain

Robust performance of uncertain system

collapse all in page

Syntax

[perfmarg,wcu] = robgain(usys,gamma)
[perfmarg,wcu] = robgain(usys,gamma,w)
[perfmarg,wcu] = robgain(___,opts)
[perfmarg,wcu,info] = robgain(___)

Description

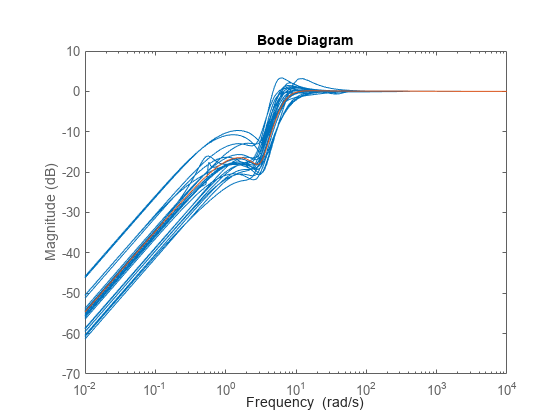
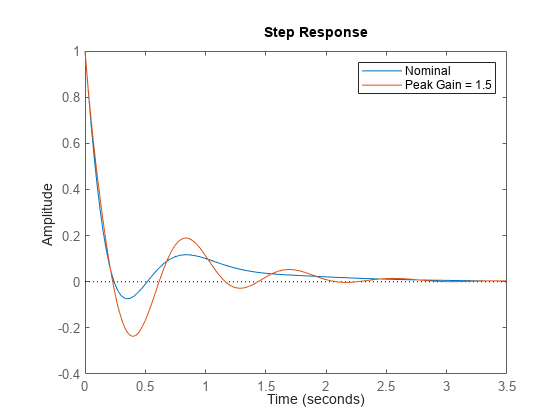
[perfmarg,wcu] = robgain(usys,gamma) calculates the robust performance margin for an uncertain system and the performance level gamma. The performance of usys is measured by its peak gain or peak singular value (see Robustness and Worst-Case Analysis). The performance margin is relative to the uncertainty level specified in usys. A margin greater than 1 means that the gain of usys remains below gamma for all values of the uncertainty modeled in usys. A margin less than 1 means that at some frequency, the gain of usys exceeds gamma for some values of the uncertain elements within their specified ranges. For example, a margin of 0.5 implies the following:

  • The gain of usys remains below gamma as long as the uncertain element values stay within 0.5 normalized units of their nominal values.

  • There is a perturbation of size 0.5 normalized units that drives the peak gain to the level gamma.

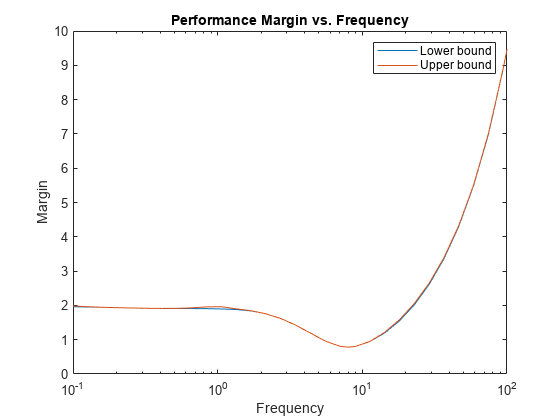
The structure perfmarg contains upper and lower bounds on the actual performance margin and the critical frequency at which the margin upper bound is smallest. The structure wcu contains the uncertain-element values that drive the peak gain to the level gamma.

example

[perfmarg,wcu] = robgain(usys,gamma,w) assesses the robust performance margin for the frequencies specified by w.

  • If w is a cell array of the form {wmin,wmax}, then robgain restricts the performance margin computation to the interval between wmin and wmax.

  • If w is a vector of frequencies, then robgain computes the performance margin at the specified frequencies only.

example

[perfmarg,wcu] = robgain(___,opts) specifies additional options for the computation. Use robOptions to create opts. You can use this syntax with any of the previous input-argument combinations.

example

[perfmarg,wcu,info] = robgain(___) returns a structure with additional information about the performance margins and the perturbations that drive the gain to gamma. See info for details about this structure. You can use this syntax with any of the previous input-argument combinations.

Examples

collapse all

Open Live Script

Consider a control system whose plant contains both parametric uncertainty and dynamic uncertainty. Create a model of the plant using uncertain elements.

k = ureal('k',10,'Percent',40);
delta = ultidyn('delta',[1 1]); 
G = tf(18,[1 1.8 k]) * (1 + 0.5*delta);

Create a model of the controller, and build the closed-loop sensitivity function, S. The sensitivity measures the closed-loop response at the plant output to a disturbance at the plant input.

C = pid(2.3,3,0.38,0.001);
S = feedback(1,G*C);
bodemag(S,S.NominalValue)

MATLAB figure

The peak gain of the nominal response is very nearly 1, but some of the sampled systems within the uncertainty range exceed that level. Suppose that you can tolerate some ringdown in the response but do not want the peak gain to exceed 1.5. Use robgain to find out how much uncertainty the system can have while the peak gain remains below 1.5.

[perfmarg,wcu] = robgain(S,1.5);
perfmarg
perfmarg = struct with fields:
           LowerBound: 0.7821
           UpperBound: 0.7837
    CriticalFrequency: 7.8566

The LowerBound and UpperBound fields of perfmarg show that the robust performance margin is around 0.78. This result means that there is a perturbation of only about 78% of the uncertainty specified in S with peak gain exceeding 1.5.

You can use uscale to examine what that normalized uncertainty of 78% means in terms of actual ranges of uncertainty. Scale all the uncertain elements in S to create a model of the closed-loop system with the maximum level of uncertainty that meets the performance requirement. 

factor = perfmarg.LowerBound;
S_scaled = uscale(S,factor)
Uncertain continuous-time state-space model with 1 outputs, 1 inputs, 4 states.
The model uncertainty consists of the following blocks:
  delta: Uncertain 1x1 LTI, peak gain = 0.782, 1 occurrences
  k: Uncertain real, nominal = 10, variability = [-31.3,31.3]%, 1 occurrences

Type "S_scaled.NominalValue" to see the nominal value and "S_scaled.Uncertainty" to interact with the uncertain elements.

The display shows how the uncertain elements in S_scaled have changed: the peak gain of the ultidyn element delta is reduced from 1 to 0.78, and the range of variation of the uncertain real parameter k is reduced from ±40% to ±31.3%.

The output wcu is a structure that contains the perturbations to k and delta that correspond to the target maximum performance of 1.5. Verify that the values in wcu cause Smax to achieve the gain level of 1.5 by substituting them into S.

Smax = usubs(S,wcu);
getPeakGain(Smax,1e-6)
ans = 
1.5001

Examine the disturbance rejection of the system with these values.

step(S.NominalValue,Smax)
legend('Nominal','Peak Gain = 1.5')

MATLAB figure

The CriticalFrequency field of perfmarg contains the frequency at which the peak gain reaches 1.5.

Open Live Script

Examine the relative sensitivity of the robust performance margin to the uncertain elements of the system. Consider a model of a control system containing uncertain elements.

k = ureal('k',10,'Percent',50);
delta = ultidyn('delta',[1 1]); 
G = tf(18,[1 1.8 k]) * (1 + 0.15*delta);
C = pid(2.3,3,0.38,0.001);
S = feedback(1,G*C);

Create an options set for robgain that enables the sensitivity calculation.

opts = robOptions('Sensitivity','On');

Calculate the robust performance margin of the system relative to a peak gain of 1.5, specifying the info output to access additional information about the calculation.

[perfmarg,wcu,info] = robgain(S,1.5,opts);

Examine the Sensitivity field of info.

info.Sensitivity
ans = struct with fields:
    delta: 75
        k: 28

The values in this field indicate how much a change in the normalized perturbation on each element affects the performance margin. For example, the sensitivity for k is 28. This value means that a given change dk in the normalized uncertainty range of k causes a change of about 28% of that, or 0.28*dk, in the performance margin. The margin in this case is more sensitive to delta, for which the margin changes by about 75% of the change in the normalized uncertainty range.

Open Live Script

Consider a model of a control system containing uncertain elements. 

k = ureal('k',10,'Percent',40);
delta = ultidyn('delta',[1 1]); 
G = tf(18,[1 1.8 k]) * (1 + 0.5*delta);
C = pid(2.3,3,0.38,0.001);
S = feedback(1,G*C);

By default, robgain computes only the weakest performance margin over all frequencies. To see how the margin varies with frequency, use the 'VaryFrequency' option of robOptions. For example, compute the performance margin of the system for a performance level of 1.5, at frequency points between 0.1 and 100 rad/s.

opts = robOptions('VaryFrequency','on');
[perfmarg,wcu,info] = robgain(S,1.5,{0.1,100},opts);
info
info = struct with fields:
                Model: 1
            Frequency: [32x1 double]
               Bounds: [32x2 double]
    WorstPerturbation: [32x1 struct]
          Sensitivity: [1x1 struct]

robgain returns the vector of frequencies in the info output, in the Frequencies field. info.Bounds contains the upper and lower bounds on the performance margin at each frequency. Use these values to plot the frequency dependence of the performance margin.

semilogx(info.Frequency,info.Bounds)
title('Performance Margin vs. Frequency')
ylabel('Margin')
xlabel('Frequency')
legend('Lower bound','Upper bound')

Figure contains an axes object. The axes object with title Performance Margin vs. Frequency, xlabel Frequency, ylabel Margin contains 2 objects of type line. These objects represent Lower bound, Upper bound.

When you use the 'VaryFrequency' option, robgain chooses frequency points automatically. The frequencies it selects are guaranteed to include the frequency at which the margin is smallest (within the specified range). Display the returned frequency values to confirm that they include the critical frequency.

info.Frequency
ans = 32×1

    0.1000
    0.1266
    0.1604
    0.2031
    0.2572
    0.3257
    0.4125
    0.5223
    0.6615
    0.8377
      ⋮


perfmarg.CriticalFrequency
ans = 
7.9966

Alternatively, instead of using 'VaryFrequency', you can specify particular frequencies at which to compute the robust performance margins. info.Bounds contains the margins at all specified frequencies. However, these results are not guaranteed to include the weakest margin, which might fall between specified frequency points.

w = logspace(-1,2,20); 
[perfmarg,wcu,info] = robgain(S,1.5,w);
semilogx(w,info.Bounds)
title('Performance Margin vs. Frequency')
ylabel('Margin')
xlabel('Frequency')
legend('Lower bound','Upper bound')

Figure contains an axes object. The axes object with title Performance Margin vs. Frequency, xlabel Frequency, ylabel Margin contains 2 objects of type line. These objects represent Lower bound, Upper bound.

Input Arguments

collapse all

Dynamic system with uncertainty, specified as a uss, ufrd, genss, or genfrd model that contains uncertain elements. For genss or genfrd models, robgain uses the current value of any tunable blocks and folds them into the known (not uncertain) part of the model.

usys can also be an array of uncertain models. In that case, robgain returns the smallest margin across all models in the array, and the info output contains the index of the corresponding model.

Performance level, specified as a positive scalar. The performance level is the peak gain of a system or, for MIMO systems, the peak singular value (H∞ norm). Generally, the lower this value, the better the system performance. robgain computes the amount of uncertainty the system can tolerate while keeping the peak gain below this level. For more information about this performance measure, see Robustness and Worst-Case Analysis.

Frequencies at which to compute robust performance margins, specified as the cell array {wmin,wmax} or as a vector of frequency values.

  • If w is a cell array of the form {wmin,wmax}, then the function computes the margins at frequencies ranging between wmin and wmax.

  • If w is a vector of frequencies, then the function computes the margins at each specified frequency. For example, use logspace to generate a row vector with logarithmically spaced frequency values.

Specify frequencies in units of rad/TimeUnit, where TimeUnit is the TimeUnit property of the model.

Options for computation of robust performance margins, specified as an object you create with robOptions. The available options include settings that let you:

  • Extract frequency-dependent performance margins.

  • Examine the sensitivity of the margins to each uncertain element.

  • Improve the results of the performance-margin calculation by setting certain options for the underlying mussv calculation. In particular, setting the option 'MussvOptions' to 'mN' can reduce the gap between the lower bound and upper bound. N is the number of restarts.

For more information about all available options, see robOptions.

Example: robOptions('Sensitivity','on','MussvOptions','m3')

Output Arguments

collapse all

Robust performance margin and critical frequency, returned as a structure containing the following fields:

FieldDescription

LowerBound

Lower bound on the actual robust performance margin of the model with respect to gamma, returned as a scalar value. The exact margin is guaranteed to be no smaller than LowerBound. In other words, for all modeled uncertainty with normalized magnitude up to LowerBound, the system is guaranteed to have peak gain below gamma.

UpperBound

Upper bound on the actual robust performance margin, returned as a scalar value. The exact margin is guaranteed to be no larger than UpperBound. In other words, there exist some uncertain-element values associated with this magnitude that drive the peak gain above gamma. robgain returns one such instance in wcu.

CriticalFrequency

Frequency at which the performance margin is the smallest, in rad/TimeUnit, where TimeUnit is the TimeUnit property of usys.

A margin greater than 1 means that the gain of usys remains below gamma for all values of the uncertainty modeled in usys. A margin less than 1 means that at some frequency, the gain of usys exceeds gamma for some values of the uncertain elements within their specified ranges. For example, a margin of 0.5 implies the following:

  • The gain of usys remains below gamma as long as the uncertain element values stay within 0.5 normalized units of their nominal values.

  • There is a perturbation of size 0.5 normalized units that drives the peak gain above gamma.

Use uscale to scale the amount of uncertainty in usys by the performance margin to examine the actual ranges of uncertainty that yield the target performance.

If the nominal value of usys has peak gain greater than gamma, the performance margin is 0.

If usys is an array of uncertain models, perfmarg contains the smallest margin across all models in the array. In that case, the info output contains the index of the corresponding model in its Model field.

Smallest perturbations of uncertain elements that drive the peak gain of usys to the level gamma, returned as a structure whose fields are the names of the uncertain elements of usys. Each field contains the actual value of the corresponding uncertain element. For example, if usys includes an uncertain matrix M and SISO uncertain dynamics delta, then wcu.M is a numeric matrix and wcu.delta is a SISO state-space model.

Use usubs(usys,wcu) to substitute these values for the uncertain elements in usys and obtain the corresponding dynamic system. This system has peak gain gamma.Use actual2normalized to convert these actual uncertainty values to the normalized units in which the performance margin is expressed.

For ureal parameters in usys whose range is not centered around the nominal value, robgain makes the following adjustments for the purposes of its analysis:

  • When the worst perturbation (the smallest perturbation achieving target gain) lies outside the range of validity of the actual-to-normalized transformation (see getLimits), then robgain sets the corresponding entry of wcu to the nearest valid value. In other words, if actpert is the worst perturbation in actual units, robgain sets wcu to the nearest value inside the interval ActLims returned by getLimits.

  • When there is no perturbation causing the system to exceed the target gain, then robgain sets the corresponding entry of wcu to the nominal value of the ureal parameter.

Additional information about the performance margins, returned as a structure with the following fields:

FieldDescription

Model

Index of the model that has the weakest performance margin, when usys is an array of models.

Frequency

Frequency points at which robgain returns the robust performance margin, returned as a vector.

  • If the 'VaryFrequency' option of robOptions is 'off', then info.Frequency is the critical frequency, the frequency at which the smallest margin occurs. If the smallest lower bound and the smallest upper bound on the performance margin occur at different frequencies, then info.Frequency is a vector containing these two frequencies.

  • If the 'VaryFrequency' option of robOptions is 'on', then info.Frequency contains the frequencies selected by robgain. These frequencies are guaranteed to include the frequency at which the performance margin is smallest.

  • If you specify a vector of frequencies w at which to compute the performance margins, then info.Frequency = w. When you specify a frequency vector, these frequencies are not guaranteed to include the frequency at which the margin is smallest.

The 'VaryFrequency' option is meaningful only for uss and genss models. robgain ignores the option for ufrd and genfrd models.

Bounds

Lower and upper bounds on the actual robust performance margin of the model, returned as an array. info.Bounds(:,1) contains the lower bound at each corresponding frequency in info.Frequency, and info.Bounds(:,2) contains the corresponding upper bounds.

WorstPerturbation

Smallest perturbations at each frequency point in info.Frequency, returned as a structure array. The fields of info.WorstPerturbation are the names of the uncertain elements in usys. Each field contains the value of the corresponding element that drives the peak gain above gamma at each frequency. For example, if usys includes an uncertain parameter p and SISO uncertain dynamics delta, then info.WorstPerturbation.p is a collection of numeric values and info.WorstPerturbation.delta is a collection of SISO state-space models.

Sensitivity

Sensitivity of the performance margin to each uncertain element, returned as a structure when the 'Sensitivity' option of robOptions is 'on'. The fields of info.Sensitivity are the names of the uncertain elements in usys. Each field contains a percentage that measures how much the uncertainty in the corresponding element affects the performance margin. For example, if info.Sensitivity.p is 50, then a given fractional change in the uncertainty range of p causes half as much fractional change in the performance margin.

If the 'Sensitivity' option of robOptions is off (the default setting), then info.Sensitivity is NaN.

Algorithms

Computing the robustness margin at a particular frequency is equivalent to computing the structured singular value, μ, for some appropriate block structure (μ-analysis).

For uss and genss models, robgain(usys) and robgain(usys,{wmin,wmax}) use an algorithm that finds the smallest margin across frequency. This algorithm does not rely on frequency gridding and is not adversely affected by discontinuities of the μ structured singular value. See Getting Reliable Estimates of Robustness Margins for more information.

For ufrd and genfrd models, robgain computes the μ lower and upper bounds at each frequency point. This computation offers no guarantee between frequency points and can be inaccurate if there are discontinuities or sharp peaks in μ. The syntax robgain(uss,w), where w is a vector of frequency points, is the same as robgain(ufrd(uss,w)) and also relies on frequency gridding to compute the margin.

In general, the algorithm for state-space models is faster and safer than the frequency-gridding approach. In some cases, however, the state-space algorithm requires many μ calculations. In those cases, specifying a frequency grid as a vector w can be faster, provided that the robustness margin varies smoothly with frequency. Such smooth variation is typical for systems with dynamic uncertainty.

Version History

Introduced in R2016b

See Also

| | |

Topics