D-K Iteration Process

You can use the musyn command to design a robust controller for an uncertain plant, as described in Robust Controller Design Using Mu Synthesis. The algorithm used by musyn is an iterative process called D-K iteration. In this process, the function:

Uses H_∞ synthesis to find a controller that minimizes the closed-loop gain of the nominal system.
Performs a robustness analysis to estimate the robust H_∞ performance of the closed-loop system. This quantity is expressed as a scaled H_∞ norm involving dynamic scalings called the D and G scalings (the D step).
Finds a new controller to minimize the scaled H_∞ norm obtained in step 2 (the K step).
Repeats steps 2 and 3 until the robust performance stops improving.

Both the D step and K step are mathematically intensive computations. Details of the algorithm follow.

D Step

In the D step, musyn computes the upper bound $\bar{μ}$ of the robust H_∞ performance for the current controller K. The D step begins with a robust performance analysis for the closed-loop uncertain system T = LFT(P,K), as in the following diagram.

Closed-loop system T with inputs and output z. T consists of nominal system T_0 in LFT feedback configuration with an uncertain block Delta_unc. T_0 is a nominal plant P_0, having input w and output z, in an LFT feedback configuration with controller K.

Introducing a performance block Δ_perf transforms the robust-performance analysis of T to a robust-stability analysis of the feedback loop in the following diagram.

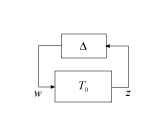
T_0 in LFT feedback configuration with block Delta.

Here, Δ is the augmented uncertainty structure

$Δ ≜ (\begin{matrix} Δ_{p e r f} & 0 \\ 0 & Δ_{u n c} \end{matrix}) .$

musyn computes $\bar{μ}$ , an upper bound on the robust H_∞ performance. To do so, musyn selects a frequency grid {ω₁,…,ω_N}. For T with complex uncertainty only, musyn computes at each frequency ω_i

${\bar{μ}}_{i} = \inf_{D_{i}} ‖ D_{i} T_{0} (j ω_{i}) D_{i}^{- 1} ‖ .$

The frequency-dependent matrices D, which commute with Δ, are called D scalings. $\bar{μ}$ is the largest result over all frequencies in the grid,

$\bar{μ} = \max_{i} {\bar{μ}}_{i} .$

When you use musyn, you can access the results of the D step in several ways.

The default musyn display shows $\bar{μ}$ for each iteration in the Peak MU column.
musyn returns $\bar{μ}$ for each iteration in the PeakMU field of the info output argument.
musyn returns D_i in the DG field of the info output argument.
To visualize the frequency-dependence of D_i, set the 'Display' option of musynOptions to 'full'.

For additional details about the computation and interpretation of $\bar{μ}$ , see Robust Performance Measure for Mu Synthesis.

D-Fitting and Scaled H_∞ Performance

musyn fits a rational function D(s) to the sequence of scalings {D_i}. The fit yields a quantity μ_F called the scaled H_∞ performance,

$μ_{F} ≜ {‖ D (T_{0}) D^{- 1} ‖}_{\infty} .$

Because the fit is not exact, μ_F is typically somewhat larger than $\bar{μ}$ .

You can access the results of the fit in several ways.

The default musyn display shows μ_F for each iteration in the DG Fit column.
musyn returns μ_F for each iteration in the PeakMUFit field of the info output argument.
musyn returns the fitting functions in the dr and dc fields of the info output argument.
To visualize the frequency dependence of the fitting functions, set the 'Display' option of musynOptions to 'full'.

K Step

T₀ depends on the choice of controller K by the relation T₀ = LFT(P₀,K). Therefore, minimizing μ_F with respect to K is a scaled H_∞ synthesis problem. Thus, in the K step, musyn uses hinfsyn or hinfstruct to compute a controller K^* that minimizes μ_F. The minimized quantity is the scaled H_∞ norm. For the algorithm to make progress, the new controller must improve the robust performance obtained in the D step:

${‖ D LFT (P_{0}, K^{*}) D^{- 1} ‖}_{\infty} < \bar{μ} .$

Otherwise, the progress is not sufficient for compensate for fitting errors. Thus musyn terminates D-K iteration process when K^* does not improve the robust performance within the tolerance specified by the 'TolPerf' option of musynOptions.

You can access the results of the K step in several ways.

The default musyn display shows the scaled H_∞ norm for each iteration in the K Step column.
musyn returns the new controller in the K of the info output argument, and the corresponding scaled H_∞ norm for each iteration in the gamma field.

Mixed Real and Complex Uncertainty

When the system has both real and complex uncertainty and you set the 'MixedMU' option of musynOptions to 'on', musyn uses an additional G-scaling to improve the computation of $\bar{μ}$ . The algorithm in this case is called mixed-μ synthesis.

For mixed uncertainty, musyn computes ${\bar{μ}}_{i}$ and scalings D_r(ω_i), D_c(ω_i), and G_cr(ω_i) such that

${(\begin{matrix} T_{0} (j ω_{i}) \\ I \end{matrix})}^{H} (\begin{matrix} D_{r} (ω_{i}) & - j G_{c r}^{H} (ω_{i}) \\ j G_{c r} (ω_{i}) & - {\bar{μ}}_{i}^{2} D_{c} (ω_{i}) \end{matrix}) (\begin{matrix} T_{0} (j ω_{i}) \\ I \end{matrix}) \leq 0$

at each frequency in the grid.

musyn fits the D and G scaling data by constructing a rational function

$F (s) = Ψ (s) (\begin{matrix} d_{r} (s) & 0 \\ 0 & d_{c} (s) \end{matrix})$

such that

d_r(s), d_c(s), and Ψ(s) are stable with stable inverse.
d_r(s) and d_c(s) approximate the square roots of the diagonal entries of D_r(ω_i) and D_c(ω_i).
F approximately satisfies
$\begin{matrix} (\begin{matrix} D_{r} (ω_{i}) & - j G_{c r}^{H} (ω_{i}) \\ j G_{c r} (ω_{i}) & - μ^{2} D_{c} (ω_{i}) \end{matrix}) \approx F {(j ω_{i})}^{H} J F (j ω_{i}), \\ J = (\begin{matrix} I_{r} & 0 \\ 0 & - I {}_{c} \end{matrix}) . \end{matrix}$

Finally, the scaled H_∞ performance is defined as

$μ_{F} ≜ {‖ \bar{T} (s) ‖}_{\infty},$

where $\bar{T} (s)$ is the transformed system,

$\bar{T} (s) ≜ \bar{μ} {\bar{T}}_{1} {\bar{T}}_{2}^{- 1}, (\begin{matrix} {\bar{T}}_{1} (s) \\ {\bar{T}}_{2} (s) \end{matrix}) ≜ Ψ (s) (\begin{matrix} d_{r} (s) T_{0} (s) \\ d_{c} (s) \end{matrix}) .$

For an exact fit of D and G, $‖ \bar{T} (j ω_{i}) ‖ = {\bar{μ}}_{i}$ . Therefore, in general, $μ_{F} \geq \bar{μ} .$

Because the transformed system $\bar{T} (s)$ is still a linear fractional function of the controller K, the K step for the mixed-μ case proceeds by computing a controller K* that minimizes ${‖ \bar{T} ‖}_{\infty}$ .

When using musyn, you can access the D and G scalings in several ways.

musyn returns the D and G scaling data in the DG field of the info output argument.
musyn returns the fitting functions in the dr, dc, and PSI fields of the info output argument.
To visualize the frequency dependence of the scaling data and fitting functions, set the 'Display' option of musynOptions to 'full'.